题目链接:https://vjudge.net/contest/241341#problem/C
题目大意:给你从1到n总共n个数字,同时给你n-1个连接,同时保证任意两个点之间都可以连接。现在假设任意两个点简单连通路过某点则某点的繁荣度+1,求所有点的最大繁荣度。
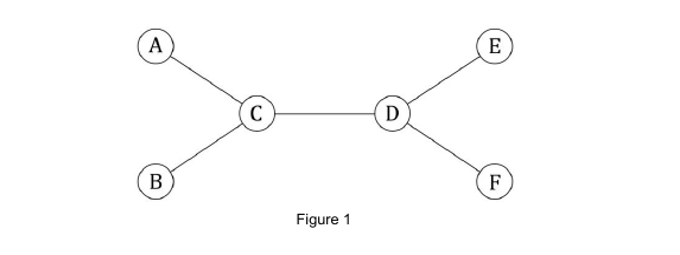
解题思路:以它为例,根据题意,对于C节点我们要计算它的繁荣度,一般大家都会的,肯定就是1*1+1*3+1*3=7;也就是说是以C为根节点的任意两颗子树节点个数的乘积的和,不过这样感觉好像很复杂啊,又要计算以每个节点为根节点的子树节点个数又还要把他们两个两个乘起来再相加,代码不好写不说,而且肯定会超时。
那该怎么做呢,这里需要转换思维了,任意一点的繁荣度应该等于:以它为根节点的每个子树节点个数乘以除这颗子树以及根节点外其它所有节点的和,即子树1*除去子树1和根节点个数+子树2*除去子树2和根节点的节点个数+……,依次类推,不过这样每个都乘了两次,所以算出的结果再除2就行了,这样就简单多了。
代码的实现:把整个图看成以1号节点为根的大树,用一个cnt数组来存储以当前节点个根节点形成的树的节点个数,然后写一个DFS,搜索树的各个子树的节点个数。
具体见代码:
1 #include<iostream>
2 #include<vector>
3 using namespace std;
4 typedef long long ll;
5 const int maxn=20005;
6 ll n,ans,cnt[maxn];
7 vector<int> tree[maxn]; //存储边的信息构成一颗树
8
9 void DFS(int now,int pre) //now为当前节点,pre为父亲节点
10 {
11 cnt[now]=1;
12 ll sum=0;
13 int len=tree[now].size(); //以当前节点为根的树的子树的个数
14 for(int i=0;i<len;i++) //遍历所有子树
15 {
16 int x=tree[now][i];
17 if(x==pre) continue; //不包含父亲节点
18 DFS(x,now);
19 cnt[now]+=cnt[x]; //当前节点为根的树的节点总数等于其他所有子树节点的和
20 sum+=cnt[x]*(n-cnt[x]-1); // 子树x与剩余节点数目的乘积
21 }
22 sum+=(cnt[now]-1)*(n-cnt[now]); //父亲节点所在分支也为now的一个子树,也要加上
23 ans=max(ans,sum/2);
24 return;
25 }
26
27 int main()
28 {
29 int t;
30 cin>>t;
31 int kase=1;
32 while(t--)
33 {
34 cin>>n;
35 ans=0;
36 for(int i=0;i<maxn;i++)
37 tree[i].clear(); //清空
38 for(int i=1;i<n;i++)
39 {
40 int a,b;
41 cin>>a>>b;
42 tree[a].push_back(b); //无向图a到b即b到a
43 tree[b].push_back(a);
44 }
45 DFS(1,0);
46 printf("Case #%d: %lld
",kase++,ans);
47 }
48 return 0;
49 }