换了个问法:
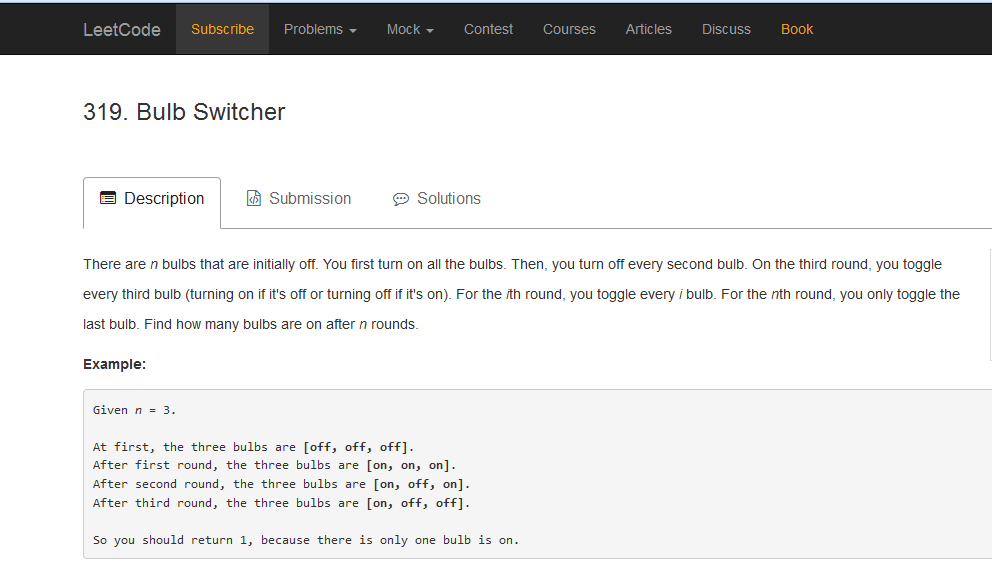
2015盏灯,一开始全部熄灭,序号分别是1-2015,先把1的倍数序号的灯的开关全部按一次,然后把2的倍数的灯的开关全部按一次,然后把3的倍数的开关按一次,以此类推,最后把2015的倍数灯的开关按一次。问最后亮着的灯有多少盏?
A. 43
B. 44
C. 45
D. 46
先来分析一下,因为一开始的时候 2015 盏灯都是熄灭的,按一次灯就开了, 按两次灯就熄灭了,由此可以知道只有按过奇数次的灯才可能是亮着的,题目中还有一个信息,就是把 1 的倍数的灯按一次,把 2 倍数的灯按一次,把 3 倍数的灯按一次,如此类推,这不就是求每个数的公约数吗?因此结合第一第二个条件,我们就可以把题目演化成求1-2015中有哪些数的公约数是奇数个的。如:1 , 4, 9 , 16..... (注:一个数的约数必然包括1及其本身) 这样算还是比较麻烦,我们可以继续把题目演化,求哪些数的公约数是奇数个其实也就是求哪些数是平方数,为什么呢?因为约数都是成对出现的,平方数是由两个相同的约数得到的,但是算个数是只算一个。偶数加奇数是奇数。所以只有平方数才有奇数个约数。最后,问题就变得很简单了,其实就是求1-2015中有多少个平方数,换个角度就是:44^2<2015<45^2,最后的答案就是 44 个,选 B