题链:
http://www.lydsy.com/JudgeOnline/problem.php?id=3144
题解:
"这是一个经典的最小割模型" ---引用自别人的博客
。。。。。。。。。。。。。
苦酒入喉心作痛,我怎么就是建不出图呢?
先考虑部分限制:
1).每个纵轴上只选择一个点。
这个建图比较简单,如下,(把点权放在它上方的边上):
(x,y,z) –> (x,y,z+1) : (w[x][y][z])
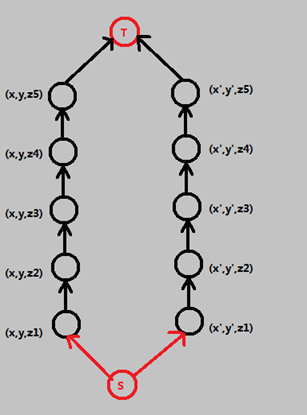
只用求一个最小割即可。
另外,再添加另一个限制:
2).相邻的纵轴上选择的点的竖直距离不超过D(假设 D=1)
(x,y,z) –> (x',y',z-D ) : (INF) (x,y)与(x',y'相邻)
这个就只有 kou nao dai 了。。。
因为在上图中每条路上只割一条边。
那么假设在左边的路上割了 E1。
那么显然,只能在右边的路上割黄色区域。
如果建一条绿边(竖直向下D个单位)的话,显然右边黄色区域下面的边就割不了了。
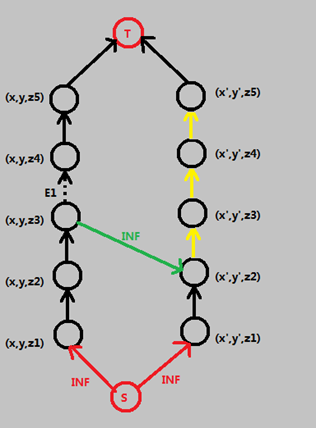
那么又是如何限制黄色区域的上界的呢。
考虑如果选择割了右边黄色区域上面的某一条边 E2,
那类似绿边那样的建一条蓝色的边,
显然这无法形成一个割,因为存在可继续增广的路。
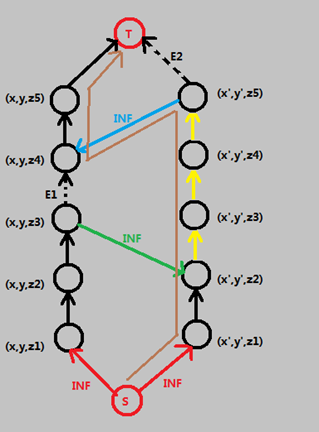
所以为了形成最下割,在右边的选择区域就固定在了黄色区域里。
代码:
#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
#define MAXN 100050
#define MAXM 1000050
#define INF 0x3f3f3f3f
using namespace std;
const int mv[4][2]={{0,1},{0,-1},{1,0},{-1,0}};
struct Edge{
int to[MAXM],cap[MAXM],nxt[MAXM],head[MAXN],ent;
void Init(){ent=2;}
void Adde(int u,int v,int w){
to[ent]=v; cap[ent]=w; nxt[ent]=head[u]; head[u]=ent++;
to[ent]=u; cap[ent]=0; nxt[ent]=head[v]; head[v]=ent++;
}
int Next(int i,bool type){
return type?head[i]:nxt[i];
}
}E;
int d[MAXN],cur[MAXN];
int P,Q,R,D,S,T;
int idx(int x,int y,int z){
return P*Q*(z-1)+(x-1)*Q+y;
}
bool bfs(){
queue<int>q; int u,v;
memset(d,0,sizeof(d));
q.push(S); d[S]=1;
while(!q.empty()){
u=q.front(); q.pop();
for(int i=E.Next(u,1);i;i=E.Next(i,0)){
v=E.to[i];
if(d[v]||!E.cap[i]) continue;
d[v]=d[u]+1; q.push(v);
}
}
return d[T];
}
int dfs(int u,int reflow){
if(u==T||!reflow) return reflow;
int flowout=0,f,v;
for(int &i=cur[u];i;i=E.Next(i,0)){
v=E.to[i];
if(d[v]!=d[u]+1) continue;
f=dfs(v,min(reflow,E.cap[i]));
flowout+=f; E.cap[i^1]+=f;
reflow-=f; E.cap[i]-=f;
if(!reflow) break;
}
if(!flowout) d[u]=0;
return flowout;
}
int Dinic(){
int flow=0;
while(bfs()){
memcpy(cur,E.head,sizeof(E.head));
flow+=dfs(S,INF);
}
return flow;
}
int main()
{
E.Init();
scanf("%d%d%d%d",&P,&Q,&R,&D);
S=P*Q*R+1; T=P*Q*R+2;
for(int k=1,x,_i,_j,to;k<=R;k++)
for(int i=1;i<=P;i++)
for(int j=1;j<=Q;j++){
scanf("%d",&x);
if(k==R) to=T; else to=idx(i,j,k+1);
E.Adde(idx(i,j,k),to,x);
if(k-D<=0) continue;
for(int l=0;l<4;l++){
_i=i+mv[l][0];
_j=j+mv[l][1];
if(_i<1||P<_i||_j<1||Q<_j) continue;
E.Adde(idx(i,j,k),idx(_i,_j,k-D),INF);
}
}
for(int i=1;i<=P;i++)
for(int j=1;j<=Q;j++)
E.Adde(S,idx(i,j,1),INF);
int ans=Dinic();
printf("%d",ans);
return 0;
}