●赘述题目
给出一张弦图,求其最小染色数。
●题解
网上的唯一“文献”:《弦图与区间图》(cdq),可以学习学习。(有的看不懂)
摘录几个解决改题所需的知识点:
●子图和诱导子图(一定要弄清楚)
子图:对于一个图G=(V,E) ,满足V'⊆V且E'⊆E的G’=(V',E')称为图G的子图
诱导子图:对于一个图G=(V,E),满足V'⊆V且E'=(所有(u,v)|u⊆V',v⊆V')的G'=(V',E')称为图G诱导子图
●团
若图G=(V,E)的一个子图G'=(V',E')是V'的完全图,则该子图G'称为一个团
●极大团
若一个团G'不是其他任何团的子图,则该团为极大图
●最大团
点数最多的团
●团数:
最大团的点数
●色数:
对图G进行染色,使得任何相邻的两点颜色不同,所需要的最少颜色数
一个性质:对于一个图G,满足团数≤色数
别人家的证明:因为团是完全图,一个n个点的完全图的色数为n,所以对于一个图的团数(极大团的点的个数)等于色数。
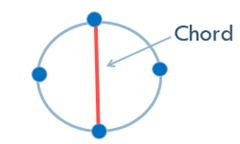
●弦:
连接环中的不相邻的两点的边
●弦图:一个无向图称为弦图当图中任意长度大于3的环都至少有一个弦
(即一个无向图不存在长度大于3的环则称为弦图)
一个性质:弦图的诱导子图也是弦图
另一个性质:弦图中,团数==色数
●单纯点:
对于一个点v,设n(v)表示与v相连的点集,若V'=v∪n(v)形成的诱导子图是一个团,则v是单纯点
●完美消除序列
一个点的序列(图的每个点出现一次):v1,v2,v3,...,vn,满足任意vi在{vi,vi+1,vi+2,...,vn}的诱导子图中是一个单纯点
●判断图G为弦图:ZOJ 1015 Fishing Net
MCS(最大势算法):
●用lab[ ]记录每个点的势(与多少标记的点相邻)
每次取出势最大的点(刚开始都为0),从后往前放入一个序列,并标记这个点为已标记,并更新与改点相连的点的势(+1),重复该操作,直到取完所有点。(用链表做到O(n(点数)+m(边数)))
●那么序列构造出来了,到底是不是完美消除序列呢(即是不是弦图)还需要check一下
check(优化后的,O(n+m)):
对于每个点vi,找出{vi,vi+1,vi+2,...,vn}中与它相连的点,并用vmin记录与它相连的点中在序列中位置最小的那个点,只需判断vmin是否和那些点相连,若没有连边,则不是完美消除序列,即不是弦图。
如果对于每个vi都成立,则是完美消除序列,即是弦图。
ZOJ 1015 代码(MCS判弦图):
#include<cstdio> #include<cstring> #include<iostream> #include<queue> using namespace std; struct edge{ int to,next; }e[2000050]; int head[1005],lab[1005],order[1005],g[1005][1005]; int n,m,ent=1; void add(int u,int v) { e[ent]=(edge){v,head[u]};head[u]=ent++; e[ent]=(edge){u,head[v]};head[v]=ent++; } void msc() { bool vis[1005]; memset(vis,0,sizeof(vis)); queue<int> link[1005]; int best=0,u,v,cnt=n; for(int i=1;i<=n;i++) link[0].push(i),lab[i]=0; while(!link[best].empty()||best) { if(link[best].empty()){best--; continue;} u=link[best].front(); link[best].pop(); if(vis[u]) continue; vis[u]=1; order[u]=cnt--; for(int i=head[u];i;i=e[i].next) { v=e[i].to; if(vis[v]) continue; lab[v]++; if(lab[v]>best) best=lab[v]; link[lab[v]].push(v); } } } bool check() { int p[1005],pnt,mi,ni; for(int i=1;i<=n;i++) { pnt=0;mi=0x3f3f3f3f; for(int j=head[i];j;j=e[j].next) { if(order[e[j].to]<order[i]) continue; if(mi>order[e[j].to]) mi=order[e[j].to],ni=e[j].to; p[++pnt]=e[j].to; } for(int j=1;j<=pnt;j++) { if(p[j]==ni) continue; if(!g[ni][p[j]]) return 0; } } return 1; } void init() { memset(g,0,sizeof(g)); memset(head,0,sizeof(head)); ent=1; } int main() { while(scanf("%d%d",&n,&m)&&(n+m)) { init(); for(int i=1,a,b;i<=m;i++) scanf("%d%d",&a,&b),g[a][b]=g[b][a]=1,add(a,b); msc(); if(check()) printf("Perfect "); else printf("Imperfect "); } return 0; }
那么对于BZOJ 1006这个题,已经告诉了我们,题目输入一个弦图,于是我们只需要用MCS求出完美消除序列,然后求团数(最大团点数):
因为在完美消除序列中的每个点vi,它在{vi,vi+1,vi+2,...,vn}形成的诱导子图中是单纯点,即我们找出在{vi,vi+1,vi+2,...,vn}中与vi相连的点,形成的点集V'=(那些点∪vi) 的诱导子图则是一个团,可以得出该团的点数,由此可以通过枚举vi找出团数(最大团点数)
BZOJ 1006 代码(n+m)
#include<queue> #include<cstdio> #include<cstring> #include<iostream> using namespace std; struct edge{ int to,next; }e[2000005]; int head[10005],rank[10005],sa[10005]; int n,m,ent=1,ans; void add(int u,int v) { e[ent]=(edge){v,head[u]};head[u]=ent++; e[ent]=(edge){u,head[v]};head[v]=ent++; } void msc() { bool vis[10005]; int lab[10005]; memset(vis,0,sizeof(vis)); queue<int> link[10005]; int best=0,u,v,cnt=n; for(int i=1;i<=n;i++) link[0].push(i),lab[i]=0; while(!link[best].empty()||best) { if(link[best].empty()){best--; continue;} u=link[best].front(); link[best].pop(); if(vis[u]) continue; vis[u]=1; rank[u]=cnt; sa[cnt]=u; cnt--; for(int i=head[u];i;i=e[i].next) { v=e[i].to; if(vis[v]) continue; lab[v]++; if(lab[v]>best) best=lab[v]; link[lab[v]].push(v); } } } int main() { scanf("%d%d",&n,&m); for(int i=1,a,b;i<=m;i++) scanf("%d%d",&a,&b),add(a,b); msc(); for(int i=n,u,v,cnt;i>=1;i--) { u=sa[i]; cnt=1; for(int j=head[u];j;j=e[j].next) { v=e[j].to; if(rank[v]<i) continue; cnt++; } ans=max(ans,cnt); } printf("%d",ans); return 0; }
时间复杂度分析:以上面程序的main( )里的求团数为例:
看似有两层循环,但我们来这么考虑:
第一层枚举了n个点;
两层循环全部结束后,每条边都被枚举了两次(2m)
所以总的复杂度为O(n+m)
●注:自学了一点皮毛,如果文中有问题,欢迎指出,谢谢。