第2章 信息的表示和处理
2.1 信息的存储
1. 大多数计算机使用8位的块,或者字节,作为最小的可寻址的存储器单位,而不是在存储器中访问单独的位。
机器级程序将存储器视为一个非常大的字节数组,称为虚拟存储器。
存储器的每个字节都由一个唯一的数字来标识,称为它的地址,所有可能地址的集合称为虚拟地址空间。
2. C语言中一个指针的值(无论它是指向一个整数、一个结构或是某个其他程序对象)都是某个存储块的第一个字节的虚拟地址。C编译器还把每个指针和类型信息联系起来,这样就可以根据指针值的类型,生成不同的机器级代码来访问存储在指针所指向位置处的值。
3. 对于一个字长为w位的机器而言,虚拟地址的范围为0~2w-1,程序最多访问2w个字节。
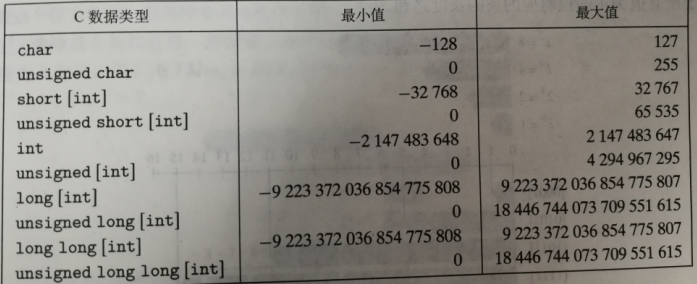
32位机器上C语言的整型数据类型的典型取值范围:
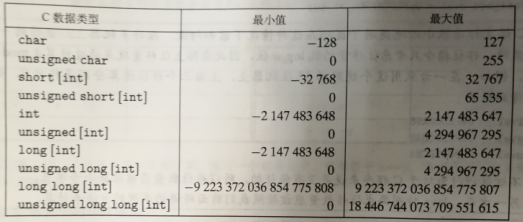
64位机器上C语言的整型数据类型的典型取值范围:
4. 小端存储法:按照从最低有效字节到最高有效字节的顺序存储对象;
大端存储法:按照从最高有效字节到最低有效字节的顺序存储对象。
5. 在使用ASCII码作为字符码的任何系统上都将得到相同的结果,与字节顺序和字大小规则无关。因而,文本数据比二进制数据具有更强的平台独立性。
6. 逻辑运算符&&和||与它们的对应的位级运算&和|之间一个重要的区别是:如果对第一个参数求值就能确定表达式的结果,那么逻辑运算符就不会对第二个参数求值。
7. x向左移动k位,则丢弃最高的k位,并在右端补k个0。
逻辑右移在左端补k个0;算数右移是在左端补k个最高有效位的值。
对于无符号数据(也就是以限定词unsigned声明的整型对象),右移必须是逻辑的;几乎所有的编译器都对有符号数据使用算数右移。
2.2 整数表示
1. 就w位的补码所表示值的范围而言:能表示的最小值是位向量[10......0],其整数值为TMinw=-2w-1;而最大值是位向量[01......1],其整数值为TMaxw=2w-1-1。
2. 对大多数C语言的实现而言,处理同样字长的有符号数和无符号数之间相互转换的一般规律则是:保持位值不变,只是改变解释这些位的方法。
尽管C语言标准没有指定有符号数要采用某种表示,但是几乎所有的机器都使用补码。通常,大多数数字都默认是有符号的。
C语言中,当用printf输出数值时,分别用指示符%d、%u和%x以有符号十进制、无符号十进制和十六进制格式输出一个数字。
C语言运算时,如果它的一个运算数是有符号的而另一个运算数是无符号的,那么C语言会隐式地将有符号参数强制类型转换为无符号数,并假设这两个数都是非负的,来执行这个运算。
C语言标准中,当把short转换成unsigned时,首先要改变其大小,之后再完成从有符号到无符号的转换。
3. 将一个无符号数转换为一个更大的数据类型,只需要简单地在表示的开头添加0,这种运算称为零扩展;
将一个补码数字转换为一个更大的数据类型,则在表示中添加最高有效位的值的副本,这种运算称为符号扩展。
4. 截断是指将一个k位数字x=[xw-1,xw-2,......,x0] ,丢弃高w-k位,得到一个位向量x'=[xk-1,xk-2,......,x0]。
2.3 整数运算
1. 算术溢出,是指完整的整数结果不能放到数据类型的字长限制中去。
2. 无符号加法:若无符号x、y做运算s=x+y,则溢出的判断方法为:s<x(或者等价为s<y)。
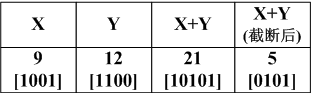
3. 补码加法:

注:情况1指计算结果发生负溢出;情况2,3指计算结果正常;情况4指计算结果发生正溢出
4. 补码的非:对于范围在-2w-1≤X<2w-1,若X≠-2w-1,则它的加法逆元就是-X;若X=-2w-1,则加法逆元是它本身。
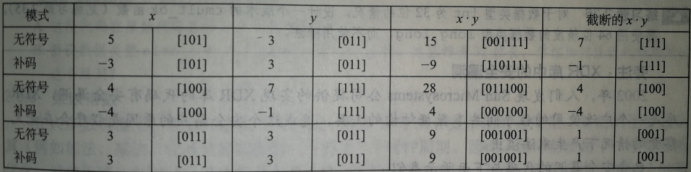
5. 无符号乘法以及补码乘法:
6. 乘以常数:由于整数乘法比移位和加法的代价要大得多,许多C语言编译器试图以移位、加法和减法的组合来消除很多整数乘以常数的情况。
如:x*14。利用等式14=23+22+21,编译器会将乘法重写为(x<<3)+(x<<2)+(x<<1);
也可以利用等式14=24-21,编译器会将乘法写为(x<<4)-(x<<1)。
7. 除以2的幂:无符号数和补码数分别使用逻辑右移和算术右移来完成该计算。
无符号数除以2的幂:

有符号数除以2的幂:

从上面两个表格中可以看出:对于无符号数的右移除2的幂,移位总是舍入到零,与整数除法的规则一样;而对于补码数,在进行右移除2幂时,移位导致结果向下舍入,不是像规则需要的那样向零舍入,需要在移位之前引入“偏置”值,即有[x/y]=[(x+y-1)/y]。
加入“偏置”后,补码数除以2幂的计算结果:

综之,对于除以2的幂运算,进行算数右移的补码机器C表达式为:(x<0? (x+(1<<k)-1):x) >> k,其中y=2k。
2.4 浮点数
1. 舍入
向偶数舍入:<1> 试图找到一个最接近的匹配值
<2> 在确定两个可能结果中间数值的舍入效果时,将数字向上或向下舍入,使得结果的最低有效数字是偶数。
向零舍入:把正数向下舍入,把负数向上舍入。
向下舍入:把正数和负数都向下舍入。
向上舍入:把正数和负数都向上舍入。

2. 浮点运算:由于在运算的过程中可能发生溢出,或者由于舍入而失去精度,所以浮点的加法运算和乘法运算都不满足结合性,同时也不满足乘法在加法上的分配性。