题目:返回一个二维整数数组中最大子数组的和。要求: 输入一个二维整形数组,数组里有正数也有负数。 二维数组中连续的一个子矩阵组成一个子数组,每个子数组都有一个和。 求所有子数组的和的最大值。要求时间复杂度为O(n)。结对编程要求: 两人结对完成编程任务。 一人主要负责程序分析,代码编程。 一人负责代码复审和代码测试计划。 讲述两人合作中的过程、体会以及如何解决冲突。编写思路: 题目的重点在于如何去求子数组和的最大值,通过网上查找资料,得到方法:将二维整型数组求最大子数组之和化为求一位最大子数组之和,将二维整型数组求最大子数组之和化为求一位最大子数组之和。主要代码: #include<iostream> using namespace std; void main ()
{
int x,y,i,j,m=0,A[100][100];
cout<<"输入矩阵的行()和列";
cin>>x>>y;
if(x>100||y>100)
{
cout<<"请重新输入:";
cin>>x>>y;
}
for(i=0;i<x;i++)
{
for(j=0;j<y;j++)
{
cin>>A[i][j];
}
}
int sum[100]={0},max=0,result=A[0][0];
for(i=0;i<x;i++)//确定子数组的最大上界(为第i行)
{
while(m+i<x)//确定子数组有m+i行
{
for(j=0;j<y;j++)
{
sum[j]=sum[j]+A[m+i][j];
}
max=0;
for(j=0;j<y;j++)
{
if(max+sum[j]>max)
{
max=max+sum[j];
}
else
{
max=sum[j];
}
if(max>result)
{
result=max;
}
}
m++;
}
m=0;
for(j=0;j<y;j++)
{ sum[j]=0;
}
}
cout<<result;
}运行截图: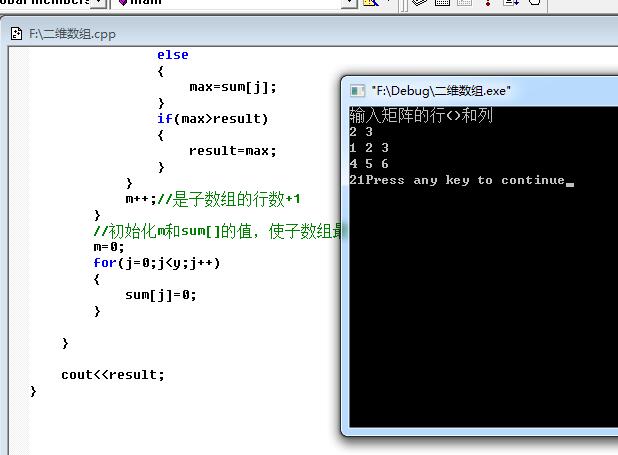
{
int x,y,i,j,m=0,A[100][100];
cout<<"输入矩阵的行()和列";
cin>>x>>y;
if(x>100||y>100)
{
cout<<"请重新输入:";
cin>>x>>y;
}
for(i=0;i<x;i++)
{
for(j=0;j<y;j++)
{
cin>>A[i][j];
}
}
int sum[100]={0},max=0,result=A[0][0];
for(i=0;i<x;i++)//确定子数组的最大上界(为第i行)
{
while(m+i<x)//确定子数组有m+i行
{
for(j=0;j<y;j++)
{
sum[j]=sum[j]+A[m+i][j];
}
max=0;
for(j=0;j<y;j++)
{
if(max+sum[j]>max)
{
max=max+sum[j];
}
else
{
max=sum[j];
}
if(max>result)
{
result=max;
}
}
m++;
}
m=0;
for(j=0;j<y;j++)
{ sum[j]=0;
}
}
cout<<result;
}运行截图:


: 仔细学习了数组相关知识,思考如何进行最大子数组的判断,参考园友的处理方式与队友理解最后有了这个方法。通过这次练习,发现自己编程能力仍然很欠缺,缺少编程实践只能通过去查阅资料来获得思路,这次练习自己的完成度也不是很高,有待加强。发生冲突时,先通过互相交流意见争取达成统一意见,再从网上查资料编程实践,选择对的的方法.