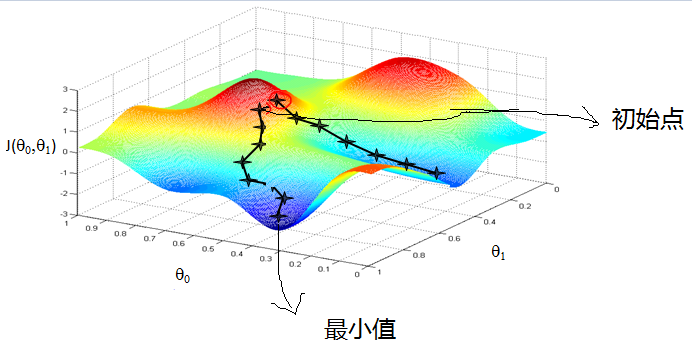
- 梯度下降法(Gradient descent)是一个一阶最优化算法,通常也称为最速下降法。 要使用梯度下降法找到一个函数的局部极小值,必须向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离点进行迭代搜索。如果相反地向梯度正方向迭代进行搜索,则会接近函数的局部极大值点;这个过程则被称为梯度上升法。
- 本文将从最优化问题谈起,回顾导数与梯度的概念,引出梯度下降的数据推导;概括三种梯度下降方法的优缺点,并用Python实现梯度下降(附源码)。
1 最优化问题
- 最优化问题是求解函数极值的问题,包括极大值和极小值。
- 微积分为我们求函数的极值提供了一个统一的思路:找函数的导数等于0的点,因为在极值点处,导数必定为0。这样,只要函数的可导的,我们就可以用这个万能的方法解决问题,幸运的是,在实际应用中我们遇到的函数基本上都是可导的。
- 机器学习之类的实际应用中,我们一般将最优化问题统一表述为求解函数的极小值问题,即:
- 其中(x)称为优化变量,(f)称为目标函数。极大值问题可以转换成极小值问题来求解,只需要将目标函数加上负号即可:
2 导数与梯度
- 梯度是多元函数对各个自变量偏导数形成的向量。多元函数的梯度表示:
-
如果Hessian矩阵正定,函数有极小值;如果Hessian矩阵负定,函数有极大值;如果Hessian矩阵不定,则需要进一步讨论。
-
如果二阶导数大于0,函数有极小值;如果二阶导数小于0,函数有极大值;如果二阶导数等于0,情况不定。
问题:为何不直接求导,令导数等于零去求解?
- 直接求函数的导数,有的函数的导数方程组很难求解,比如下面的方程:
3 梯度下降的推导过程
- 回顾一下泰勒展开式
- 多元函数(f(x))在x处的泰勒展开:
3.1 数学推导
目标是求多元函数(f(x))的极小值。梯度下降法是通过不断迭代得到函数极小值,即如能保证(f(x +Delta x))比(f(x))小,则不断迭代,最终能得到极小值。想象你在山顶往山脚走,如果每一步到的位置比之前的位置低,就能走到山脚。问题是像哪个方向走,能最快到山脚呢?
由泰勒展开式得:
如果(Delta x)足够小,可以忽略(o(Delta x)),则有:
于是只有:
能使
因为( abla f(x))与(Delta x)均为向量,于是有:
其中,( heta)是向量( abla f(x))与(Delta x)的夹角,(| abla f(x)|)与(|Delta x|)是向量对应的模。可见只有当
才能使得
又因
可见,只有当
即( heta = pi)时,函数数值降低最快。此时梯度和(Delta x)反向,即夹角为180度。因此当向量(Delta x)的模大小一定时,取
即在梯度相反的方向函数值下降的最快。此时函数的下降值为:
只要梯度不为(0),往梯度的反方向走函数值一定是下降的。直接用可能会有问题,因为(x+Delta x)可能会超出(x)的邻域范围之外,此时是不能忽略泰勒展开中的二次及以上的项的,因此步伐不能太大。
一般设:
其中(alpha)为一个接近于(0)的正数,称为步长,由人工设定,用于保证(x+Delta x)在x的邻域内,从而可以忽略泰勒展开中二次及更高的项,则有:
此时,(x)的迭代公式是:
只要没有到达梯度为(0)的点,则函数值会沿着序列(x_{k})递减,最终会收敛到梯度为(0)的点,这就是梯度下降法。
迭代终止的条件是函数的梯度值为(0)(实际实现时是接近于(0)),此时认为已经达到极值点。注意我们找到的是梯度为(0)的点,这不一定就是极值点,后面会说明。
4 实现的细节
-
初始值的设定
一般的,对于不带约束条件的优化问题,我们可以将初始值设置为0,或者设置为随机数,对于神经网络的训练,一般设置为随机数,这对算法的收敛至关重要。 -
学习率的设定
学习率设置为多少,也是实现时需要考虑的问题。最简单的,我们可以将学习率设置为一个很小的正数,如0.001。另外,可以采用更复杂的策略,在迭代的过程中动态的调整学习率的值。比如前1万次迭代为0.001,接下来1万次迭代时设置为0.0001。
5 存在的问题
- 局部极小值
- 梯度下降可能在局部最小的点收敛。
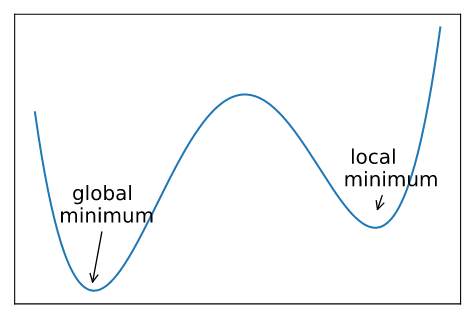
- 梯度下降可能在局部最小的点收敛。
- 鞍点
- 鞍点是指梯度为0,Hessian矩阵既不是正定也不是负定,即不定的点。如函数(x^2-y^2)在((0,0))点梯度为0,但显然不是局部最小的点,也不是全局最小的点。
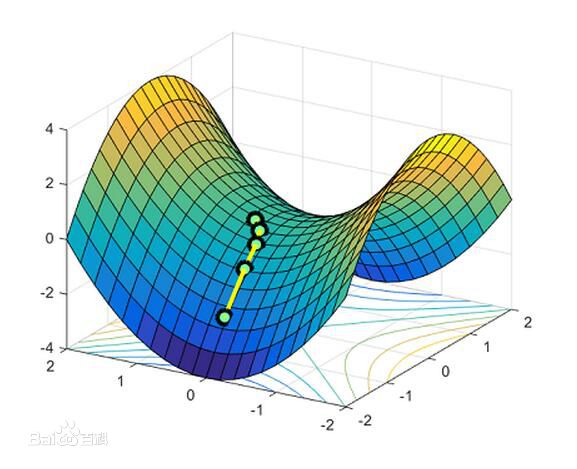
- 鞍点是指梯度为0,Hessian矩阵既不是正定也不是负定,即不定的点。如函数(x^2-y^2)在((0,0))点梯度为0,但显然不是局部最小的点,也不是全局最小的点。
6 三种梯度下降的实现
- 批量梯度下降法:Batch Gradient Descent,简称BGD。求解梯度的过程中用了全量数据。
- 全局最优解;易于并行实现。
- 计算代价大,数据量大时,训练过程慢。
- 随机梯度下降法:Stochastic Gradient Descent,简称SGD。依次选择单个样本计算梯度。
- 优点:训练速度快;
- 缺点:准确度下降,并不是全局最优;不易于并行实现。
- 小批量梯度下降法:Mini-batch Gradient Descent,简称MBGD。每次更新参数时使用b个样本。(b一般为10)。
- 两种方法的性能之间取得一个折中。
7 用梯度下降法求解多项式极值
7.1 题目
(argminfrac{1}{2}[(x_{1}+x_{2}-4)^2 + (2x_{1}+3x_{2}-7)^2 + (4x_{1}+x_{2}-9)^2])
7.2 python解题
以下只是为了演示计算过程,便于理解梯度下降,代码仅供参考。更好的代码我将在以后的文章中给出。
# 原函数
def argminf(x1, x2):
r = ((x1+x2-4)**2 + (2*x1+3*x2 - 7)**2 + (4*x1+x2-9)**2)*0.5
return r
# 全量计算一阶偏导的值
def deriv_x(x1, x2):
r1 = (x1+x2-4) + (2*x1+3*x2-7)*2 + (4*x1+x2-9)*4
r2 = (x1+x2-4) + (2*x1+3*x2-7)*3 + (4*x1+x2-9)
return r1, r2
# 梯度下降算法
def gradient_decs(n):
alpha = 0.01 # 学习率
x1, x2 = 0, 0 # 初始值
y1 = argminf(x1, x2)
for i in range(n):
deriv1, deriv2 = deriv_x(x1, x2)
x1 = x1 - alpha * deriv1
x2 = x2 - alpha * deriv2
y2 = argminf(x1, x2)
if y1 - y2 < 1e-6:
return x1, x2, y2
if y2 < y1:
y1 = y2
return x1, x2, y2
# 迭代1000次结果
gradient_decs(1000)
# (1.9987027392533656, 1.092923742270406, 0.4545566995437954)
参考文献
- 《机器学习与应用》
- https://zh.wikipedia.org/wiki/梯度下降法