二叉树

目录

• 二叉树
  • 遍历路径
  • 树遍历框架
  • 例子1(二叉搜索树转换为单向链表)
  • 例子2(删除二叉搜索树中的 key 对应的节点)
  • 例子3(根据前序中序遍历结果重建二叉树)

二叉树

二叉树是一种非常重要的数据结构，非常多其他数据结构都是基于二叉树的基础演变而来的。对于二叉树，有深度遍历和广度遍历，深度遍历有前序、中序以及后序三种遍历方法，广度遍历即我们寻常所说的层次遍历。由于树的定义本身就是递归定义，因此採用递归的方法去实现树的三种遍历不仅easy理解并且代码非常简洁，而对于广度遍历来说，须要其他数据结构的支撑。比方堆了。所以。对于一段代码来说，可读性有时候要比代码本身的效率要重要的多。

遍历路径

前序遍历：根->左->右

中序遍历：左->根->右（最重要）

后续遍历：左->右->根

层次遍历：根->左->右

树遍历框架

所有树的遍历均可以套用树遍历框架

void traverse(TreeNode root) {
    // 前序遍历
    traverse(root.left)
    // 中序遍历
    traverse(root.right)
    // 后序遍历
}

例子1(二叉搜索树转换为单向链表)

二叉树数据结构TreeNode可用来表示单向链表（其中left置空，right为下一个链表节点）。实现一个方法，把二叉搜索树转换为单向链表，要求值的顺序保持不变，转换操作应是原址的，也就是在原始的二叉搜索树上直接修改。

返回转换后的单向链表的头节点。

示例：

输入： [4,2,5,1,3,null,6,0]
输出： [0,null,1,null,2,null,3,null,4,null,5,null,6]

    //上级节点
	TreeNode preNode;
    //头节点
    TreeNode headNode;
    public TreeNode convertBiNode(TreeNode root) {
        if (root == null) {
            return null;
        }
        search(root);
        return headNode;
    }

    /**
     * 中序遍历框架
     * search(node.left)
     * do current value
     * search(node.right)
     * @param node
     */
    public void search(TreeNode node) {
        if (node == null) {
            return;
        }
        //1.遍历左节点
        search(node.left);

        //2.处理当前节点
        if (preNode != null) {
            //当前节点设置为上个节点的右节点
            preNode.right = node;
        } else {
            headNode = node;
        }
        //当前节点的左节点设置为null
        node.left = null;
        preNode = node;
        //3.遍历右节点
        search(node.right);
    }

例子2(删除二叉搜索树中的 key 对应的节点)

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点；
如果找到了，删除它。
说明： 要求算法时间复杂度为 O(h)，h 为树的高度。

分析：

1. 当前节点没有左子节点

   返回root.right

2. 当前节点没有右子节点

   返回root.left

3. 当前节点既有左子节点和右子节点时

   1. 找到右子节点下面最后一个左子结点

   2. 将root的左子节点放到右子节点下面最后一个左子结点的左子节点上

   3. 直接返回右子节点

BTS数遍历框架

二叉搜索树（Binary Search Tree，简称 BST）是一种很常用的的二叉树。它的定义是：

一个二叉树中，任意节点的值要大于等于左子树所有节点的值，且要小于等于右边子树的所有节点的值

void BST(TreeNode root, int target) {
    if (root.val == target)
        // 找到目标，做点什么
    if (root.val < target) 
        //目标比节点值大，目标肯定在右节点
        BST(root.right, target);
    if (root.val > target)
        //目标比节点值小，目标肯定在左节点
        BST(root.left, target);
}

public TreeNode deleteNode(TreeNode root, int key) {
    if(root == null) {
        return null;
    }
    if(root.val == key){
        if(root.right == null){
            return root.left;
        }
        if(root.left == null) {
            return root.right;
        }
        //当目标节点左右子节点都存在时
        TreeNode node = root.right;
        //找到右子节点下面最后一个左子结点
        while(node.left != null){
            node = node.left;
        }
        //将root的左子节点放到右子节点下面最后一个左子结点的左子节点上
        node.left = root.left;
        //直接返回右子节点
        return root.right;
    }else if(key < root.val){
        root.left = deleteNode(root.left,key);
    }else{
        root.right = deleteNode(root.right,key);
    }
    return root;
}

例子3(根据前序中序遍历结果重建二叉树)

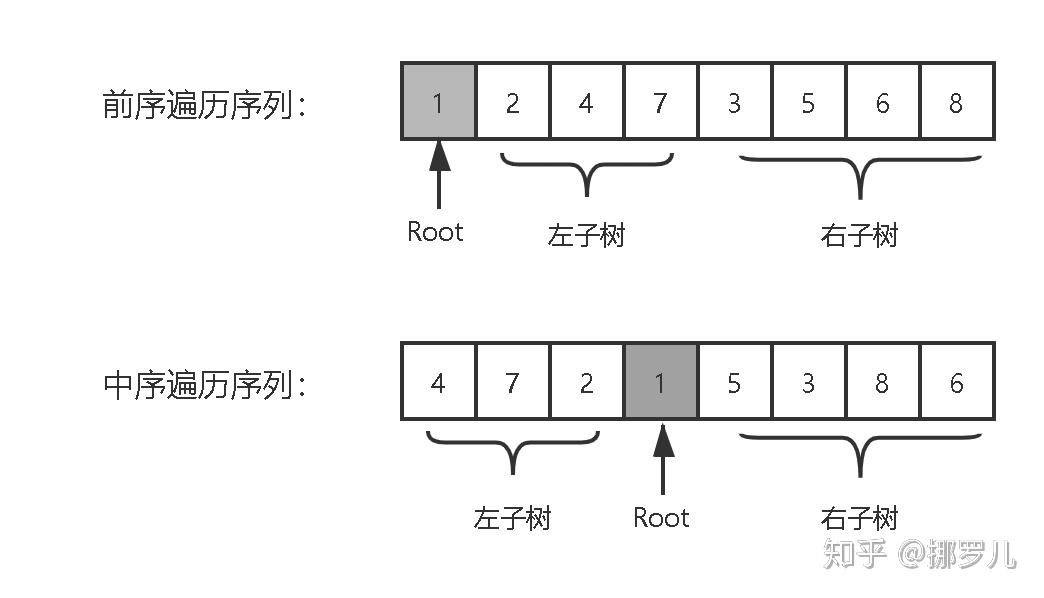
//根据前序中序遍历结果重建二叉树框架
//pre 前序
//mid 中序
TreeNode buildNode(List<Integer> pre,List<Integer> mid){
    if(pre.size() == 0){
        return null;
    }
    //前序第一个值肯定是根节点
    TreeNode root = new TreeNode(pre.get(0));
    //中序对应值的索引作为左右子树分割点
    int i = mid.indexOf(pre.get(0));
    //重建左树
    root.left = buildNode(pre.subList(1,i+1),mid.subList(0,i));
    //重建右树
    root.right = buildNode(pre.subList(i+1,pre.size()),mid.subList(i+1,mid.size()));
    return root;
}

java代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
   
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        List<Integer> mid=new ArrayList<>();
        List<Integer> pre=new ArrayList<>();
        for(int i=0;i<preorder.length;i++){
           pre.add(preorder[i]);
           mid.add(inorder[i]);
        }
        return buildNode(pre,mid);
    }
    /**
    *pre 前序
    *mid 中序
    */
    TreeNode buildNode(List<Integer> pre,List<Integer> mid){
        if(pre.size() == 0){
            //1.递归停止条件
            return null;
        }
        //2.前序第一个是root节点
        TreeNode root = new TreeNode(pre.get(0));
        //3.找到中序中root节点的索引
        //中序遍历的顺序是左->根->右，所以root节点的索引左边一定是左子节点，右边一定是右子节点，
        //这样就就分成左右两部分了
        int i = mid.indexOf(pre.get(0));

        //这样就处理完毕了，接下来就递归重复上面步骤了
        //递归处理左节点数据，前序1->i+1,中序：0->i
        root.left = buildNode(pre.subList(1,i+1),mid.subList(0,i));
        //递归处理右节点数据,前序i+1->end,中序：i+1->end
        root.right = buildNode(pre.subList(i+1,pre.size()),mid.subList(i+1,mid.size()));
        return root;
    }