RC4加密算法是一种对称加密算法。
对称加密算法
对称加密(也叫私钥加密)指加密和解密使用相同密钥的加密算法。有时又叫传统密码算法,就是加密密钥能够从解密密钥中推算出来,同时解密密钥也可以从加密密钥中推算出来。而在大多数的对称算法中,加密密钥和解密密钥是相同的,所以也称这种加密算法为秘密密钥算法或单密钥算法。它要求发送方和接收方在安全通信之前,商定一个密钥。对称算法的安全性依赖于密钥,泄漏密钥就意味着任何人都可以对他们发送或接收的消息解密,所以密钥的保密性对通信的安全性至关重要。
RC4加密算法
RC4算法的特点是算法简单,运行速度快,而且密钥长度是可变的,可变范围为1-256字节(8-2048比特),在如今技术支持的前提下,当密钥长度为128比特时,用暴力法搜索密钥已经不太可行,所以可以预见RC4的密钥范围任然可以在今后相当长的时间里抵御暴力搜索密钥的攻击。实际上,如今也没有找到对于128bit密钥长度的RC4加密算法的有效攻击方法。
RC4算法的原理很简单,包括初始化算法(KSA)和伪随机子密码生成算法(PRGA)两大部分。假设S-box的长度为256,密钥长度为Len。先来看看算法的初始化部分(用C代码表示):
其中,参数1是一个256长度的char型数组,定义为: unsigned char sBox[256];
参数2是密钥,其内容可以随便定义:char key[256];
参数3是密钥的长度,Len = strlen(key);
/*初始化函数*/ void rc4_init(unsigned char*s,unsigned char*key, unsigned long Len) { int i=0,j=0; char k[256]={0}; unsigned char tmp=0; for(i=0;i<256;i++) { s[i]=i; k[i]=key[i%Len]; } for(i=0;i<256;i++) { j=(j+s[i]+k[i])%256; tmp=s[i]; s[i]=s[j];//交换s[i]和s[j] s[j]=tmp; } }
在初始化的过程中,密钥的主要功能是将S-box搅乱,i确保S-box的每个元素都得到处理,j保证S-box的搅乱是随机的。而不同的S-box在经过伪随机子密码生成算法的处理后可以得到不同的子密钥序列,将S-box和明文进行xor运算,得到密文,解密过程也完全相同。
再来看看算法的加密部分(用C代码表示):
其中,参数1是上边rc4_init函数中,被搅乱的S-box;
参数2是需要加密的数据data;
参数3是data的长度.
/*加解密*/ void rc4_crypt(unsigned char*s,unsigned char*Data,unsigned long Len) { int i=0,j=0,t=0; unsigned long k=0; unsigned char tmp; for(k=0;k<Len;k++) { i=(i+1)%256; j=(j+s[i])%256; tmp=s[i]; s[i]=s[j];//交换s[x]和s[y] s[j]=tmp; t=(s[i]+s[j])%256; Data[k]^=s[t]; } }
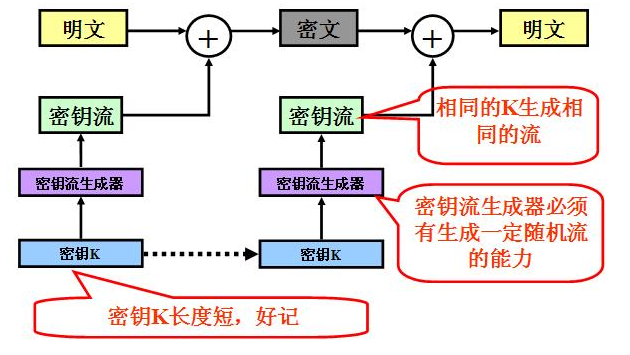
让我们看一看完整程序
//程序开始 #include<stdio.h> #include<string.h> typedef unsigned longULONG; /*初始化函数*/ void rc4_init(unsigned char*s, unsigned char*key, unsigned long Len) { int i = 0, j = 0; char k[256] = { 0 }; unsigned char tmp = 0; for (i = 0; i<256; i++) { s[i] = i; k[i] = key[i%Len]; } for (i = 0; i<256; i++) { j = (j + s[i] + k[i]) % 256; tmp = s[i]; s[i] = s[j];//交换s[i]和s[j] s[j] = tmp; } } /*加解密*/ void rc4_crypt(unsigned char*s, unsigned char*Data, unsigned long Len) { int i = 0, j = 0, t = 0; unsigned long k = 0; unsigned char tmp; for (k = 0; k<Len; k++) { i = (i + 1) % 256; j = (j + s[i]) % 256; tmp = s[i]; s[i] = s[j];//交换s[x]和s[y] s[j] = tmp; t = (s[i] + s[j]) % 256; Data[k] ^= s[t]; } } int main() { unsigned char s[256] = { 0 }, s2[256] = { 0 };//S-box char key[256] = { "justfortest" }; char pData[512] = "这是一个用来加密的数据Data"; unsigned long len = strlen(pData); int i; printf("pData=%s\n", pData); printf("key=%s,length=%d\n\n", key, strlen(key)); rc4_init(s, (unsigned char*)key, strlen(key));//已经完成了初始化 printf("完成对S[i]的初始化,如下:\n\n"); for (i = 0; i<256; i++) { printf("%02X", s[i]); if (i && (i + 1) % 16 == 0)putchar('\n'); } printf("\n\n"); for (i = 0; i<256; i++)//用s2[i]暂时保留经过初始化的s[i],很重要的!!! { s2[i] = s[i]; } printf("已经初始化,现在加密:\n\n"); rc4_crypt(s, (unsigned char*)pData, len);//加密 printf("pData=%s\n\n", pData); printf("已经加密,现在解密:\n\n"); //rc4_init(s,(unsignedchar*)key,strlen(key));//初始化密钥 rc4_crypt(s2, (unsigned char*)pData, len);//解密 printf("pData=%s\n\n", pData); return 0; } //程序完