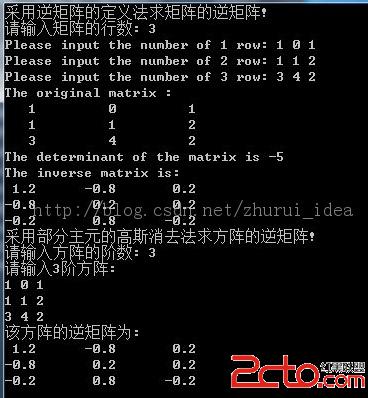
矩阵求逆c++实现

矩阵求逆c++实现

http://www.2cto.com/kf/201405/297388.html

2014-05-02     我来说两句    来源：矩阵求逆c++实现  

收藏    我要投稿

高斯消元法可以用来找出一个可逆矩阵的逆矩阵。设A 为一个N * N的矩阵，其逆矩阵可被两个分块矩阵表示出来。将一个N * N单位矩阵 放在A 的右手边，形成一个N * 2N的分块矩阵B = [A,I] 。经过高斯消元法的计算程序后，矩阵B 的左手边会变成一个单位矩阵I ，而逆矩阵A ^(-1) 会出现在B 的右手边。假如高斯消元法不能将A 化为三角形的格式，那就代表A 是一个不可逆的矩阵。应用上，高斯消元法极少被用来求出逆矩阵。高斯消元法通常只为线性方程组求解。

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263

//******************************** //*** 求任何一个实矩阵的逆*** //******************************** #include "stdafx.h" #include <math.h> #include <malloc.h> #include <iostream> #include <iomanip> using namespace std; #define  N  10                //定义方阵的最大阶数为10 //函数的声明部分 float MatDet(float *p, int n);                    //求矩阵的行列式 float Creat_M(float *p, int m, int n, int k);    //求矩阵元素A(m, n)的代数余之式 void print(float *p, int n);                    //输出矩阵n*n bool Gauss(float A[][N], float B[][N], int n);    //采用部分主元的高斯消去法求方阵A的逆矩阵B int main() {     float *buffer, *p;            //定义数组首地址指针变量     int row, num;                //定义矩阵的行数和矩阵元素个数     int i, j;     float determ;                //定义矩阵的行列式     float a[N][N], b[N][N];     int n;     cout << "采用逆矩阵的定义法求矩阵的逆矩阵! ";     cout << "请输入矩阵的行数: ";     cin >> row;     num = 2 * row * row;     buffer = (float *)calloc(num, sizeof(float));        //分配内存单元     p = buffer;     if (NULL != p)     {         for (i = 0; i < row; i++)         {             cout << "Please input the number of " << i+1 << " row: ";             for (j = 0; j < row; j++)             {                 cin >> *p++;             }         }     }     else     {         cout << "Can't distribute memory ";     }     cout << "The original matrix : ";     print(buffer, row);                //打印该矩阵           determ = MatDet(buffer, row);    //求整个矩阵的行列式     p = buffer + row * row;     if (determ != 0)     {         cout << "The determinant of the matrix is " << determ << endl;         for (i = 0; i < row; i++)    //求逆矩阵         {             for (j = 0; j < row; j++)             {                 *(p+j*row+i) = Creat_M(buffer, i, j, row)/determ;             }         }         cout << "The inverse matrix is: " << endl;         print(p, row);                //打印该矩阵     }     else     {         cout << "The determinant is 0, and there is no inverse matrix! ";     }     free(buffer);        //释放内存空间     cout << "采用部分主元的高斯消去法求方阵的逆矩阵! ";     cout << "请输入方阵的阶数: ";     cin >> n;     cout << "请输入" << n << "阶方阵: ";     //输入一个n阶方阵     for (i = 0; i < n; i++)     {         for (j = 0; j < n; j++)         {             cin >> a[i][j];         }     }     //运用高斯消去法求该矩阵的逆矩阵并输出     if (Gauss(a, b, n))     {         cout << "该方阵的逆矩阵为: ";         for (i = 0; i < n; i++)         {             cout << setw(4);             for (j = 0; j < n; j++)             {                 cout << b[i][j] << setw(10);             }             cout << endl;         }     }        getchar();     return 0; } //----------------------------------------------- //功能: 求矩阵(n*n)的行列式 //入口参数: 矩阵的首地址，矩阵的行数 //返回值: 矩阵的行列式值 //---------------------------------------------- float MatDet(float *p, int n) {     int r, c, m;     int lop = 0;     float result = 0;     float mid = 1;     if (n != 1)     {         lop = (n == 2) ? 1 : n;            //控制求和循环次数,若为2阶，则循环1次，否则为n次         for (m = 0; m < lop; m++)         {             mid = 1;            //顺序求和, 主对角线元素相乘之和             for (r = 0, c = m; r < n; r++, c++)             {                 mid = mid * (*(p+r*n+c%n));             }             result += mid;         }         for (m = 0; m < lop; m++)         {             mid = 1;            //逆序相减, 减去次对角线元素乘积             for (r = 0, c = n-1-m+n; r < n; r++, c--)             {                 mid = mid * (*(p+r*n+c%n));             }             result -= mid;         }     }     else         result = *p;     return result; } //---------------------------------------------------------------------------- //功能: 求k*k矩阵中元素A(m, n)的代数余之式 //入口参数: k*k矩阵的首地址，矩阵元素A的下标m,n,矩阵行数k //返回值: k*k矩阵中元素A(m, n)的代数余之式 //---------------------------------------------------------------------------- float Creat_M(float *p, int m, int n, int k) {     int len;     int i, j;     float mid_result = 0;     int sign = 1;     float *p_creat, *p_mid;     len = (k-1)*(k-1);            //k阶矩阵的代数余之式为k-1阶矩阵     p_creat = (float*)calloc(len, sizeof(float)); //分配内存单元     p_mid = p_creat;     for (i = 0; i < k; i++)     {         for (j = 0; j < k; j++)         {             if (i != m && j != n) //将除第i行和第j列外的所有元素存储到以p_mid为首地址的内存单元             {                 *p_mid++ = *(p+i*k+j);             }         }     }     sign = (m+n)%2 == 0 ? 1 : -1;    //代数余之式前面的正、负号     mid_result = (float)sign*MatDet(p_creat, k-1);     free(p_creat);     return mid_result; } //----------------------------------------------------- //功能: 打印n*n矩阵 //入口参数: n*n矩阵的首地址,矩阵的行数n //返回值: 无返回值 //----------------------------------------------------- void print(float *p, int n) {     int i, j;     for (i = 0; i < n; i++)     {         cout << setw(4);         for (j = 0; j < n; j++)         {             cout << setiosflags(ios::right) << *p++ << setw(10);         }         cout << endl;     } } //------------------------------------------------------------------ //功能: 采用部分主元的高斯消去法求方阵A的逆矩阵B //入口参数: 输入方阵，输出方阵，方阵阶数 //返回值: true or false //------------------------------------------------------------------- bool Gauss(float A[][N], float B[][N], int n) {     int i, j, k;     float max, temp;     float t[N][N];                //临时矩阵     //将A矩阵存放在临时矩阵t[n][n]中     for (i = 0; i < n; i++)            {         for (j = 0; j < n; j++)         {             t[i][j] = A[i][j];         }     }     //初始化B矩阵为单位阵     for (i = 0; i < n; i++)            {         for (j = 0; j < n; j++)         {             B[i][j] = (i == j) ? (float)1 : 0;         }     }     for (i = 0; i < n; i++)     {         //寻找主元         max = t[i][i];         k = i;         for (j = i+1; j < n; j++)         {             if (fabs(t[j][i]) > fabs(max))             {                 max = t[j][i];                 k = j;             }         }         //如果主元所在行不是第i行，进行行交换         if (k != i)         {             for (j = 0; j < n; j++)             {                 temp = t[i][j];                 t[i][j] = t[k][j];                 t[k][j] = temp;                 //B伴随交换                 temp = B[i][j];                 B[i][j] = B[k][j];                 B[k][j] = temp;             }         }         //判断主元是否为0, 若是, 则矩阵A不是满秩矩阵,不存在逆矩阵         if (t[i][i] == 0)         {             cout << "There is no inverse matrix!";             return false;         }         //消去A的第i列除去i行以外的各行元素         temp = t[i][i];         for (j = 0; j < n; j++)         {             t[i][j] = t[i][j] / temp;        //主对角线上的元素变为1             B[i][j] = B[i][j] / temp;        //伴随计算         }         for (j = 0; j < n; j++)        //第0行->第n行         {             if (j != i)                //不是第i行             {                 temp = t[j][i];                 for (k = 0; k < n; k++)        //第j行元素 - i行元素*j列i行元素                 {                     t[j][k] = t[j][k] - t[i][k]*temp;                     B[j][k] = B[j][k] - B[i][k]*temp;                 }             }         }     }     getchar();     return true; }</iomanip></iostream></malloc.h></math.h>

实验结果：