46. Permutations

Given a collection of distinct numbers, return all possible permutations.

For example,
[1,2,3] have the following permutations:

[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]
来源： https://leetcode.com/problems/permutations/

分析

方法一：

因为每个元素只能使用一次，所以使用一个数组，来记录该元素是否已经在上一级被使用过，如果使用过，则跳过，不进行DFS。该方法使用额外的数组来记录nums[i]是否被使用，同时每次的递归调用都会创建新的result，占用额外空间。

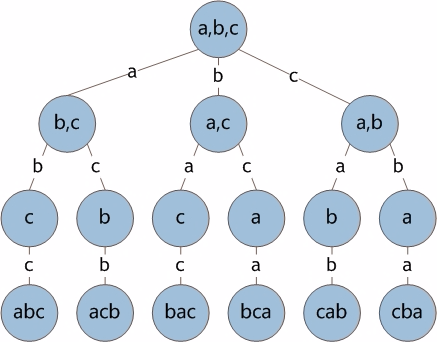
生成的过程类似与下图：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

class Solution { public:     vector<vector<int>> permute(vector<int>& nums) {         vector<bool> t(nums.size(),false);         vector<vector<int>> results;         helper(results, vector<int>{}, t, nums);         return results;     }           void helper(vector<vector<int>> & results, vector<int> result, vector<bool> & t, vector<int> & nums){         for(int i = 0; i < t.size(); ++i){             if(t[i] == true) continue;             result.push_back(nums[i]);             t[i] = true;             if(result.size() == t.size())                 results.push_back(result);             else                 helper(results, result, t, nums);                           result.pop_back();             t[i] = false;         }     } };

方法二：

http://www.cnblogs.com/nokiaguy/archive/2008/05/11/1191914.html

全排列是将一组数按一定顺序进行排列，如果这组数有n个，那么全排列数为n!个。现以{1, 2, 3, 4, 5}为

例说明如何编写全排列的递归算法。

1、首先看最后两个数4, 5。 它们的全排列为4 5和5 4, 即以4开头的5的全排列和以5开头的4的全排列。

由于一个数的全排列就是其本身，从而得到以上结果。

2、再看后三个数3, 4, 5。它们的全排列为3 4 5、3 5 4、 4 3 5、 4 5 3、 5 3 4、 5 4 3 六组数。

即以3开头的和4,5的全排列的组合、以4开头的和3,5的全排列的组合和以5开头的和3,4的全排列的组合.

从而可以推断，设一组数p = {r1, r2, r3, ... ,rn}, 全排列为perm(p)，pn = p - {rn}。

因此perm(p) = r1perm(p1), r2perm(p2), r3perm(p3), ... , rnperm(pn)。当n = 1时perm(p} = r1。

为了更容易理解，将整组数中的所有的数分别与第一个数交换，这样就总是在处理后n-1个数的全排列。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

class Solution { public:     vector<vector<int>> permute(vector<int>& nums) {         vector<bool> t(nums.size(),false);         vector<vector<int>> results;         helper(results, 0, nums);         return results;     }           void helper(vector<vector<int>> & results,int begin, vector<int> & nums){         if(begin == nums.size() - 1){             results.push_back(nums);             return;         }                   for(int i = begin; i < nums.size(); ++i){             swap(nums[begin], nums[i]);             helper(results, begin + 1, nums);             swap(nums[begin], nums[i]);         }     } };

另一种写法：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

class Solution { public:     vector<vector<int>> permute(vector<int>& nums) {         vector<bool> t(nums.size(),false);         vector<vector<int>> results;         helper(results, 0, nums);         return results;     }            void helper(vector<vector<int>> & results,int begin, vector<int> nums){         if(begin == nums.size() - 1){             results.push_back(nums);             return;         }                    for(int i = begin; i < nums.size(); ++i){             swap(nums[begin], nums[i]);             helper(results, begin + 1, nums);         }     } };

如果想要生成从小到大的全排列，使用如下写法：

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

class Solution { public:     vector<vector<int>> permute(vector<int>& nums) {         vector<vector<int>> results;         sort(nums.begin(), nums.end());         helper(results, nums, 0);         return results;     }           void helper(vector<vector<int>>& results,       /**< all the permutations. */                 vector<int> nums,                   /**< input number array. */                 int pos)                            /**< current position. */     {         if(nums.size() - 1 == pos){             results.push_back(nums);             return;         }         // from pos, swap every number in the array after pos(include pos itself)         for(int i = pos; i < nums.size(); ++i){             std::swap(nums[pos], nums[i]);             helper(results, nums, pos + 1);         }     } };

null