从中序表达式到逆序表达式（逆波兰式）（四则运算表达式求值）

本份代码需要两个栈。一个是符号栈，一个是数字栈。

输入中序表达式如9+(3-1)*3+10/2#

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<math.h>
#define max 100
char ex[max];        /*存储后序表达式*/
/*函数功能：将中序表达式转化为后序表达式*/
void trans() {
	char str[max];   /*表达式字符串*/
	char stack[max]; /*运算符栈*/
	char ch;         /*当前字符*/
	int sum, i, j, t, top = 0; /*sum用来统计字符串的长度*/
	/*t是数字栈栈顶指针*/
	/*top是数字栈栈顶指针*/
	printf("*****************************************
");
	printf("*输入一个求值的表达式，以#结束。*
");
	printf("******************************************
");
	printf("算数表达式：");
	i = 0;
	/*这个循环语句，获取一个用户输入的合法的表达式*/
	do {
		i++;
		scanf("%c", &str[i]);
	} while (str[i] != '#' && i != max);
	sum = i;
	t = 1;
	i = 1;
	ch = str[i];
	i++;
	//while循环，当前的字符不是#
	while (ch != '#') {
		//将该字符与运算符栈顶的运算符的优先关系相比较。
		//如果该字符优先关系高于此运算符栈顶的运算符，则将该运算符入栈。
		//括号的运算优先级高。
		switch (ch) {
		case '(':            /*判定为左括号，入符号栈*/
			top++;           /*栈顶指针+1*/
			stack[top] = ch;
			break;
		case ')': /*判定为右括号*/
			while (stack[top] != '(') {
				ex[t] = stack[top];/*把符号栈的栈顶元素压入另一个栈中*/
				top--;             /*符号栈的栈顶指针-1*/
				t++;               /*数字栈的栈顶指针+1*/
			}
			top--;
			break;
		case '+': /*判定为加减号*/
		case '-':
			while (top != 0 && stack[top] != '(') {
				ex[t] = stack[top];/*把符号栈的栈顶元素压入数字栈中*/
				top--;             /*符号栈的栈顶指针-1*/
				t++;               /*数字栈的栈顶指针+1*/
			}
			top++;
			stack[top] = ch;       /*不执行那个while循环的话，直接压入符号栈*/
			break;
		case '*': /*判定为乘除号*/
		case '/':
			while (stack[top] == '*' || stack[top] == '/') {
				ex[t] = stack[top];/*把符号栈的栈顶元素压入数字栈中*/
				top--;             /*符号栈的栈顶指针-1*/
				t++;               /*数字栈的栈顶指针+1*/
			}
			top++;
			stack[top] = ch;
			break;
		case ' ':/*滤去空格*/
			break;
		default:/*默认直接把数字压入数字栈*/
			while (ch >= '0' && ch <= '9') { /*判定为数字*/
				ex[t] = ch;                  /*把数字压入数字栈*/
				t++;                         /*数字栈栈顶指针+1*/
				/*这边的代码写得很巧妙*/
				ch = str[i];                 /*从字符串中取一个字符*/
				i++;                         /*字符数组下标+1*/
			}
			i--;
			ex[t] = '#';                     /*为每个数字加一个分隔符*/
			t++;
		}
		ch = str[i];
		i++;
	}
	/*把符号栈剩下的元素压进去*/
	while (top != 0) {
		ex[t] = stack[top];
		t++;
		top--;
	}
	ex[t] = '#';
	printf("
原来的中序表达式：");
	for (j = 1; j < sum; j++)
		printf("%c", str[j]);
	printf("
后缀表达式：");
	for (j = 1; j < t; j++)
		printf("%c", ex[j]);
}
void compvalue() { /*计算后缀表达式的值*/
	float stack[max], d; /*作为栈使用*/
	char ch;
	int t = 1, top = 0; /*t为ex下标，top为stack下标*/
	ch = ex[t];
	t++;
	//从左到右检查字符串
	while (ch != '#') {/*滤去#*/
		switch (ch) {
			//发现运算符，用栈顶的两个元素进行运算。
		case '+':
			stack[top - 1] = stack[top - 1] + stack[top];
			top--;
			break;
		case '-':
			stack[top - 1] = stack[top - 1] - stack[top];
			top--;
			break;
		case '*':
			stack[top - 1] = stack[top - 1] * stack[top];
			top--;
			break;
		case '/':
			if (stack[top] != 0)
				stack[top - 1] = stack[top - 1] / stack[top];
			else {
				printf("
	除零错误!
");
				//exit(0);                   /*异常退出*/
			}
			top--;
			break;
		default:
			d = 0;
			while (ch >= '0' && ch <= '9') {
				d = 10 * d + ch - '0'; /*将数字字符转化为对应的数值*/
				ch = ex[t];
				t++;
			}
			top++;
			stack[top] = d;
		}
		ch = ex[t];
		t++;
	}
	printf("
	计算结果:%g
", stack[top]);
}
int main() {
	trans();      //转化成逆波兰式
	compvalue();  //计算值
	return 0;
}

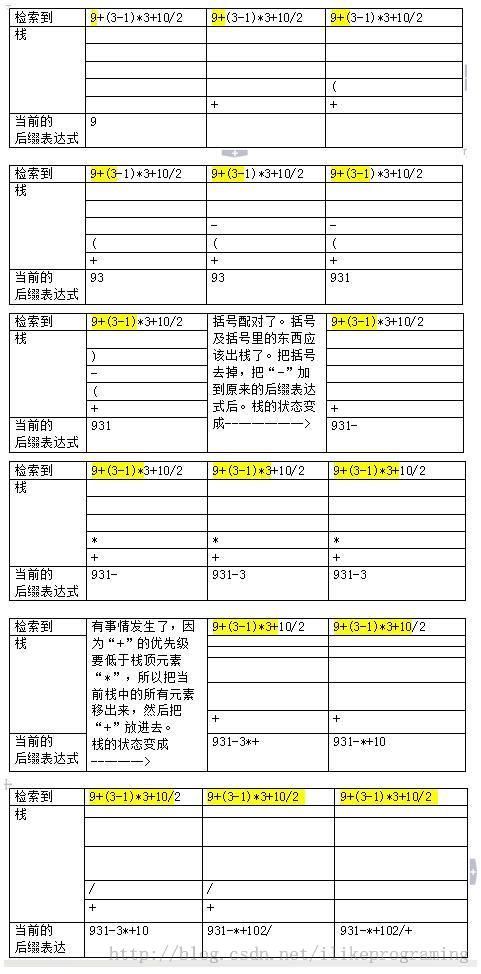
计算过程

来自为知笔记(Wiz)

附件列表

• 20131202195444703.jpg
• 20140101130903187.jpg