二叉树遍历

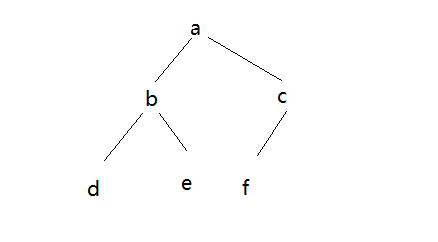
概念

二叉树的遍历有 先序、中序、后续遍历

• 先序遍历
  当前节点 - 左子节点 - 右子节点
  a-b-d-e-c-f
• 中序遍历
  左子节点 - 当前节点 - 右子节点
  d-b-e-a-f-c
• 后续遍历
  左子节点 - 右子节点 - 当前节点
  d-e-b-f-c-a

递归方式遍历

这种方式比较简单

// 先序遍历
public static List visitBefore(BinaryNode root)
{
    List list = new ArrayList<>();
    if (root == null)
    {
        return new ArrayList<>();
    }
    list.add(root.getData());
    // 遍历左子树
    list.addAll(visitBefore(root.getLeft()));
    // 遍历右子树
    list.addAll(visitBefore(root.getRight()));
    return list;
}

// 中序遍历
public static List visitMiddle(BinaryNode root)
{
    List list = new ArrayList<>();
    if (root == null)
    {
        return new ArrayList<>();
    }
    // 遍历左子树
    list.addAll(visitMiddle(root.getLeft()));
    list.add(root.getData());
    // 遍历右子树
    list.addAll(visitMiddle(root.getRight()));
    return list;
}
// 后序遍历
public static List visitAfter(BinaryNode root)
{
    List list = new ArrayList<>();
    if (root == null)
    {
        return new ArrayList<>();
    }
    // 遍历左子树
    list.addAll(visitAfter(root.getLeft()));
    // 遍历右子树
    list.addAll(visitAfter(root.getRight()));
    list.add(root.getData());
    return list;
}

非递归方式遍历

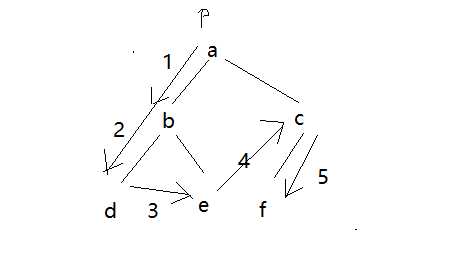
使用P指针，指向root节点。用P来画个轨迹，遍历整个二叉树。

1. 如果P有左子节点，将P入栈，P指向它的左子节点，该次循环结束
2. 如果P有没有左子节点，有右子节点，P指向它的右子节点
3. 如果P没有左子节点、也没有右子节点，说明已经走到了左下角。
   开始回溯，从栈中寻找有右子节点的元素，并将P指向右子节点
   P的运动轨迹为：
   

// 非递归遍历，中序遍历
public static List visitStackMiddle(BinaryNode root)
{
    List list = new ArrayList<>();
    BinaryNode p = root;
    SeqStack<BinaryNode> stack = new SeqStack<>();
    while (p != null)
    {
        if (p.getLeft() != null) // 1.如果有左子节点，P节点入栈
        {
            stack.push(p);
            p = p.getLeft();
        }
        else // 2. 如果没有左子节点
        {
            // 2.1 访问当前节点
            list.add(p.getData());

            if (p.getRight() != null) // 如果有右子节点，访问右节点
            {
                p = p.getRight();
            }
            else  // 若没有右节点，寻找栈顶元素直到找到有右节点的元素
            {
                while (!stack.empty() && stack.top().getRight() == null)  // 栈顶元素没有右节点，直接访问
                {
                    list.add(stack.pop().getData());
                }
                if (stack.empty())
                {
                    break;
                }
                // 输出栈顶元素
                list.add(stack.top().getData());
                p = stack.pop().getRight();
            }
        }
    }

    return list;
}

// 非递归遍历，先序遍历
public static List visitStackBefore(BinaryNode root)
{
    List list = new ArrayList<>();
    BinaryNode p = root;
    SeqStack<BinaryNode> stack = new SeqStack<>();
    while (p != null)
    {
        // 先序遍历，首先输出当前节点
        list.add(p.getData());
        if (p.getLeft() != null) // 1.如果有左子节点，P节点入栈
        {
            stack.push(p);
            p = p.getLeft();
        }
        else // 2. 如果没有左子节点
        {

            if (p.getRight() != null) // 如果有右子节点，访问右节点
            {
                p = p.getRight();
            }
            else  // 若没有右节点，寻找栈顶元素直到找到有右节点的元素
            {
                while (!stack.empty() && stack.top().getRight() == null)  // 栈顶元素没有右节点，直接访问
                {
                    stack.pop().getData();
                }
                if (stack.empty())
                {
                    break;
                }
                // 输出栈顶元素
                p = stack.pop().getRight();
            }
        }
    }

    return list;
}

// 非递归遍历，后序遍历
public static List visitStackAfter(BinaryNode root)
{
    List list = new ArrayList<>();
    BinaryNode p = root;
    SeqStack<BinaryNode> stack = new SeqStack<>();
    BinaryNode last = null;
    while (p != null)
    {
        if (p.getLeft() != null) // 1.如果有左子节点，P节点入栈
        {
            stack.push(p);
            p = p.getLeft();
        }
        else // 2. 如果没有左子节点
        {
            if (p.getRight() != null) // 如果有右子节点，访问右节点
            {
                last = p;  // P节点未访问，需要寄存
                p = p.getRight();
            }
            else  // 若没有右节点，寻找栈顶元素直到找到有右节点的元素
            {
                // 访问当前元素
                list.add(p.getData());  // 访问数据位置
                while (!stack.empty() && stack.top().getRight() == null)  // 栈顶元素没有右节点，直接访问
                {
                    // 如果栈顶元素没有右节点，直接访问，并弹出
                    list.add(stack.pop().getData());
                }
                if (stack.empty())
                {
                    break;
                }
                if (last != null)
                {
                    list.add(last.getData());
                }
                // 使用寄存器 存储上一个中间值
                last = stack.top();
                // 输出栈顶元素
                p = stack.pop().getRight();
            }
        }
    }
    if (last != null)
    {
        list.add(last.getData());
    }

    return list;
}

逐层遍历

使用队列，比较简单。

// 层次遍历
public static List visitLayer(BinaryNode root)
{
    List list = new ArrayList<>();
    // 定义一个队列
    Queue<BinaryNode> queue = new LinkedBlockingDeque<>();
    if (root == null)
    {
        return new ArrayList<>();
    }
    queue.add(root);
    while (!queue.isEmpty())
    {
        // 处理一层,将队列中的所有元素逐个出列，并把该元素的子节点加入队列汇总
        int size = queue.size();
        for (int i = 0; i < size; i++)
        {
            BinaryNode peek = queue.poll();
            list.add(peek.getData());
            if (peek.getLeft() != null)
            {
                queue.add(peek.getLeft());
            }
            if (peek.getRight() != null)
            {
                queue.add(peek.getRight());
            }
        }

    }
    return list;
}