目录
what's the 数据结构
数据结构是指相互之间存在着一种或多种关系的数据元素的集合和该集合中数据元素之间的关系组成。 简单来说,数据结构就是设计数据以何种方式组织并存储在计算机中。 比如:列表、集合与字典等都是一种数据结构。
通常情况下,精心选择的数据结构可以带来更高的运行或者存储效率。数据结构往往同高效的检索算法和索引技术有关。
数据结构按照其逻辑结构可分为线性结构、树结构、图结构:
-
- 线性结构:数据结构中的元素存在一对一的相互关系
- 树结构:数据结构中的元素存在一对多的相互关系
- 图结构:数据结构中的元素存在多对多的相互关系
下面我来重点来学习数据结构中比较重要的几种:栈、队列、链表、哈希表、二叉搜索树
栈
栈(Stack)是一个数据集合,它是一种运算受限的线性表。其限制是仅允许在表的一端进行插入和删除运算。这一端被称为栈顶,相对地,把另一端称为栈底。可以将栈理解为只能在一端进行插入或删除操作的列表。
栈的特点:后进先出、先进后出(类似于往箱子里放东西,要拿的时候只能拿最上面的而最上面的是最后进的)
栈操作:进栈push、出栈pop、取栈顶gettop(在Python中,不用自定义栈,直接用列表就行,进栈函数:append 出栈函数:pop 查看栈顶函数:li[-1])
栈的应用
栈可以应用在处理括号匹配问题——括号匹配问题:给一个字符串,其中包含小括号、中括号、大括号,求该字符串中的括号是否匹配。
基本思路:按顺序遍历字符串是左括号则进栈,来的是右括号则将栈顶左括号pop,若来的右括号与栈顶左括号不匹配或空栈情况下来了右括号则返回错误信息
def brace_match(s): stack = [] match = {')':'(', ']':'[', '}':'{'} match2 = {'(':')', '[':']', '{':'}'} for ch in s: if ch in {'(', '[', '{'}: stack.append(ch)#左括号入栈 elif len(stack) == 0: print("缺少%s" % match[ch])#栈空了,但却来了一个右括号 return False elif stack[-1] == match[ch]:#栈顶左括号与来的右括号相匹配 stack.pop()#出栈 else: print("括号不匹配") return False if len(stack) > 0:#全部操作完后栈内还有剩余左括号 print("缺少%s" % (match2[stack[-1]]))#显示栈顶左括号对应的右括号 return False print('合法') return True brace_match("[{()[]}{}{}")#缺少]
队列
队列(Queue)是一个数据集合,仅允许在列表的一端进行插入,另一端进行删除。 进行插入的一端称为队尾(rear),插入动作称为进队或入队;进行删除的一端称为队头(front),删除动作称为出队。和栈一样,队列是一种操作受限制的线性表。
队列的性质:先进先出(可以将队列理解为排队买东西)
特殊情况——双向队列:队列的两端都允许进行进队和出队操作。
如何用列表实现队列:
- 初步设想:列表+两个下标指针
- 创建一个列表和两个变量,front变量指向队首,rear变量指向队尾。初始时,front和rear都为0。
- 进队操作:元素写到li[rear]的位置,rear自增1。
- 出队操作:返回li[front]的元素,front自减1。
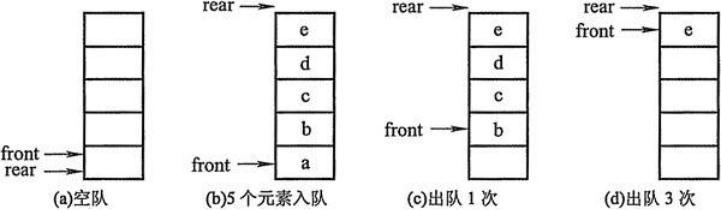
以上就是队列实现的基本思路,但是其实队列的实现原理是一个环形队列
环形队列:当队尾指针front == Maxsize + 1时,再前进一个位置就自动到0。
- 实现方式:求余数运算
- 队首指针前进1:front = (front + 1) % MaxSize
- 队尾指针前进1:rear = (rear + 1) % MaxSize
- 队空条件:rear == front
- 队满条件:(rear + 1) % MaxSize == front
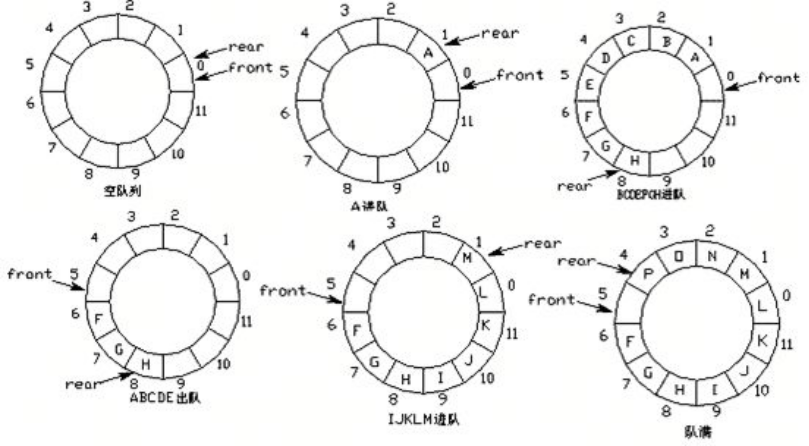
在Python中,有一个内置模块可以帮我们快速建立起一个队列——deque模块
""" 使用方法:from collections import deque 创建队列:queue = deque(li) 进队:append() 出队:popleft() 双向队列队首进队:appendleft() 双向队列队尾进队:pop() """
栈和队列的知识点应用:
用栈和队列的知识来解决迷宫问题:http://www.cnblogs.com/zhuminghui/p/8414307.html
链表
链表中每一个元素都是一个对象,每个对象称为一个节点,包含有数据域key和指向下一个节点的指针next。通过各个节点之间的相互连接,最终串联成一个链表。
#结点的定义 class Node(object): def __init__(self, item): self.item = item self.next = None

建立链表的方式有头插法和尾插法两种
- 头插法:在一个结点的前面插入元素,head的指针由指向原来的结点变为指向新元素,新元素的指针指向原来的结点
- 尾插法:在一个元素后面插入一个元素,原来结点的指针指向新元素
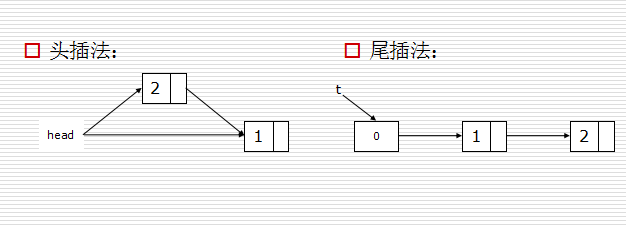
建立列表实现代码如下:
#定义结点 class Node: def __init__(self, data): self.data = data self.next = None #头插法 def create_linklist(li): head = None for num in li: node = Node(num) node.next = head head = node return head #尾插法 def create_linklist_tail(li): head = None if not li: return head head = Node(li[0]) tail = head for num in li[1:]: node = Node(num) tail.next = node tail = node return head def print_linklist(head): node = head while node: print(node.data) node = node.next linklist = create_linklist_tail([1,2,3,4]) print_linklist(linklist)
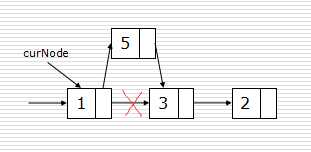
#curNode为A结点 c.next = curNode.next curNode.next = c
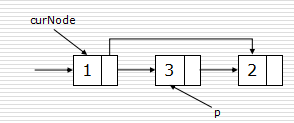
#p为要删除的结点 p = curNode.next curNode.next = curNode.next.next#即p.next del p
class Node(object): def __init__(self, item=None): self.item = item self.next = None self.prior = None
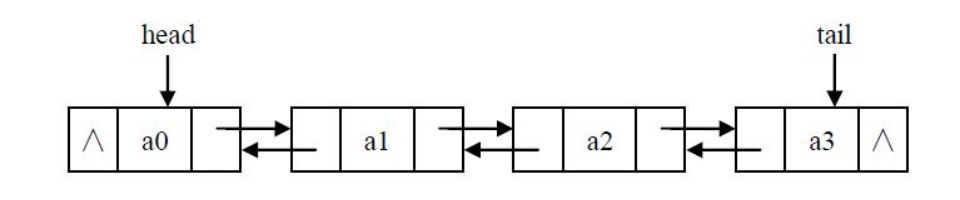
双向链表结点的插入
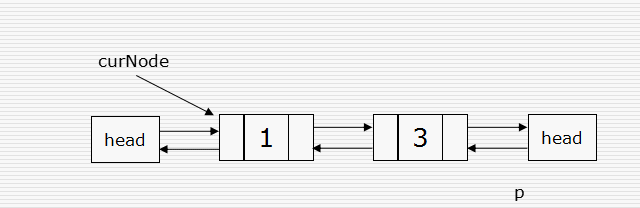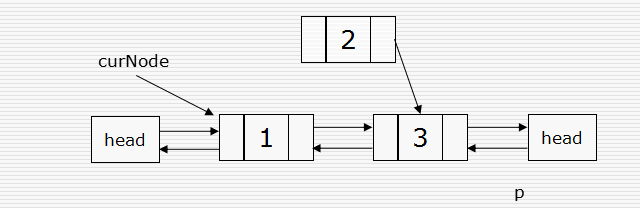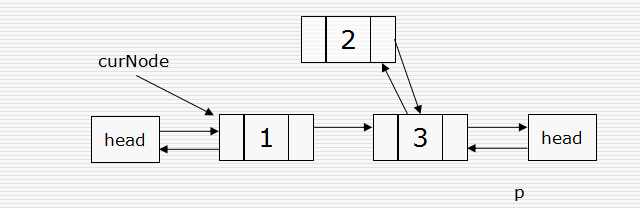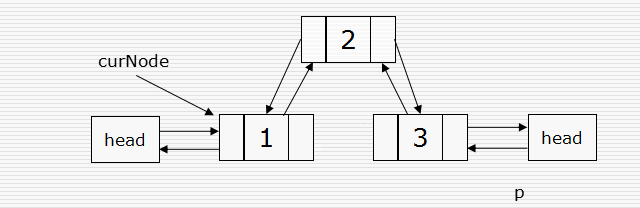
#p为新插入的元素 p.next = curNode.next curNode.next.prior = p p.prior = curNode curNode.next = p
#p为要删除的结点 p = curNode.next curNode.next = p.next p.next.prior = curNode del p
- 按元素值查找——O(n),因为没有下标所以没法做二分
- 按下标查找——O(n),因为没有下标
- 在某元素后插入——O(1)
- 删除某元素——O(1)
哈希表(Hash Table,又称为散列表),是一种线性表的存储结构。哈希表由一个顺序表(数组)和一个哈希函数组成。哈希函数h(k)将元素k作为自变量,返回元素的存储下标。
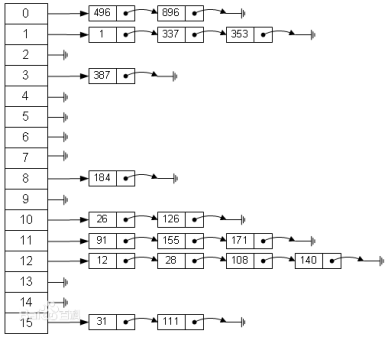
假设有一个长度为7的数组,哈希函数h(k)=k%7。元素集合{14,22,3,5}的存储方式如下图。

哈希冲突:
由于哈希表的大小是有限的,而要存储的值的总数量是无限的,因此对于任何哈希函数,都会出现两个不同元素映射到同一个位置上的情况,这种情况叫做哈希冲突。
比如上图中的哈希表就存在这哈希冲突——h(k)=k%7, h(0)=h(7)=h(14)=...
- 线性探查:如果位置i被占用,则探查i+1, i+2,……
- 二次探查:如果位置i被占用,则探查i+12,i-12,i+22,i-22,……
- 二度哈希:有n个哈希函数,当使用第1个哈希函数h1发生冲突时,则尝试使用h2,h3,……
哈希表在Python中的应用
#字典与集合都是通过哈希表来实现的 #在Python中的字典: a = {'name': 'Damon', 'age': 18, 'gender': 'Man'} #使用哈希表存储字典,通过哈希函数将字典的键映射为下标。假设h(‘name’) = 3, h(‘age’) = 1, h(‘gender’) = 4,则哈希表存储为[None, 18, None, ’Damon’, ‘Man’] #在字典键值对数量不多的情况下,几乎不会发生哈希冲突,此时查找一个元素的时间复杂度为O(1)。