Wall
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 41143 | Accepted: 14068 |
Description
Once upon a time there was a greedy King who ordered his chief Architect to build a wall around the King's castle. The King was so greedy, that he would not listen to his Architect's proposals to build a beautiful brick wall with a perfect shape and nice tall towers. Instead, he ordered to build the wall around the whole castle using the least amount of stone and labor, but demanded that the wall should not come closer to the castle than a certain distance. If the King finds that the Architect has used more resources to build the wall than it was absolutely necessary to satisfy those requirements, then the Architect will loose his head. Moreover, he demanded Architect to introduce at once a plan of the wall listing the exact amount of resources that are needed to build the wall.

Your task is to help poor Architect to save his head, by writing a program that will find the minimum possible length of the wall that he could build around the castle to satisfy King's requirements.
The task is somewhat simplified by the fact, that the King's castle has a polygonal shape and is situated on a flat ground. The Architect has already established a Cartesian coordinate system and has precisely measured the coordinates of all castle's vertices in feet.

Your task is to help poor Architect to save his head, by writing a program that will find the minimum possible length of the wall that he could build around the castle to satisfy King's requirements.
The task is somewhat simplified by the fact, that the King's castle has a polygonal shape and is situated on a flat ground. The Architect has already established a Cartesian coordinate system and has precisely measured the coordinates of all castle's vertices in feet.
Input
The first line of the input file contains two integer numbers N and L separated by a space. N (3 <= N <= 1000) is the number of vertices in the King's castle, and L (1 <= L <= 1000) is the minimal number of feet that King allows for the wall to come close to the castle.
Next N lines describe coordinates of castle's vertices in a clockwise order. Each line contains two integer numbers Xi and Yi separated by a space (-10000 <= Xi, Yi <= 10000) that represent the coordinates of ith vertex. All vertices are different and the sides of the castle do not intersect anywhere except for vertices.
Next N lines describe coordinates of castle's vertices in a clockwise order. Each line contains two integer numbers Xi and Yi separated by a space (-10000 <= Xi, Yi <= 10000) that represent the coordinates of ith vertex. All vertices are different and the sides of the castle do not intersect anywhere except for vertices.
Output
Write to the output file the single number that represents the minimal possible length of the wall in feet that could be built around the castle to satisfy King's requirements. You must present the integer number of feet to the King, because the floating numbers are not invented yet. However, you must round the result in such a way, that it is accurate to 8 inches (1 foot is equal to 12 inches), since the King will not tolerate larger error in the estimates.
Sample Input
9 100 200 400 300 400 300 300 400 300 400 400 500 400 500 200 350 200 200 200
Sample Output
1628
Hint
结果四舍五入就可以了
Source
思路:就是用所有点构成的凸包,然后将凸包向外推L米就可以了,可以知道将墙直接外推L米,墙的长度没变,但是两堵墙之间会有缝隙,这个如果用直线相连
就会浪费,所以直接用圆弧相连,半径为L,所以:总长度 = 原凸包周长 + 所有圆弧的长度。其实所有圆弧的长度之和会构成一个半径为L的圆,所以最后的结果: 总长度 = 原凸包周长 + 圆的周长(R=L)。关于为什么所有圆弧会拼成一个原,我一也是看了许多博客慢慢理解的,证明如下:
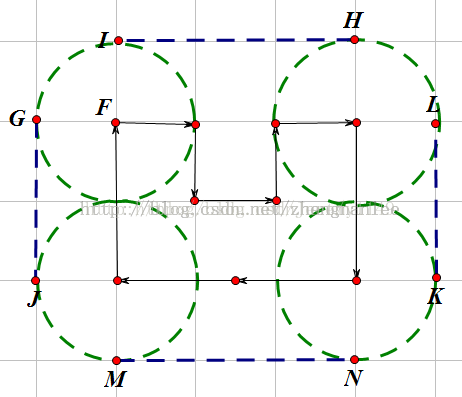
证明:

先从简单的例子看起:假设现在的凸包有四个顶点构成,可以就一个顶点来观察,我们可以看到此处的周角由四个部分组成:2个直角,一个凸包内角,一个圆弧对应的圆心角。
同理每个顶点都有类似的关系,同时周角固定为360度,而凸包内角和为(4-2)*180 ;
所以总的圆弧对应的圆心角 = 4个周角 - 4 * 2个直角 - 4个凸包内角 = 4 * 360 - 4 * 2 * 90 - (4-2)*180 = 1440-720-360 =360度。
现在推广到n个顶点的凸包:
则所有内角和 = 周角 * n - n * 2个直角 - (n-2)*180 = 360*n - n *180 - n*180 + 360 = 360度。
故对于任意的凸包,所有的圆弧对应的圆心角之和都为360度,它们构成一个完整的圆。
ac代码如下:
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;
#define N 10005
const double PI = acos(-1.0);
int n,tot;//n为二维平面上点的个数,tot为凸包上点的个数
struct node {
int x,y;
}a[N],p[N]; //p[]用来储存凸包
double dis(node a1,node b1){ //两点间距离公式
return sqrt((a1.x-b1.x)*(a1.x-b1.x)+(a1.y-b1.y)*(a1.y-b1.y) + 0.00);
}
//叉积:返回结果为正说明p2在向量p0p1的左边(三点构成逆时针方向);
//为负则相反;为0则三点共线(叉积的性质很重要)
double multi(node p0,node p1,node p2){ //
return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
}
//极角排序:极角排序是根据坐标系内每一个点与x轴所成的角,逆时针比较。按照角度从小到大的方式排序
int cmp(node p1,node p2){ //极角排序;
int x=multi(p1,p2,a[0]);
if(x>0||(x==0&&dis(p1,a[0])<dis(p2,a[0])))
return 1;
return 0;
}
void Graham(){ //求凸包
int k=0;
for(int i=0;i<n;i++) //找到最下最左的一个点
if(a[i].y<a[k].y||(a[i].y==a[k].y&&a[i].x<a[k].x))
k=i;
swap(a[0],a[k]); //将其设置为第一个点
sort(a+1,a+n,cmp);
tot=2,p[0]=a[0],p[1]=a[1]; //p[]模拟栈,用来储存凸包
for(int i=2;i<n;i++){
while(tot>1&&multi(p[tot-1],p[tot-2],a[i])>=0)
tot--; //右拐就回退
p[tot++]=a[i]; //左拐就放入
}
}
double getArea(){
struct node b[3];
b[0] = p[0], b[1] = p[1], b[2] = p[2];
double area = 0;
for(int i = 2; i < tot; i++){
area += multi(b[0], b[1], p[i]) / 2.0;
b[1] = p[i];
}
return area;
}
double getGirth(){
double rt = 0;
for(int i = 0; i < tot; i++){
rt += dis(p[i], p[(i+1)%tot]);
}
return rt;
}
int main(){
double L;
while(cin >> n >> L){
tot = 0;
for(int i = 0; i < n; i++){
cin >> a[i].x >> a[i].y;
}
Graham();
double res = getGirth();
res += 2*PI*L;
cout << int(res + 0.5) << endl;
}
return 0;
}