12-凸包模板-计算几何

先说我对找凸包上的点时的理解： 
P,A,B三个点，通过叉乘可以得知P,A,B的位置关系 
AB × AP = |AB| * |AP| * sin∠PAB. 
方向是A到B，A到P。 
如果>0,那就是P在线AB左边,<0就是在右边，=0就是在线上。 
为什么可以这样判断呢，AB × AP = |AB| * |AP| * sin∠PAB P在AB的左边，则∠PAB在0°到180°之间 sin∠PAB > 0 P在AB右边时，则∠PAB在-180°到0°之间 sin∠PAB < 0 因此，我们只要用AB和AP的叉积的正负，就可以判断P和AB的相对位置(AP相对AB是顺时针还是逆时针旋转)。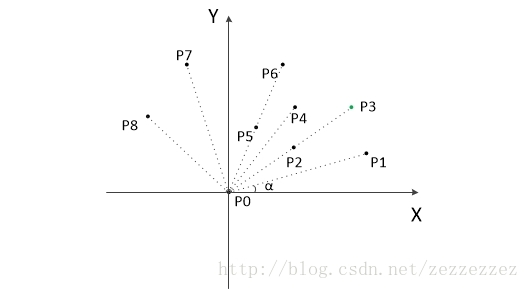 
 
这里我想说一下我的理解吧。 
为什么说一个点在线的左边就是凸包上的点呢，这个要先规定线的方向，当方向确定才能去说左边，右边。因为p0是最下边的点，通过极角排序后，咱们从X正半轴向上扫，注意叉乘公式，这个公式给了点之间的方向。所以这时候都是以左边称。一个三角形，只有一个点在所有边的左边才能定这个点在凸包内。那出现一个右边的点那就不行。举例来说有很多点，p0,p1,p2,p3…. 
当你知道了p0,p1是凸包上的点，通过计算发现p2在线p0p1的左边，此时线p0p1的右边是没有点的，当你手绘凸包时，线p0p1右边没有了点，那么当前知道的它左边的点就是凸包上的点，我管这个点叫凸包待定点，因为目前只计算了p2，通过计算p2的下一个点p3可以验证p2到底是不是凸包确定点。 

总结：就是先逆时针排序，选取最下最左的点为第一个点，然后按顺序取点，左拐就放入，继续走，右拐则就要回退，一直退到左拐为止。

#define N 10005 

int n,tot;//n为二维平面上点的个数，tot为凸包上点的个数  
struct node  {  
    int x,y;  
}a[N],p[N]; //p[]用来储存凸包

double dis(node a1,node b1){  //两点间距离公式 
    return (a1.x-b1.x)*(a1.x-b1.x)+(a1.y-b1.y)*(a1.y-b1.y);  
} 

//叉积：返回结果为正说明p2在向量p0p1的左边（三点构成逆时针方向）；
//为负则相反；为0则三点共线(叉积的性质很重要)
double multi(node p0,node p1,node p2){ // 
    return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);  
}  

//极角排序：极角排序是根据坐标系内每一个点与x轴所成的角，逆时针比较。按照角度从小到大的方式排序
int cmp(node p1,node p2){  //极角排序；
    int x=multi(p1,p2,a[0]);  
    if(x>0||(x==0&&dis(p1,a[0])<dis(p2,a[0]))) 
		return 1;  
    return 0;  
} 

void Graham(){  //求凸包 
    int k=0;          
    for(int i=0;i<n;i++)   //找到最下最左的一个点 
        if(a[i].y<a[k].y||(a[i].y==a[k].y&&a[i].x<a[k].x)) 
			k=i;  
    swap(a[0],a[k]);       //将其设置为第一个点 
    sort(a+1,a+n,cmp);     
    tot=2,p[0]=a[0],p[1]=a[1];  //p[]模拟栈，用来储存凸包
    for(int i=2;i<n;i++){  
        while(tot>1&&multi(p[tot-1],p[tot-2],a[i])>=0) 
			tot--;     //右拐就回退 
        p[tot++]=a[i]; //左拐就放入  
    }  
}  

double getArea(){
	struct node b[3];
	b[0] = p[0], b[1] = p[1], b[2] = p[2];
	double area = 0;
	for(int i = 2; i < tot; i++){
		area += multi(b[0], b[1], p[i]) / 2.0;
		b[1] = p[i];
	}
	return area;
}