链接:https://www.nowcoder.com/acm/contest/80/B
来源:牛客网
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 262144K,其他语言524288K
64bit IO Format: %lld
空间限制:C/C++ 262144K,其他语言524288K
64bit IO Format: %lld
题目描述
在文某路学车中学高一新生军训中,Jxc正站在太阳下站着军姿,对于这样的酷热的阳光,Jxc 表示非常不爽。
Jxc将天空看做一个n*n的矩阵,此时天上有m朵云,这些云会随机分布在m个不同的位置,同时太阳会随机出现在一个位置,Jxc想知道他被太阳晒到的概率是多少,由于他仍在站军姿,所以这个有趣的问题就交给了你。考虑到精度问题,Jxc只需要知道这个概率在对998244353取模意义下的值。
Tips:一个分数p/q在模意义下的值即p*q-1在模意义下的值,Xp-11 (mod p)
输入描述:
输入只有一行,包含两个整数n、m。n和m的意义见题面.
输出描述:
第一行包含一个整数Ans,为答案
示例1
输入
2 2
输出
499122177
备注:
1 <= n, m <= 2000,m <=n^2

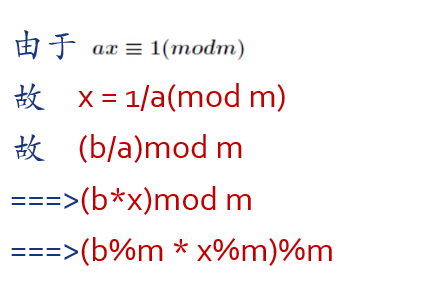
#include <bits/stdc++.h>
using namespace std;
const int mod = 998244353;
long long quai(int n, int q){
long long ans = 1, jie = n;
while(q){
if(q & 1){
ans = (ans * jie) % mod;
}
jie = (jie * jie) % mod;
q = q >> 1;
}
return ans;
}
int main(){
long long n;
int m;
int b;
cin >> n >> m;
b = n * n - m;
long long x = quai(n * n, mod - 2);
// cout << x << endl;
cout << ((b % mod) * (x % mod)) % mod << endl;
return 0;
}