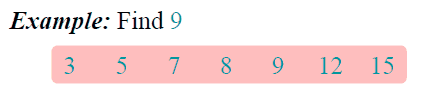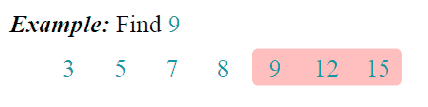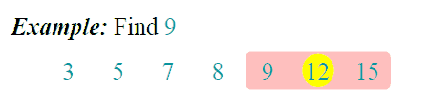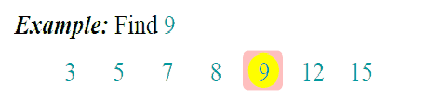算法

文章目录

• 算法
• 排序算法介绍
• 常见的排序算法
• 基于O(N^2)比较的排序算法
• 冒泡排序
• 分析
• 提前终止
• python代码举例
• 选择排序
• 分析
• python代码举例
• 插入排序
• 分析
• 举例
• O(N log N)基于比较的排序
• 快速排序
• 分析
• python代码举例
• 算法之二分法查找
• 思想
• 思路

算法

个人简单的理解,有很多不足的地方,希望能够帮助到大家

排序算法介绍

排序是一个非常经典的问题，它以一定的顺序对一个数组（或一个列表）中的项进行重新排序（可以进行比较，例如整数，浮点数，字符串等）（增加，非递减，递减， 增加，词典等）。
有许多不同的排序算法，每个都有其自身的优点和局限性。
排序通常被用作各种计算机科学课程中的介绍性问题，以展示一系列算法思想。

常见的排序算法

1. 基于比较的排序算法:
   1. BUB - 冒泡排序,
   2. SEL - 选择排序,
   3. INS - 插入排序,
   4. MER - 归并排序 (递归实现),
   5. QUI - 快速排序 (递归实现),
   6. R-Q - 随机快速排序 (递归实现).
2. 不基于比较的排序算法:
   1. COU - 计数排序,
   2. RAD - 基数排序.

下面将一一进行举例

基于O(N^2)比较的排序算法

在接下来的举例种，我们将讨论三种基于比较的排序算法

1. 冒泡排序
2. 选择排序
3. 插入排序

它们被称为基于比较的比较，因为它们比较数组的元素对并决定是否交换它们。
这三种排序算法最容易实现，但不是最有效的，因为它们的时间复杂度是O（N2)。

冒泡排序

给定一个N个元素的数组，冒泡法排序将：

1. 如果元素大小关系不正确，交换这两个数（在本例中为a> b），
2. 比较一对相邻元素（a，b），
3. 重复步骤1和2，直到我们到达数组的末尾（最后一对是第（N-2）和（N-1）项，因为我们的数组从零开始）
4. 到目前为止，最大的元素将在最后的位置。 然后我们将N减少1，并重复步骤1，直到N = 1。

如果您想象较大的项目“起泡”（也就是“浮动到数组的右侧”），则应该能想象到一个“气泡式”动画。

分析

比较和交换需要一个以常量为界的时间，我们称之为c。
（标准）Bubble Sort中有两个嵌套循环。
外循环正好运行N次迭代。 但内部循环运行变得越来越短：

1. 当 i = 0，（N-1）次迭代（比较和可能交换）时。
2. 当 i = 1，（N-2）次迭代时，…
3. 当 i =（N-2）时，1次迭代,
4. 当 i=（N-1），0迭代.

因此，总迭代次数=（N-1）+（N-2）+ … + 1 + 0 = N *（N-1）/ 2。
总时间= c * N *（N-1）/ 2 = O（N ^ 2）。

提前终止

冒泡排序实际上是低效的，它的 O(N^2) 时间复杂度。 想象一下，我们有 N = 106 个数字。 即使我们的计算机速度超快，并且可以在1秒内计算108次操作，但冒泡排序仍需要大约100秒才能完成。
但是，它可以提前终止，例如， [1,2,3,4,5]，它在O(N)时间结束。
改进的思路很简单：如果我们通过内部循环完全不交换，这意味着数组已经排序，我们可以在这个点上停止冒泡排序。

python代码举例

### 时间复杂度：最差的情况：O(n^2)  最好的情况：O(n)
def bubble_sort(li):
    #得到Li的全部索引
    for i in range(len(li)-1):
        flag = True #标识下面循环是否进行了交换,如果遍利一圈没有交换,说明Li已经是有序列表;则进入最后一步结束冒泡,时间复杂度为O(n)
        for j in range(len(li)-1-i):
            #将相邻的两个数进行比较,前面数字大于后面,则交换位置
            if li[j] > li[j+1]:
                li[j], li[j+1] = li[j+1], li[j]
                flag = False
        if flag:
            return
li = [1,3,4,2,6,5,8,7,9]
select_sort(li)
print(li)

选择排序

给定 N****L = 0

1. 在 [L … N-1] 范围内找出最小项目 X 的位置，
2. 用第 L 项交换X，
3. 将下限 L 增加1并重复步骤1直到 L = N-2。

别犹豫，让我们在上面的同一个小例子数组上尝试。在不失普遍性的情况下，我们也可以实现反向的选择排序：找到最大项目 的位置并将其与最后一个项目交换。

分析

假如有数组 li = [1,3,4,2,6,5,8,7,9]；我们先假设第一个数是最小的，然后将后面所有的数依次和这个比较，如果有比这个还小的数字，则进行位置交换，这样我们第一个数一定是最小的；每一次比较都会产生最小的数字，这些最小的数字不再参与下一次的比较。如果不太清晰，请看示例代码，可以自行Debug查看

python代码举例

### 时间复杂度是：O(n^2)
# li = [1,3,4,2,6,5,8,7,9]
def select_sort(li):
    for i in range(len(li)):
        minLoc = i #假设第一个数是最小的。经过比较后得到的最小数不参与后面的比较
        for j in range(i+1, len(li)):
            if li[minLoc] > li[j]:
                li[minLoc], li[j] = li[j], li[minLoc]
                
li = [1,3,4,2,6,5,8,7,9]
select_sort(li)
print(li)

一句话总结：每一次循环得出一个最小的数字，每次得到的最小数字不再参与比较，每次得到的最小数字依次往后放

插入排序

插排，插牌，还没打过牌，可以先去学习打牌。

插入排序类似于大多数人安排扑克牌的方式。[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pKxnX8pd-1586006110626)(https://puu.sh/vfi6a/e532309371.png)]

1. 从你手中的一张牌开始，
2. 选择下一张卡并将其插入到正确的排序顺序中，
3. 对所有的卡重复上一步。

分析

直接插入排序(Insertion Sort)的基本思想是：每次将一个待排序的记录，按其关键字大小插入到前面已经排好序的子序列中的适当位置，直到全部记录插入完成为止。

举例

### 时间复杂度是：O(n^2)
def insert_sort(li):
    for i in range(1, len(li)):  # i=1
        tmp = li[i]  #tmp:3
        j = i - 1  #j=1
        
        while j >= 0 and li[j] > tmp:
            li[j+1] = li[j]  
            j = j - 1   
        li[j+1] = tmp
        
li = [1,3,4,2,6,5,8,7,9]
insert_sort(li)
print(li)

一句话总结：学打牌

O(N log N)基于比较的排序

==注意：基于比较的排序中我只举例快排并且只写一种方式，因为头发要紧；==如果有兴趣研究，请点击查看其他几种排序

我们将在接下来的几张幻灯片中讨论两种（加一半）基于比较的排序算法：

1. 归并排序，
2. 快速排序和它的随机版本（只有一个变化）。

这些排序算法通常以递归方式实现，使用分而治之的问题解决范例，并且运行在合并排序和O（N log N）时间的**O（N log N）**时间中，以期望随机快速排序。
PS：尽管如此，快速排序（Quick Sort）的非随机版本在 O(N2) 中运行。

快速排序

快速排序是另一个–分而治之排序算法（另一个在这个可视化页面中讨论的是归并排序）。
我们将看到，这种确定性的，非随机化的快速排序的版本可能在对手输入中具有O（N2）的很差的时间复杂度，之后再继续–随机化的–和可用的版本。

分析

快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序。它采用了一种分治的策略，通常称其为分治法(Divide-and-ConquerMethod)。

该方法的基本思想是：

1．先从数列中取出一个数作为基准数。

2．分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边。

3．再对左右区间重复第二步，直到各区间只有一个数。

虽然快速排序称为分治法，但分治法这三个字显然无法很好的概括快速排序的全部步骤。因此我的对快速排序作了进一步的说明：挖坑填数+分治法：

划分步骤：选择一个项目 p（称为枢轴点）然后将 a[i…j] 的项目分为三部分：a [i…m-1]，a [m] 和 a[m + 1…j]。 a [i…m-1]（可能为空）包含小于 p 的项目。 a [m] 是枢轴点 p，例如：指数 m 是已排序数组 a 的排序顺序中 p 的正确位置。 a [m + 1…j]（可能为空）包含大于或等于 p 的项目。 然后，递归地对这两部分进行排序。
解决步骤：不要惊讶…我们什么都不做！
如果您将其与归并排序进行比较，您会发现快速排序的 D＆C 步骤与归并排序完全相反。

python代码举例

估计上面文字看了反而更懵，那么我们直接上代码，Debug走一下，再来做个总结

##### 时间复杂度是：O(nlogn)
# 归位函数
def partition(li, left, right):  #### O(n)
    tmp = li[left]
    while left < right:
        while left < right and li[right] >= tmp:
            right = right - 1
        li[left] = li[right]

        while left < right and li[left] <= tmp:
            left = left + 1
        li[right] = li[left]
    li[left] = tmp
    return left
#快排
def quick_sort(li, left, right):
    if left < right:
        mid = partition(li, left, right)  ### 归位函数
        quick_sort(li, left, mid-1)     #### O(logn)
        quick_sort(li, mid+1, right)
li = [5,7,4,6,3,8,2,9,1,9]
quick_sort(li)
print(li)

一句话总结：每一个作比较的基准数，必须同时满足，大于前面，小于后面；

如果我的解释不太清楚，那么可以参考一下其他网友的方法，CSDN，Visuglo动画展示

算法之二分法查找

二分查找算法也成为折半查找算法，是在有序数组中用到的较为频繁的一种查找算法。在未接触二分查找算法时，最常用的做法是，对数组进行遍历，跟每个元素进行比较，即顺序查找，当数据量很大的时候，顺序查找会很慢。而二分查找原理是，每一次比较都会缩小一半查找范围，大大节约了查找时间。

思想

二分查找算法是建立在有序数组基础上的。

1. 查找过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则查找过程结束；
2. 如果某一待查找元素大于或小于中间元素，则在数组大雨或小于中间元素的那一半中查找，查找方法跟上述一样。
3. 如果在某一步骤数组为空，则代表找不到

思路

1. 找出位于数组中间的值（为便于表述，将该值放在一个临时变量tmp中）。
2. 需要找到的key和tmp进行比较。
3. 如果key值大于tmp，则把数组中间位置作为下一次计算的起点；重复第1、2步骤继续查找。
4. 如果key值小于tmp，则把数组中间位置作为下一次计算的终点；重复第1、2步骤继续查找。
5. 如果key值等于tmp，则返回数组下标，完成查找。

咱传递的是思想，只要思想不滑坡，问题总比方法多，莱茨狗