《机器学习Python实现_01_线性模型_线性回归》

一.模型结构

线性回归算是回归任务中比较简单的一种模型，它的模型结构可以表示如下：

[f(x)=w^Tx^* ]

这里(x^*=[x^T,1]^T)，(xin R^n)，所以(win R^{n+1})，(w)即是模型需要学习的参数，下面造一些伪数据进行演示：

import numpy as np
#造伪样本
X=np.linspace(0,100,100)
X=np.c_[X,np.ones(100)]
w=np.asarray([3,2])
Y=X.dot(w)
X=X.astype('float')
Y=Y.astype('float')
X[:,0]+=np.random.normal(size=(X[:,0].shape))*3#添加噪声

Y=Y.reshape(100,1)

import matplotlib.pyplot as plt
%matplotlib inline
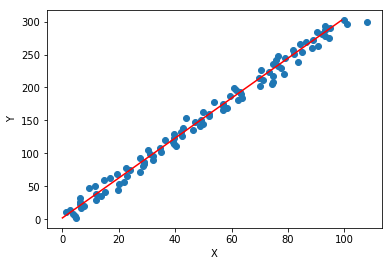
plt.scatter(X[:,0],Y)
plt.plot(np.arange(0,100).reshape((100,1)),Y,'r')
plt.xlabel('X')
plt.ylabel('Y')

Text(0,0.5,'Y')

二.损失函数

利用等式(y=3x+2)我造了一些伪数据，并给(x)添加了一些噪声数据，线性回归的目标即在只有(x,y)的情况下，求解出最优解：(w=[3,2]^T)；可以通过MSE（均方误差）来衡量(f(x))与(y)的相近程度：

[L(w)=sum_{i=1}^m(y_i-f(x_i))^2=sum_{i=1}^m(y_i-w^Tx_i^*)^2=(Y-X^*w)^T(Y-X^*w) ]

这里(m)表示样本量，本例中(m=100)，(x_i,y_i)表示第(i)个样本，(X^*in R^{m imes (n+1)},Yin R^{m imes 1})，损失函数(L(w))本质上是关于(w)的函数，通过求解最小的(L(w))即可得到(w)的最优解：

[w^*=arg min_{w}L(w) ]

方法一：直接求闭式解

而对(min L(w))的求解很明显是一个凸问题（海瑟矩阵({X^*}^TX^*)正定），我们可以直接通过求解(frac{dL}{dw}=0)得到(w^*)，梯度推导如下：

[frac{dL}{dw}=-2sum_{i=1}^m(y_i-w^Tx_i^*)x_i^*=-2{X^*}^T(Y-X^*w)\ ]

令(frac{dL}{dw}=0)，可得：(w^*=({X^*}^TX^*)^{-1}{X^*}^TY)，实际情景中数据不一定能满足({X^*}^TX)是满秩（比如(m<n)的情况下，(w)的解有无数种），所以没法直接求逆，我们可以考虑用如下的方式求解：

[{X^*}^+=lim_{alpha ightarrow0}({X^*}^TX^*+alpha I)^{-1}{X^*}^T ]

上面的公式即是Moore-Penrose伪逆的定义，但实际求解更多是通过SVD的方式：

[{X^*}^+=VD^+U^T ]

其中，(U,D,V)是矩阵(X^*)做奇异值分解（SVD）后得到的矩阵，对角矩阵(D)的伪逆(D^+)由其非零元素取倒数之后再转置得到，通过伪逆求解到的结果有如下优点：

（1）当(w)有解时，(w^*={X^*}^+Y)是所有解中欧几里得距离(||w||_2)最小的一个；

（2）当(w)无解时，通过伪逆得到的(w^*)是使得(X^*w^*)与(Y)的欧几里得距离(||X^*w^*-Y||_2)最小

方法二：梯度下降求解

但对于数据量很大的情况，求闭式解的方式会让内存很吃力，我们可以通过随机梯度下降法（SGD）对(w)进行更新，首先随机初始化(w)，然后使用如下的迭代公式对(w)进行迭代更新：

[w:=w-etafrac{dL}{dw} ]

三.模型训练

目前我们推导出了(w)的更新公式，接下来编码训练过程：

#参数初始化
w=np.random.random(size=(2,1))
#更新参数
epoches=100
eta=0.0000001
losses=[]#记录loss变化
for _ in range(epoches):
    dw=-2*X.T.dot(Y-X.dot(w))
    w=w-eta*dw
    losses.append((Y-X.dot(w)).T.dot(Y-X.dot(w)).reshape(-1))
w

array([[3.01687627],
       [0.0649504 ]])

#可视化
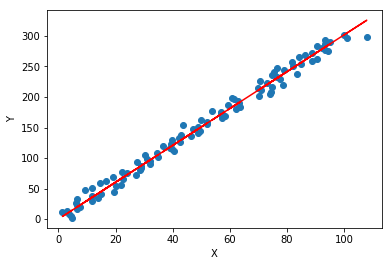
plt.scatter(X[:,0],Y)
plt.plot(X[:,0],X.dot(w),'r')
plt.xlabel('X')
plt.ylabel('Y')

Text(0,0.5,'Y')

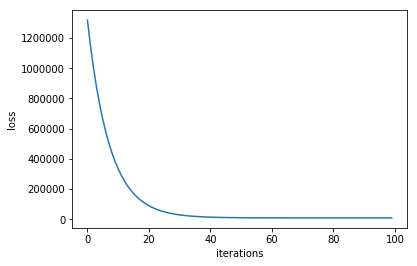
#loss变化
plt.plot(losses)
plt.xlabel('iterations')
plt.ylabel('loss')

Text(0,0.5,'loss')

#当然也可以直接求显式解
w=np.linalg.pinv(X).dot(Y)
w

array([[2.97642542],
       [2.9148446 ]])

#可视化
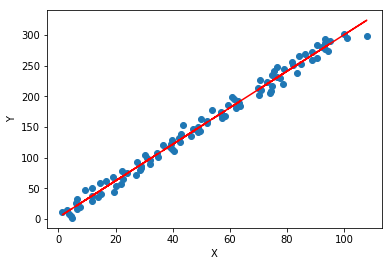
plt.scatter(X[:,0],Y)
plt.plot(X[:,0],X.dot(w),'r')
plt.xlabel('X')
plt.ylabel('Y')

Text(0,0.5,'Y')

四.问题讨论

在上面的梯度下降的例子中存在一个问题，(w_1)基本能收敛到3附近，而(w_2)却基本在0附近，很难收敛到2，说明(w_1)比(w_2)更容易收敛((w=[w_1,w_2]^T))，这很容易理解，模型可以写作：(f(x)=x*w_1+1cdot w_2)，如果(x)量纲比1大很多，为了使(f(x))变化，只需更新少量的(w_1)就能达到目的，而(w_2)的更新动力略显不足；可以考虑用如下方式：

（1）对输入(X)进行归一化，使得(x)无量纲，(w_1,w_2)的更新动力一样（后面封装代码时添加上），如下图；

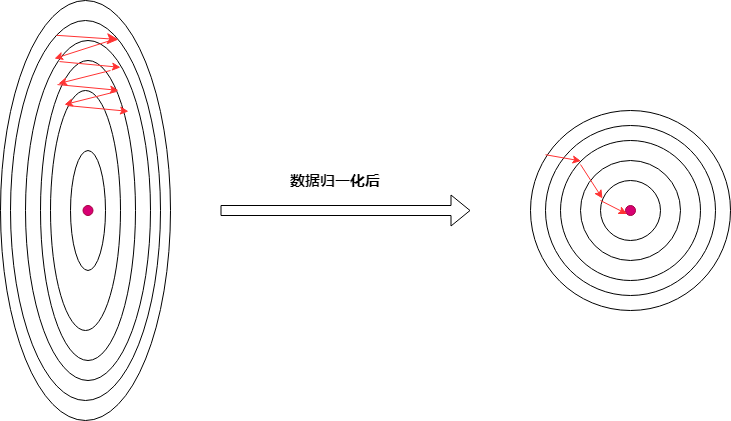
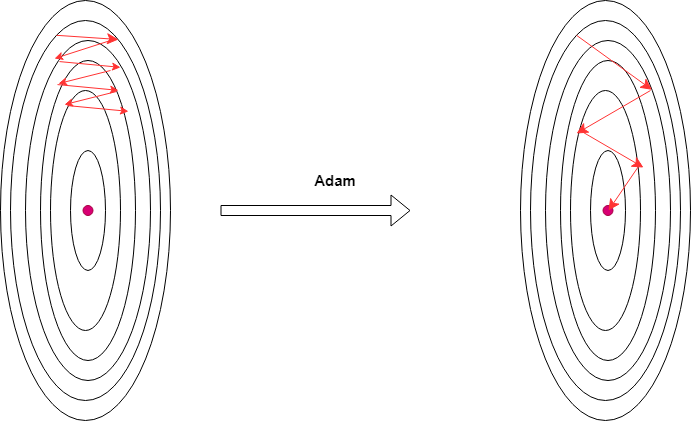
（2）梯度更新时，(w_1,w_2)使用了一样的学习率，可以让(w_1,w_2)使用不一样的学习率进行更新，比如对(w_2)使用更大的学习率进行更新（可以利用学习率自适应一类的梯度下降法，比如adam），如下图：

五.封装与测试

接下来简单封装线性回归模型，并放到ml_models.linear_model模块便于后续使用；

class LinearRegression(object):
    def __init__(self, fit_intercept=True, solver='sgd', if_standard=True, epochs=10, eta=1e-2, batch_size=1):
        """
        :param fit_intercept: 是否训练bias
        :param solver:
        :param if_standard:
        """
        self.w = None
        self.fit_intercept = fit_intercept
        self.solver = solver
        self.if_standard = if_standard
        if if_standard:
            self.feature_mean = None
            self.feature_std = None
        self.epochs = epochs
        self.eta = eta
        self.batch_size = batch_size

    def init_params(self, n_features):
        """
        初始化参数
        :return:
        """
        self.w = np.random.random(size=(n_features, 1))

    def _fit_closed_form_solution(self, x, y):
        """
        直接求闭式解
        :param x:
        :param y:
        :return:
        """
        self.w = np.linalg.pinv(x).dot(y)

    def _fit_sgd(self, x, y):
        """
        随机梯度下降求解
        :param x:
        :param y:
        :param epochs:
        :param eta:
        :param batch_size:
        :return:
        """
        x_y = np.c_[x, y]
        # 按batch_size更新w,b
        for _ in range(self.epochs):
            np.random.shuffle(x_y)
            for index in range(x_y.shape[0] // self.batch_size):
                batch_x_y = x_y[self.batch_size * index:self.batch_size * (index + 1)]
                batch_x = batch_x_y[:, :-1]
                batch_y = batch_x_y[:, -1:]

                dw = -2 * batch_x.T.dot(batch_y - batch_x.dot(self.w)) / self.batch_size
                self.w = self.w - self.eta * dw

    def fit(self, x, y):
        # 是否归一化feature
        if self.if_standard:
            self.feature_mean = np.mean(x, axis=0)
            self.feature_std = np.std(x, axis=0) + 1e-8
            x = (x - self.feature_mean) / self.feature_std
        # 是否训练bias
        if self.fit_intercept:
            x = np.c_[x, np.ones_like(y)]
        # 初始化参数
        self.init_params(x.shape[1])
        # 训练模型
        if self.solver == 'closed_form':
            self._fit_closed_form_solution(x, y)
        elif self.solver == 'sgd':
            self._fit_sgd(x, y)

    def get_params(self):
        """
        输出原始的系数
        :return: w,b
        """
        if self.fit_intercept:
            w = self.w[:-1]
            b = self.w[-1]
        else:
            w = self.w
            b = 0
        if self.if_standard:
            w = w / self.feature_std.reshape(-1, 1)
            b = b - w.T.dot(self.feature_mean.reshape(-1, 1))
        return w.reshape(-1), b

    def predict(self, x):
        """
        :param x:ndarray格式数据: m x n
        :return: m x 1
        """
        if self.if_standard:
            x = (x - self.feature_mean) / self.feature_std
        if self.fit_intercept:
            x = np.c_[x, np.ones(shape=x.shape[0])]
        return x.dot(self.w)

    def plot_fit_boundary(self, x, y):
        """
        绘制拟合结果
        :param x:
        :param y:
        :return:
        """
        plt.scatter(x[:, 0], y)
        plt.plot(x[:, 0], self.predict(x), 'r')

#测试
lr=LinearRegression(solver='sgd')
lr.fit(X[:,:-1],Y)
predict=lr.predict(X[:,:-1])
#查看w
print('w',lr.get_params())
#查看标准差
np.std(Y-predict)

w (array([2.97494802]), array([[3.14004069]]))





9.198087733141367

#可视化结果
lr.plot_fit_boundary(X[:,:-1],Y)

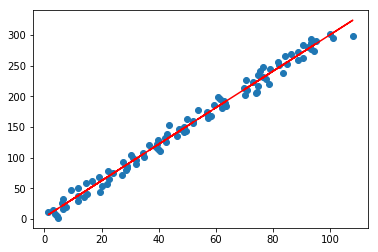
#测试
lr=LinearRegression(solver='closed_form')
lr.fit(X[:,:-1],Y)
predict=lr.predict(X[:,:-1])
#查看w
print('w',lr.get_params())
#查看标准差
np.std(Y-predict)

w (array([2.97642542]), array([[2.9148446]]))





9.197986388759377

#可视化结果
lr.plot_fit_boundary(X[:,:-1],Y)

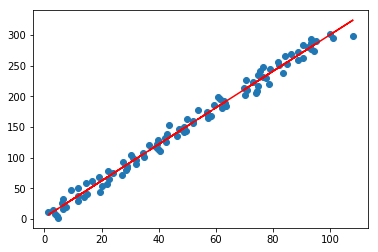
#与sklearn对比
from sklearn.linear_model import LinearRegression
lr=LinearRegression()
lr.fit(X[:,:-1],Y)
predict=lr.predict(X[:,:-1])
#查看w,b
print('w:',lr.coef_,'b:',lr.intercept_)
#查看标准差
np.std(Y-predict)

w: [[2.97642542]] b: [2.9148446]





9.197986388759379