数组:
1、给定一个数组和一个值,删除该值的所有实例并返回新的长度。 元素的顺序可以改变。 你留下的新长度并不重要
这道题很坑爹,是牛客网里的一道题,也不知道是我的理解能力差,还是它的英文写的有问题,它的测试案例很偏,不得不像下面这么做。
class Solution { public: int removeElement(int A[], int n, int elem) { if (n == 0) return n; for (int i = 0; i < n; ++i){ if (A[i] == elem) { while (n>i && A[--n] == elem); A[i] = A[n]; } } return n; } };
2、给定排序数组,删除重复项,使每个元素只出现一次并返回新长度。
不要为另一个数组分配额外的空间,必须使用常量内存来执行此操作。
例如,
给定输入数组A = [1,1,2],
你的函数应该返回length = 2,A现在是[1,2]
class Solution { public: int removeDuplicates(int A[], int n) { if(n==0) return n; int i=0; // 慢指针 for(int j=1;j<n;j++) //快指针 { if(A[i]!=A[j]) //如果快慢两指针指向地址内的值相同,则跳过 { //若不相同,则将快指针指向的值放在慢指针的后面 A[++i] = A[j]; } } return ++i; // 数组的长度 } };
3、您将获得表示图像的n x n 2D矩阵。
将图像旋转90度(顺时针)。
跟进:
你能这样做吗?
思路:其实这道题就是将数组顺时针旋转90°
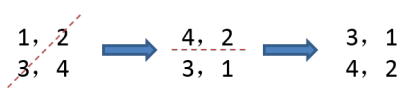
按照图像需要做两部翻转,第一步是对角线翻转,第二部是上下翻转
class Solution { public: void rotate(vector<vector<int> > &matrix) { int row = (int)matrix.size(); int col = (int)matrix[0].size(); int a = row - 1; int b = col - 1; int target = matrix[row-1][0]; //对角线翻转 for(int i=0;i<row;i++) { for(int j=0;j<col-i;j++) { int temp = matrix[i][j]; matrix[i][j] = matrix[b-j][a-i]; matrix[b-j][a-i] = temp; } } //从中间翻转 for(int i=0;i<row/2;i++) { for(int j=0;j<col;j++) { int temp = matrix[i][j]; matrix[i][j] = matrix[a-i][j]; matrix[a-i][j] = temp; } } } };
4、给定未排序的整数数组,找到第一个缺少的正整数。
例如,
鉴于[1,2,0] return3,
和[3,4,-1,1] RETURN2。
您的算法应该在O(n)时间运行并使用恒定空间。
思路:
class Solution { public: int firstMissingPositive(int A[], int n) { if(n==0) return 1; for(int i=0;i<n;i++){ //A[i] - 1 < A.length超出范围不交换,A[i] != A[A[i] - 1] 相等不交换 while(A[i]>0 && A[i]!=i+1 && A[i]-1<n && A[i]!=A[A[i]-1]){ change(A,i,A[i]-1); } } for (int i = 0; i < n; i++) { if (A[i] != i + 1) { return i + 1; // 第一个不相等就返回 } } return A[n-1]+1; // 数组交换后是有序正数,就返回最大 + 1 } void change(int A[],int i,int j) { int temp = A[i]; A[i] = A[j]; A[j] = temp; } };
5、实现下一个排列,它将数字重新排列到字典上的下一个更大的数字排列。
如果这种安排不可能,则必须将其重新排列为尽可能低的顺序(即按升序排序)。
替换必须就地,不要分配额外的内存。
这里有些例子。 输入位于左侧列中,其相应的输出位于右侧列中。
1,2,3→1,3,2
3,2,1→1,2,3
1,1,5-→1,5,1
思路:从后往前先找到不满足递增排序的点,swap这个点与后面大于此的数,然后对后面升序排列
class Solution { public: void nextPermutation(vector<int> &num) { int n = num.size(); int i = n-1; if(n==0) return; //先找到数组后面数比前面数大的下标 while(i>0 && num[i-1]>=num[i]) --i; //若下标为0,则代表该数组是降序排列,改为升序排列 if(i==0){ reverse(num.begin(),num.end()); } //若下标不为0。则代表存在一个数大于前面的数 else{ //找到数组最后的数 int j=n-1; //如果该数小于数组最后的数 while(num[j]<=num[i-1]) --j; swap(num[j],num[i-1]); reverse(num.begin()+i,num.end()); } } };
6、给定一个数字表示为数字数组,加上一个数字。
思路:这题是什么意思呢?例如有个数字为10010,将这个数字放在数组里,该数组为{1,0,0,1,0},然后再这个数组上加1,的到最后的数组,但上面的情况是非常好的情况,如果是向下面这样的数组{1,0,0,9,9},这就涉及进位了。所以该题最好是从数组的右面向左进行运算,求出它每个位的余数。
class Solution { public: vector<int> plusOne(vector<int> &digits) { int carry = 1; int n = digits.size(); for(int i=n-1;i>=0;--i){ int cur_sum = digits[i] + carry; // 当前数字 + 进位 digits[i] = cur_sum%10; carry = cur_sum/10; // 进位 } if(carry>0) digits.insert(digits.begin(),carry); return digits; } };
7、给定整数n,以螺旋顺序生成填充有1到n 2的元素的方阵。
例如,
给定n = 3,
你应该返回以下矩阵:
[
[1,2,3],
[8,9,4],
[7,6,5]
]
思路:先从外圈开始,在转到内圈,直到最后一个数
class Solution { public: vector<vector<int> > generateMatrix(int n) { vector<vector<int> > res; if (n < 1) return res; int index = 1, rowStart = 0, rowEnd = n - 1, colStart = 0, colEnd = n - 1; while (index <= n * n) { for (int i = colStart; i <= colEnd; i++) res[rowStart][i] = index++; for (int i = rowStart + 1; i <= rowEnd; i++) res[i][colEnd] = index++; for (int i = colEnd - 1; i >= colStart; i--) res[rowEnd][i] = index++; for (int i = rowEnd - 1; i > rowStart; i--) res[i][colStart] = index++; rowStart += 1; rowEnd -= 1; colStart += 1; colEnd -= 1; } return res; } };
8、给定m×n个元素的矩阵(m行,n列),以螺旋顺序返回矩阵的所有元素。
例如,
给出以下矩阵:
[
[1,2,3],
[4,5,6],
[7,8,9]
]
你应该返回[1,2,3,6,9,8,7,4,5]。
思路:该题思路和上题一样,就是不是往里面填数而是取数。
class Solution { public: vector<int> spiralOrder(vector<vector<int> > &matrix) { if(matrix.empty()) return vector<int>(); int col = matrix.size(); int row = matrix[0].size(); int left = 0,right = row-1; int top = 0,bottom = col-1; vector<int> num; while(1) { for(int i=left;i<=right;i++) num.push_back(matrix[top][i]); if(++top > bottom) break; for(int j=top;j<=bottom;j++) num.push_back(matrix[j][right]); if(--right < left) break; for(int i=right;i>=left;i--) num.push_back(matrix[bottom][i]); if(--bottom < top) break; for(int j=bottom;j>=top;j--) num.push_back(matrix[j][left]); if(++left > right) break; } return num; } };
9、跟进“删除重复项”:
如果重复最多允许两次怎么办?
例如,
给定排序数组A = [1,1,1,2,2,3],
你的函数应该返回length = 5,A现在是[1,1,2,2,3]。
class Solution { public: int removeDuplicates(int A[], int n) { if(n<2) return n; int index = 2; for(int i=2;i<n;i++){ if(A[i]!=A[index-2]) //不等则计数,相等则跳过不计数 A[index++]=A[i]; } return index; } };
10、给定一个具有红色,白色或蓝色的n个对象的数组,对它们进行排序,使相同颜色的对象相邻,颜色顺序为红色,白色和蓝色。
这里,我们将使用整数0,1和2分别表示红色,白色和蓝色。
注意:
您不应该使用库的排序功能来解决此问题。
点击显示跟进。
跟进:
一个相当直接的解决方案是使用计数排序的两遍算法。
首先,迭代0,1,和2的数组计数,然后覆盖总数为0的数组,然后是1,然后是2。
你能想出一个只使用恒定空间的一次通过算法吗?
class Solution { public: void sortColors(int A[], int n) { int left = 0; int right = n-1; int i=0; while(i < right+1) { if(A[i]==0) { swap(A[i],A[left]); left++; i++; }else if(A[i]==2){ swap(A[i],A[right]); right--; }else{ i++; } } } };
11、编写一个有效的算法,搜索m×n矩阵中的值。 该矩阵具有以下属性:
每行中的整数从左到右排序。
每行的第一个整数大于前一行的最后一个整数。
例如,
考虑以下矩阵:
[
[1,3,5,7],
[10,11,16,20],
[23,30,34,50]
]
class Solution { public: bool searchMatrix(vector<vector<int> > &matrix, int target) { int row = matrix.size(); int col = matrix[0].size(); vector<int> num; bool result=false; //将matrix数组里的树全部放入到容器num里 for(int i=0;i<row;i++) for(int j=0;j<col;j++) num.push_back(matrix[i][j]); int n = num.size(); //判断容器num里是否存在该数 for(int i=0;i<n;i++) if(num[i]==target) result = true; return result; } };
12、给定包含'X'和'O'的2D板,捕获由'X'包围的所有区域。
通过将所有'O'翻转到该周围区域中的'X'来捕获区域。
例如,
X X X X.
X O O X.
X X O X.
X O X X.
运行功能后,主板应该是:
X X X X.
X X X X.
X X X X.
X O X X.
所有与四条边相连的O都保留,其他O都变为X遍历四条边上的O,并深度遍历与其相连的O,将这些O都转为*将剩余的O变为X将剩余的*变为Oclass Solution { public: int rowNum = 0; int colNum = 0; void solve(vector<vector<char> > &board) { rowNum = board.size(); colNum = board[0].size(); for(int i = 0; i < colNum; i++){ dfs(board, 0, i); dfs(board, rowNum-1, i); } for(int i = 0; i < rowNum; i++){ dfs(board, i, 0); dfs(board, i, colNum-1); } for(int i = 0; i < rowNum; i++){ for(int j = 0; j < colNum; j++){ if(board[i][j] == 'O'){ board[i][j] = 'X'; } } } for(int i = 0; i < rowNum; i++){ for(int j = 0; j < colNum; j++){ if(board[i][j] == '*'){ board[i][j] = 'O'; } } } } void dfs(vector<vector<char> > &board, int row, int col) { // TODO Auto-generated method stub if(board[row][col] == 'O'){ board[row][col] = '*'; if(row > 1){ dfs(board, row-1, col); } if(col > 1){ dfs(board, row, col-1); } if(row < rowNum-1){ dfs(board, row+1, col); } if(col < colNum-1){ dfs(board, row, col+1); } } } };
13、给定两个排序的整数数组A和B,将B合并为A作为一个排序的数组。
注意:
您可以假设A有足够的空间来容纳B中的其他元素.A和B中初始化的元素数分别为m和n。
i从A的末尾,j从B末尾开始,两两比较,大的放在末端。比如A[4,5,7] B[1,2,6],。7比6大,A[5]处放置7,然后i前移。再次比较5 和6,6放在A[4]处。如此类推如果A穷尽,把B元素依次放进A的前几个位置,如果B穷尽,正好结束。class Solution { public: void merge(int A[], int m, int B[], int n) { int aindex = m-1; int bindex = n-1; int counts = m+n-1; while(aindex>=0 && bindex>=0) A[counts--] = A[aindex] > B[bindex] ? A[aindex--] : B[bindex--]; while(bindex>=0) A[counts--] = B[bindex--]; } };
14、假设您有一个数组,其中第i个元素是第i天给定股票的价格。
设计算法以找到最大利润。 您最多可以完成两笔交易。
注意:
您不得同时进行多笔交易(即,您必须在再次购买之前卖出股票)。
class Solution { public: int maxProfit(vector<int> &prices) { int buy1 = INT_MIN, sell1 = 0, buy2 = INT_MIN, sell2 = 0; for(auto u:prices) { //每次循环表示进入新的一天 buy1 = max(buy1,-u); //记录之前所有天最便宜的股价 sell1 = max(sell1,buy1 + u); //记录之前所有天只进行1次买卖的最大利益 buy2 = max(buy2,sell1 - u); //记录之前天先进行1次交易获得最大利益后, //再买到那次交易后最便宜股价时剩余的净利润 sell2 = max(sell2,buy2 + u); //记录之前天进行2次完整交易的最大利润 } return sell2; } };
思路:
如此循环下去,到最后一天结束,sell1就记录了一次交易的最大利润。
进行2次交易的道理是可以类推的。
class Solution { public: int maxProfit(vector<int> &prices) { int buy1 = INT_MIN, sell1 = 0, buy2 = INT_MIN, sell2 = 0; for(auto u:prices) { //每次循环表示进入新的一天 buy1 = max(buy1,-u); //记录之前所有天最便宜的股价 sell1 = max(sell1,buy1 + u); //记录之前所有天只进行1次买卖的最大利益 buy2 = max(buy2,sell1 - u); //记录之前天先进行1次交易获得最大利益后, //再买到那次交易后最便宜股价时剩余的净利润 sell2 = max(sell2,buy2 + u); //记录之前天进行2次完整交易的最大利润 } return sell2; } };
15、假设您有一个数组,其中第i个元素是第i天给定股票的价格。
设计算法以找到最大利润。 您可以根据需要完成尽可能多的交易(即,多次买入并卖出一股股票)。 但是,您可能不会同时进行多笔交易(即,您必须在再次购买之前卖出股票)。
思路如下:
本题由于允许多次交易(每次必须先卖出再买进),所以不好用爆搜
分析可知,要想利益最大化,就应该每次在波谷买进,波峰卖出,这样利益最大,操作次数最少
应该是使用动态规划来做可能比较简洁,个人觉得。
class Solution { public: int maxProfit(vector<int> &prices) { int len = prices.size(); vector<int> num(len,0); int maxpro=0; for(int i=1;i<len;i++){ //记录所有长和跌的情况 num[i] = prices[i]-prices[i-1]; //累加所有长幅,即为最大收益 if(num[i]>0) maxpro+=num[i]; } return maxpro; } };
16、假设您有一个数组,其中第i个元素是第i天给定股票的价格。
如果您只被允许完成最多一笔交易(即买入并卖出一股股票),请设计一个算法来查找最大利润。
从左往右遍历向量,遇到当前最小值,则保存,如果不是最小值,则计算它到最小值的距离,保存为最大利润class Solution { public: int maxProfit(vector<int> &prices) { int n = prices.size(); int max_price=0; int min_price=prices[0]; for(int i=0;i<n;i++){ if(prices[i]<min_price) min_price = prices[i]; if((prices[i]-min_price)>max_price) max_price = prices[i]-min_price; } return max_price; } };
17、给定未排序的整数数组,找到最长连续元素序列的长度。
例如,
鉴于[100,4,2,1,3,2],
最长的连续元素序列是[1,2,3,4]。 返回长度:4。
您的算法应该以O(n)复杂度运行。
class Solution { public: int longestConsecutive(vector<int> &num) { sort(num.begin(),num.end()); int n = num.size(); if(n==0 || n== 1) return n; unique(num.begin(),num.end()); int result=0,cnt=1; for(int i=0;i<n-1;i++){ if(num[i]+1!=num[i+1]){ result = result>cnt ? result : cnt; cnt=0; } cnt++; } return result = result>cnt ? result : cnt; } };