这是T1,但是是神仙T1:

对于前100%的数据很好写,直接数组模拟就可以了:
(当然也有栈模拟的,据说有模拟炸了的)
//50pts
#include<bits/stdc++.h> using namespace std; inline int read() { int ans=0; char last=' ',ch=getchar(); while(ch>'9'||ch<'0') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') ans=(ans<<1)+(ans<<3)+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } char Getchar() { char ch=' '; do { ch=getchar(); } while(ch==' '||ch==' '||ch=='�'||ch==' '||ch==' '); return ch; } int n,num; char ops; char s[1000010]; int main() { n=read(); int zz=1; for(int i=1; i<=n; i++) { ops=Getchar(); if(ops=='T') { s[zz]=Getchar(); zz++; } if(ops=='Q') { num=read(); printf("%c ",s[num]); } if(ops=='U') { num=read(); zz-=num; } } return 0; }
然后真的要安利的一点:手写读入char字符Getchar;
从water_lift姐姐那偷师学来的,然后真的好用,可以过滤多余的空格回车换行制表符……
这样与读入的斗争就会简单了呢qwq;
然后来看100pts思路;
我们可以建立n个栈(用数组模拟),
每一个栈储存第n次操作(应该是不算查询的)后序列的样子
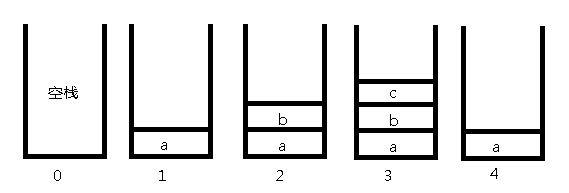
看样例:
7
T a
T b
T c
Q 2
U 2
T c
Q 2
T 2:

现在有2个栈,一个为空栈,一个为插入了一个元素a后的栈;
T b:

将栈1先复制给栈2,然后在栈2中插入一个b;
T c:

同理,现在共有四个栈;
Q 2:
直接用数组下标查询最后一个栈中的元素(因为我们用数组模拟的栈),可以做到O(1)查询;
U 2:
需要撤销两步,咋的办呢?我们就将当前操作的序号(为4)(不算查询)减1再减2(也就是需要撤销的步数),然后将其的栈拷贝过来(这样就可以应对撤销撤销撤销了):
然后这个思路,除了空间会爆,没有什么缺点
但是我们可以对这个思路进行优化:
试想一下,当n越大,栈中需要拷贝的数,可能增多,尤其是当出现撤销插入撤销插入的毒瘤数据时,你剩下的几百个元素吧,都没有用到,但是你每次都需要把它拷贝一遍,明显是即占空间又占时间的;
因此我们可以考虑链表维护:
对于每一个链表当中的结点,我们维护两个数据,第一个是这个结点的字母,第二个是这个结点上一个结点是哪一个:
这样当插入时,我们只需要新建一个结点将新插入的字符写到字母数据中,将nxt指向上一个结点就可以了;
当需要撤销时,同样新建一个结点,并且将这个结点拷贝成(当前操作数-1-撤销步数)这个结点的信息(表示撤销了撤销步数步操作),下次再添加时,直接在当前结点的基础上加就好了;
考虑一下复杂度,我们可以做到O(1)插入,O(1)撤销,但是查询却需要O(n),这也不够优秀,我们还需改进;
考虑分块来做,我们设置一个最长长度B(动态维护B为√n),对于插入和撤销,还是像上面一样,只是当插入的时候,我们判断当前这个块有没有满,若没满,直接在后面插入,否则,新建一个块,再插入。
然后对于查询,我们知道了x和一个块的大小B,我们可以先跳过x/B(整除好评qwq)个块,然后再从x所在的块里面寻找x。因为我们模拟链表只能从后往前找,所以实际上我们需要算的是 总的元素个数-x+1;
对于这套思路,还是可以理解的,但是作为noip选手,到现在都(jiao)没(lian)有(bu)学(rang)指针,因此除了代码实现,莫得什么问题了呢qwq;
nili water_lift姐姐的代码:
#include <cmath> #include <cstdio> #include <cstring> template <class T> inline void read(T &num) { bool flag = 0; num = 0; char c = getchar(); while ((c < '0' || c > '9') && c != '-') c = getchar(); if (c == '-') { flag = 1; c = getchar(); } num = c - '0'; c = getchar(); while (c >= '0' && c <= '9') num = (num << 3) + (num << 1) + c - '0', c = getchar(); if (flag) num *= -1; } inline void read(char &c) { do { c = getchar(); } while (c == ' ' || c == ' ' || c == ' '); } template <class T> inline void output(T num) { if (num < 0) { putchar('-'); num = -num; } if (num >= 10) output(num / 10); putchar(num % 10 + '0'); } template <class T> inline void outln(T num) { output(num); putchar(' '); } template <class T> inline void outps(T num) { output(num); putchar(' '); } template <class T> inline T max(T a, T b) { return a < b ? b : a; } const int N = 100000; int n, B; struct node { char *s; int now, pc; node *pre; node() { now = pc = 0; s = new char[B]; pre = NULL; } void copy(node *src) { now = src->now; pc = src->pc; pre = src->pre; for (int i = 0; i < now; i++) { s[i] = src->s[i]; } } } * head[N]; int lst; void append(char x) { if (head[lst]->now == B) { head[++lst] = new node; head[lst]->pre = head[lst - 1]; head[lst]->pc = head[lst - 1]->pc + 1; head[lst]->s[head[lst]->now++] = x; } else { head[++lst] = new node; head[lst]->copy(head[lst - 1]); head[lst]->s[head[lst]->now++] = x; } } char query(int x) { int siz = head[lst]->now + head[lst]->pc * B; x = siz - x + 1; if (x <= head[lst]->now) { return head[lst]->s[head[lst]->now - x]; } x -= head[lst]->now; node *now = head[lst]->pre; while (x > B) { now = now->pre; x -= B; } return now->s[B - x]; } int main() { read(n); B = sqrt(n); head[0] = new node; for (int i = 1; i <= n; i++) { char op; read(op); if (op == 'T') { char x; read(x); append(x); } if (op == 'U') { int x; read(x); head[lst + 1] = head[lst - x]; lst += 1; } if (op == 'Q') { int x; read(x); putchar(query(x)); putchar(' '); } } }
end-