此题在luogu上模数是2015,考试题的模数是2012。
然后这道题听说好多人是打表找规律的(就像7.9T2一样)(手动滑稽_gc)
另外手动

sy,每次测试都无意之间bibi正解,然后说自己是不会做是个什么骚气操作。
所以我们来看真.题解;
SOLUTION:
首先,输入莫得什么好说的;
当然想用快读咱也拦不住(就是想用咬我啊);
咱可能最近因为学长讲了一道DP,印象比较深刻,所以咱居然看到这道题就想到正解应该是DP了!?
接下来就是设计DP状态了:
dp[i][j]表示i个数,恰有j个‘<’的排列方案数;
转移就很神奇很有意思了:
当我们已知dp[1~i-1][1~k]时,我们考虑求dp[i][j];
当数从i-1~i时,显然数列增加的数是大于1~i-1的(莫得因为什么,不好解释,感性理解);我们考虑把i这个数加在哪里:
①加在序列的最左侧:
因为i>1~i-1的任何一个数,所以一定是‘>’,因此对‘<’的多少没有影响;
②加在序列最右侧:
同理因为i>1~i-1任何一个数,所以当将i放在序列最右侧时,一定会增加一个‘<’;
③加在一个‘<’的中间:
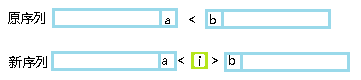
实际上不会增加‘<’,因此不会对答案产生影响qwq;
④加在一个‘>’中间:
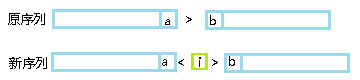
增加了一只‘<’。
所以由此我们可以推出状态转移方程:
当i加在第①③种情况时,不会产生新的‘<’,因此我们需要由dp[i-1][j]推过来。
可以计算1~i-1的序列中,共有j个‘<’号,然后还有①情况中的一种,共有j+1种情况是添加后不增加‘<’的,所以dp[i][j]+=dp[i-1][j]*(j+1);
当i加在第②④种情况时,会产生新的'<',因此我们也需要由dp[i-1][j-1]推得:
④情况:我们知道当前情况下1~i-1中共有j-1个‘>’,总共的符号数为i-2个,因此其中‘>’数为i-2-(j-1)=i-j-1个,再加上②情况的一种,所以共有i-j个可以产生一个新的‘<’;因此dp[i][j]+=dp[i-1][j-1]*(i-j);
转移方程:dp[i][j]=dp[i-1][j]*(j+1)+dp[i-1][j-1]*(i-j);//注意取模
然后是初始状态:
当我们有0个‘<’时,无论有几个数,这些数必须严格升序排列,也就是只有一种排列是满足有0个‘<’的;因此初始化:dp[1~n][0]=1;
最后的答案显然就是dp[n][k]了;
CODE:
#include<bits/stdc++.h> using namespace std; int n,k; int dp[1010][1010]; int main(){ scanf("%d %d",&n,&k); for(int i=1;i<=n;i++) dp[i][0]=1; for(int i=1;i<=n;i++){ for(int j=1;j<=k;j++){ dp[i][j]=(dp[i-1][j]*(j+1)%2015+dp[i-1][j-1]*(i-j)%2015)%2015; } } printf("%d",dp[n][k]); return 0; }
end-