这些东西大部分之前都学过了啊qwq
zhx大概也知道我们之前跟着他学过这些了qwq,所以:
先讲新的东西qwq:(意思就是先讲我们没有学过的东西)
进制转换
10=23+21=1010(2)
=32+30=101(3)
进制转换的两种操作:
1.10进制=>k进制
短除法:

55(10):
55/3=18……1
18/3=6…… 0
6/3=2…… 0
2/3=0…… 2
55(10)=2001(3)
2.k进制=>10进制
k进制数x,n~0
xnxn-1xn-2……x0(k)
= xn*kn+xn-1*kn-1+xn-2*kn-2……x0*k0
特殊的进制:
二进制 想要的二进制表示前+0 举个栗子:01001 c++识别为9
八进制
十进制
十六进制 想要直接写16进制数+0x 举个栗子:0x1001=16 3+160=4097;10~15:用字母代表 A=10,B=11,C=12……F=15
0x3f3f3f3f= 3*167+15*166+3*165+15*164+3*163+15*162+3*161+15*160

高精度:
int -231~231-1
long long -263~263-1≈1020
目的:解决大数运算
方法:竖式加减乘除法
加法:个位对齐,逐位相加。
2333+233=2566 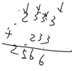
储存:
19260817
从0~n,存从最高位到最低位✘ 对不齐(麻烦)

0=>n 存 个位=>最高位

这时个位一定对齐的,逐位相加就可以了qwq
乘法:
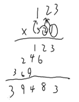
回到数论qwq:
质数:

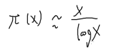
素数判定:O(根号n)
证明啊qwq:
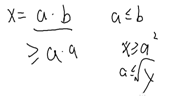

筛法:
#include<iostream>
for(int i=2;i<=n;i++)
for(int b=i*2;b<=n;b+=i)
not_prime[b]=true;
约等于=n(1+1/2+1/3+……+1/n);调和级数
约等于nlogn
埃氏筛:
O(nloglogn)
一个合数,一定会被筛质数的倍数是被筛掉
for(int i=2;i<=n;i++)
if(not_prime[i] =false) //只筛掉质数的倍数
for(int b=i*2;b<=n;b+=i)
not_prime[b]=true;
线性筛:(保证每个数只被最小的质因数筛掉)
memset(not_prime,0,sizeof(not_prime));
not_prime[1]=true;
for(int i=2;i<=n;i++){}
if(!not_prime[i])prime[++prime_count]=i;
for(int j=1;j<=prime_count;j++){
if(prime[j]*i>n)break;
not_prime[prime[j]*i]=true;
if(i%prime[j]==0)break;//保证每个数只被筛一次且是被他最小质因子筛掉;
}
}
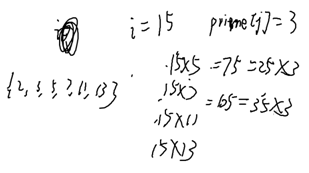
gcd:
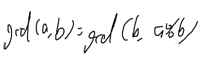
int gcd(int a,int b){
if(b==0) return a;
else return gcd(b,a%b);
}
内置函数:__gcd(下划线下划线gcd)(最好不要用)
扩展欧几里得算法qwq
令gcd(a,b)=g;
那么ax+by=g;
现在已知gcd(a,b)=g;
求得ax+by=g的一组解;
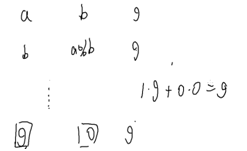


逆元:
费马小:
 (mod p)
(mod p)

欧拉定理:
 (mod m)
(mod m)
gcd(a,m)=1;
φ(m),有几个数和m是互质的:
m分解质因数: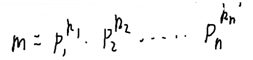
φ(m)= 
费马小是欧拉的特殊形式qwq
mod m,m不是质数;
/x <=> *xφ(m)-1(mod m)
end-