简单数据结构
入门题:
在初学OI的时候,总会遇到这么一道题。
给出N次操作,每次加入一个数,或者询问当前所有数的最大值。
维护一个最大值Max,每次加入和最大值进行比较。
时间复杂度O(N).
给出N次操作,每次加入一个数,删除一个之前加入过的
数,或者询问当前所有数的最大值。
N ≤ 100000
二叉搜索树(BST)是用有根二叉树来存储的一种数据结构,在二叉树中每个节点代表一个数据。
每个节点包含一个指向父亲的指针,和两个指向儿子的指针。如果没有则为空。
每个节点还包含一个key值,代表他本身这个点的权值。
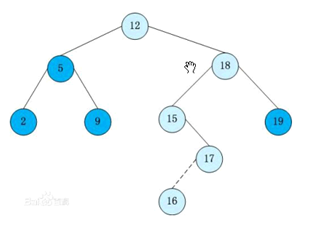
二叉搜索树的key值是决定树形态的标准。
每个点的左子树中,节点的key值都小于这个点。
每个点的右子树中,节点的key值都大于这个点
在接下来的介绍中,我们将以ls[x]表示x的左儿子,rs[x]表示x的右儿子,fa[x]表示x的父亲,key[x]表示x这个点的权值。
基本操作:
插入一个数,删除一个数,询问最大/最小值,询问第k大值。
当然,在所有操作结束后,它还能把剩下的数从小到大输出来。
查询最大/最小值:
注意到BST左边的值都比右边小,所以如果一个点有左儿子,就往左儿子走,否则这个点就是最小值啦。

插入一个值:(左侧的数要比它的父亲小,右边的要比它的父亲大)
现在我们要插入一个权值为x的节点。
为了方便,我们插入的方式要能不改变之前整棵树的形态。
首先找到根,比较一下key[root]和x,如果key[root] < x,节点应该插在root右侧,否则在左侧。
看看root有没有右儿子,如果没有,那么直接把root的右儿子赋成x就完事了。
否则,为了不改变树的形态,我们要去右儿子所在的子树里继续这一操作,直到可以插入为止。
3 1 5 4 2


删除一个值:
删除一个权值为x的点:
- 定位一个节点。要删除首先要知道这个点在哪里
从root开始,想插入一样(判断向左走还是向右走)找某个树
删除:
方案1:
直接把结点赋成空的状态(不易查询)
方案2:
对这个结点x的儿子进行考虑,若x没有结点,直接删掉。
如果x有1个儿子,直接把x的儿子接到x的父亲下面就行
如果x有两个儿子:
先在右侧找权值最小的点y
把y的子孙连接到y的父亲上
用y替换x
定义x的后继(没有左儿子)y,是x右子树中所有点里,权值最小的点。
找这个点可以x先走一次右儿子,再不停走左儿子。
如果y是x的右儿子,那么直接把y的左儿子赋成原来x的左儿子,然后用y代替x的位置。
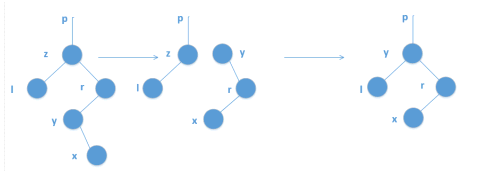
一个绝妙的实现方法:
#include<cstdio> #include<algorithm> #include<cstring> #include<iostream> #include<cstring> #include<string> #include<cmath> #include<ctime> #include<set> #include<vector> #include<map> #include<queue> #define N 300005 #define M 8000005 #define mid ((l+r)>>1) #define mk make_pair #define pb push_back #define fi first #define se second using namespace std; int i,j,m,n,p,k,ls[N],rs[N],sum[N],size[N],a[N],root,tot,fa[N]; void ins(int x)//插入一个权值为x的数字 { sum[++tot]=x;//用tot来表示二叉树里的节点个数 size[tot]=1; if (!root) root=tot;//没有节点 else{ int now=root; //从根开始 for (;;){ ++size[now]; if (sum[now]>sum[tot]){ //判断和当前节点的大小 if (!ls[now]){ //ls[i]存的是i的左儿子 //如果没有左儿子,就把新加入的点放在左儿子的位置 ls[now]=tot; fa[tot]=now; break; } else now=ls[now];//否则的话把当前节点置为它的左儿子,再继续比较 } else{ if (!rs[now]){ rs[now]=tot; fa[tot]=now; break; } else now=rs[now]; } } } } int FindMin()//最小值显然在左侧 { int now=root;//从树根开始比较 while (ls[now]) now=ls[now];//如果有左儿子,把当前节点置为左儿子的位置,继续寻找 return sum[now];//sum好像是存的权值 } void build1()//暴力build的方法,每次插入一个值 { for (i=1;i<=n;++i) ins(a[i]); } int Divide(int l,int r) { if (l>r) return 0; ls[mid]=Divide(l,mid-1); rs[mid]=Divide(mid+1,r); fa[ls[mid]]=fa[rs[mid]]=mid; fa[0]=0; sum[mid]=a[mid]; size[mid]=size[ls[mid]]+size[rs[mid]]+1; return mid; } void build2()//精巧的构造,使得树高是log N的 { sort(a+1,a+n+1); root=Divide(1,n); tot=n; } int Find(int x)//查询值为x的数的节点编号 { int now=root; while (sum[now]!=x&&now) if (sum[now]<x) now=rs[now]; else now=ls[now]; return now; } int Findkth(int now,int k)//递归似的寻找 { if (size[rs[now]]>=k) return Findkth(rs[now],k);//第k大的值在右边 else if (size[rs[now]]+1==k) return sum[now];//当前点是第k大的值 else Findkth(ls[now],k-size[rs[now]]-1);//第k大的值在左边 //注意到递归下去之后右侧的部分都比它要大 } void del(int x)//删除一个值为x的点 { int id=Find(x),t=fa[id];//找到这个点的编号 if (!ls[id]&&!rs[id]) //如果这个点没有左儿子也没有右儿子 { if (ls[t]==id) ls[t]=0; else rs[t]=0; //去掉儿子边 for (i=id;i;i=fa[i]) size[i]--; //长度-1; } else if (!ls[id]||!rs[id])//如果这个点没有左儿子或没有右儿子 { int child=ls[id]+rs[id];//找存在的儿子的编号 (显然没有的那个儿子编号为0) if (ls[t]==id) ls[t]=child; else rs[t]=child;//如果这个点是他父亲的左儿子,把它的儿子放到它的位置,否则放右儿子 fa[child]=t;//这个点的儿子的父亲变成了这个点原来的父亲 for (i=id;i;i=fa[i]) size[i]--;//id以上的点的长度-- } else//如果既有左儿子又有右儿子 { int y=rs[id];//先找到id的右儿子 while (ls[y]) y=ls[y]; //如果id的右儿子有左儿子,那么就更新y为左儿子 //目的是找到最小的右儿子 if (rs[id]==y) //如果id右儿子就是右侧最小的点 (这是y是id的右儿子啊) { if (ls[t]==id) ls[t]=y; //如果id是父亲的左儿子,把左儿子变成y else rs[t]=y;//否则,右儿子变为y fa[y]=t; ls[y]=ls[id];//y的左儿子赋成原来x的左儿子 fa[ls[id]]=y; for (i=id;i;i=fa[i]) size[i]--; size[y]=size[ls[y]]+size[rs[y]];//y的子树大小需要更新 } else //最复杂的情况 //如果id右儿子不是右侧最小的点 { for (i=fa[y];i;i=fa[i]) size[i]--;//注意到变换完之后y到root路径上每个点的size都减少了1 int tt=fa[y]; //先把y提出来(tt即为右侧最小点的父亲) if (ls[tt]==y)//如果tt的左儿子是y { ls[tt]=rs[y];//现在左儿子变为y的右儿子 fa[rs[y]]=tt; } else { rs[tt]=rs[y]; fa[rs[y]]=tt; } //再来提出x if (ls[t]==x) { ls[t]=y; fa[y]=t; ls[y]=ls[id]; rs[y]=rs[id]; } else { rs[t]=y; fa[y]=t; ls[y]=ls[id]; rs[y]=rs[id]; } size[y]=size[ls[y]]+size[rs[y]]+1;//更新一下size } } } int main() { scanf("%d",&n); for (i=1;i<=n;++i) scanf("%d",&a[i]); build1(); printf("%d ",Findkth(root,2));//查询第k大的权值是什么 del(4); printf("%d ",Findkth(root,2)); }
对每个节点在多记一个size[x]表示x这个节点子树里节点的个数。
举个例子:
*size6
/
*size1*size4
/|
* * *
从根开始,如果右子树的size ≥ k,就说明第k大值在右侧,
往右边走,如果右子树size + 1 = k,那么说明当前这个点就是第k大值。
否则,把k减去右子树size + 1,然后递归到左子树继续操作。
size维护:
插入一个结点时,遍历到的点都+1
删除时:1.直接删除,其上所有父亲size--;
- 只有一个儿子,沿id的值,它的所有父亲-1
- 两个儿子:从y的父亲开始,向上删除每个父亲的size直到根;
遍历:
注意到权值在根的左右有明显区分:
做一次中序遍历就可以从小到大把所有树排好了。

先访问到最左,直到下方无儿子,输出,然后再访问右儿子
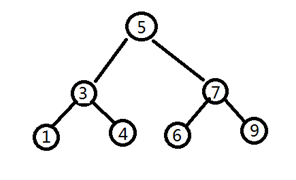
1345679
回到最初的题:
一个良好的例子:31245
一个糟糕的例子 :12345
二叉搜索树每次操作访问O(h)个节点。
总结:
既然他的复杂度与直接暴力删除类似,那我们为什么要学他呢?
1.因为教学安排里有(大误).
2.这是第一个能够利用树的中序遍历的性质的数据结构。
3.扩展性强。更复杂的splay,treap,SGT等都基于二叉搜索树,只是通过一些对树的形态的改变来保证操作的复杂度,且保持树中序遍历的形态。
4.因为数据很水。随机数据还是很强势的。
二叉堆:
满二叉树:除最后一层都是满的;
用二叉搜索树还是没法解决我们之前的问题。
堆是一种特殊的二叉树,并且是一棵满二叉树。(这和我学的不太一样qwq)
第i个节点的父亲是i/2,这样我们就不用存每个点的父亲和儿子了。
二叉搜索树需要保持树的中序遍历不变,而堆则要保证每个点比两个儿子的权值都小。
如何建堆:
最快捷的方法:直接O(nlogn)排序qwq;
据说堆得所有操作几乎都是O(logn)的
求最小值
可以发现每个点都比两个儿子小,那么最小值显然就是a[1]辣,是不是很simple啊。
simple是simple,但是要写代码啊qwq
注意到二叉搜索树中的复杂度都是O(h)
在堆中我们也想让复杂度是O(h)
= O(log n).
这样一来我们就要让树的形态不变,所以我们每次改变的都是权值的位置。
插入一个值:小根堆
首先我们先把新加入的权值放入到n + 1的位置。
然后把这个权值一路往上比较,如果比父亲小就和父亲交换.
注意到堆的性质在任何一次交换中都满足。
实现:
如果某个点x比父亲(position[x]/2)小,就和父亲交换位置
修改一个点的权值:
咦,为什么没有删除最小值?
删除最小值只要把一个权值改到无穷大就能解决辣
比较简单的是把一个权值变小。
那只要把这个点像插入一样向上动就行了。
变大权值:
那么这个点应该往子树方向走。
看看这个点的两个儿子哪个比较小。
如果小的那个儿子的权值比他小,就交换。
直到无法操作
定位问题:
一般来说,堆的写法不同,操作之后堆的形态不同.
所以一般给的都是改变一个权值为多少的点
假设权值两两不同,再记录一下某个权值现在哪个位置。
在交换权值的时候顺便交换位置信息
删除权值:
理论上:把需要被删除的点赋成inf,然后下沉一次;
但是,这样的话会有很多的inf在最下层,所以我们可以把队尾元素移到最上方,再下沉一下即可。一般删除最小的值。
一种新的建堆方法:
倒序的把每个结点都下沉。
显然它是对的qwq;
复杂度n/2(倒数第二层,显然只需下沉一次) + n/4 * 2 (倒数第二层,显然需下沉两次)+ n/8 * 3 + .... = O(n)
#include<cstdio> #include<algorithm> #include<cstring> #include<iostream> #include<cstring> #include<string> #include<cmath> #include<ctime> #include<set> #include<vector> #include<map> #include<queue> #define N 300005 #define M 8000005 #define ls (t<<1) #define rs ((t<<1)|1) #define mid ((l+r)>>1) #define mk make_pair #define pb push_back #define fi first #define se second using namespace std; int i,j,m,n,p,k,a[N]; int FindMin() { return a[1]; } void build1()//暴力建堆 { sort(a+1,a+n+1); } void up(int now)//上浮 { while (now&&a[now]<a[now/2]) swap(a[now],a[now/2]),now/=2; } void ins(int x) { a[++n]=x; up(n); } void down(int now)//下沉 { while (now*2<=n) { if (now*2==n) { if (a[now]>a[now*2]) swap(a[now],a[now*2]),now*=2; } else { if (a[now]<=a[now*2]&&a[now]<=a[now*2+1]) break; if (a[now*2]<a[now*2+1]) swap(a[now],a[now*2]),now*=2; else swap(a[now],a[now*2+1]),now=now*2+1; } } } void del(int x) { swap(a[x],a[n]); --n; up(x); down(x); } void change(int x,int val) { if (a[x]>val) { a[x]=val; up(x); } else { a[x]=val; down(x); } } void build2()//下沉建堆 { for (i=n/2;i>=1;--i) down(i); } int main() { scanf("%d",&n); for (i=1;i<=n;++i) scanf("%d",&a[i]); build2(); }
eg2(堆排):洛谷快速排序可以了解一下


#include<iostream> #include<algorithm> #include<cstdio> #include<cstring> using namespace std; int n,a,b; int heap[100010],heap_size; int get(){ int now,next,res; res=heap[1]; heap[1]=heap[heap_size--]; now=1; while(now*2<=heap_size){ next=now*2; if(next<heap_size&&heap[next+1]<heap[next])next++; if(heap[now]<=heap[next])break; swap(heap[now],heap[next]); now=next; } return res; } void put(int d){ int now,next; heap[++heap_size]=d; now=heap_size; while(now>1){ next=now/2; if(heap[now]>=heap[next])break; swap(heap[now],heap[next]); now=next; } } int main(){ scanf("%d",&n); for(int i=1;i<=n;i++){ scanf("%d",&a); put(a); } for(int i=1;i<n;i++) printf("%d ",get()); printf("%d",get()); return 0; }
丑数:
丑数指的是质因子中仅包含2, 3, 5, 7的数,最小的丑数是1,求前k个丑数。
K ≤ 6000.
part1:暴力出奇迹,打表水万物。
part2:正经的:

考虑递增来构造序列:
举个eg,已经选中了x,那么接下来可以塞进去x*2,x*3,x*5,x*7。
然后考虑重复的情况,如果已经在堆里,就不在插入惹。
Queue
每次都要写堆太麻烦了有没有什么方便的。
在C + +的include < queue >里有一个叫priority queue的东西。(优先队列)(疑似大根堆)
#include<queue>
using namespace std;
priority_queue<类型> 队列名
Q.push()
Q.top()
Q.pop()
Q.clear()清空
set
#include<set>
using namespace std;
//元素不可重,相同的元素为一个
set<int>st;
st.insert(k)//插入
st.erase(x)//删除
st.fnd(r)//看某个值是否存在
st.lower/upper bound()//咱用的那个
st.begin()/st.end()//返回指向第一个元素的迭代器/返回指向最后一个元素的迭代器
set<int>::iterator it=st.lower_bound(x);//表示一个下标,代替了下标的功能
++it;- -it;
int x=*it;
实施维护一个有序的数组。
区间RMQ问题:
区间RMQ问题是指这样一类问题。
给出一个长度为N的序列,我们会在区间上干的什么(比如单点加,区间加,区间覆盖),并且询问一些区间有关的信息(区间的和,区间的最大值)等。
最简单的问题:
给出一个序列,每次询问区间最大值.
N ≤ 100000, Q ≤ 1000000
ST表:一种处理静态区间可重复计算(一般只最大值和最小值)的数据结构;
求3~5的最大值
可以求3~4的最大值,再求出4~5最大值,然后再求
ST表的思想是先求出每个[i, i + 2k)的最值。
注意到这样区间的总数是O(N log N)的
log N这一复杂度是OI最常用复杂度。
而sqrt(N)是OI最玄学的复杂度。
预处理:不妨令f[i][j]为区间[i,i+2j)的某个最值(楼下是最小值)
那么首先fi,0的值都是它本身。
而fi,j = min(fi,j−1, fi+2j−1,j−1)
即:
一段i~i+2j的区间 i— — — — — — — — — — — — — —i+2j
那么它的最小值就为: i— — — — — — —i+2j-1— — — — — — —i+2j
这两段区间最小值中更小的即fi,j = min(fi,j−1, fi+2j−1,j−1)
O(N log N)

k=log2(r-l+1)
区间长度r-l+1;
#include<cstdio> #include<algorithm> #include<cstring> #include<iostream> #include<cstring> #include<string> #include<cmath> #include<ctime> #include<set> #include<vector> #include<map> #include<queue> #define N 300005 #define M 8000005 #define K 18 #define ls (t<<1) #define rs ((t<<1)|1) #define mid ((l+r)>>1) #define mk make_pair #define pb push_back #define fi first #define se second using namespace std; int i,j,m,n,p,k,ST[K+1][N],a[N],Log[N]; int Find(int l,int r) { int x=Log[r-l+1]; return max(ST[x][l],ST[x][r-(1<<x)+1]); //注意到对于[l,r],[l,l+2^x-1],[r-2^x+1,r]并起来是[l,r] } int main() { scanf("%d",&n); for (i=1;i<=n;++i) scanf("%d",&a[i]); for (i=1;i<=n;++i) ST[0][i]=a[i];//预 处 理。提前处理好一部分ST for (i=1;i<=K;++i) for (j=1;j+(1<<i)-1<=n;++j) ST[i][j]=max(ST[i-1][j],ST[i-1][j+(1<<(i-1))]); //ST[i][j]为从j开始的长度为2^i的区间的最大值 //显然[j,j+2^i)=[j,j+2^(i-1))+[j+2^(i-1),j+2^i)=max(ST[i-1][j],ST[i-1][j+2^(i-1)]) for (i=1;(1<<i)<N;++i) Log[1<<i]=i; //令Log[x]为比x小的最大的2^y for (i=1;i<N;++i) if (!Log[i]) Log[i]=Log[i-1]; printf("%d ",Find(1,3)); }
我们将两个区间合并 因为取最大值 所以合并起来好操作 那个 STlist[][]的定义不是st[i][j]=max{a[i]->a[i+(2^j)-1]}嘛 那么st[i][j]=max(st[i][j-1],st[i+(2^(j-1))][j-1])就可以推导出来 意思是st[i][j]可以分成左右两个区间处理 然后如果j=0,那么st[i][j]=max(a[i],a[i]) 这是预处理 向下合并的时候,我们可以写一下 //Log2[]数组也要预处理,这个待会再说 for (register int i=1;i<=Log2[n];i++)//这个控制的是第二维 { for (register int l=1;l+(1<<i)-1<=n;l++)//这个控制的是左端点 { //整个的区间 st[l][i]=max(st[l][i-1],st[l+(1<<(i-1))][i-1]); //这个重点理解一下 } } 最后讲一下Log2的推法(直接背过算了) int Log2[1000001]={0,0,1};//log2(0)不存在,log2(1)=0,log2(2)=1 inline void Init_log2(int r) { for (register int i=3;i<=r;i++) { Log2[i]=Log[i>>1]+1; } } 于是我们怎么询问呢 一个区间[l->r],我们可以拆分成两个重叠的区间(反正取最大最小值不管) inline long long query(int l,int r) { int k=Log2[r-l+1];//区间长度向下去一个log return max(st[l][k],st[r-(1<<k)][k]);//即可 //l->2^k,(r-2^k)->r }
eg

线段树:
其实线段树被称为区间树比较合适.
本质是一棵不会改变形态的二叉树.
树上的每个节点对应于一个区间[a, b](也称线段),a,b通常为整数
同一层的节点所代表的区间,相互不会重叠
同一层节点所代表的区间,加起来是个连续的区间
对于每一个非叶结点所表示的结点[a,b],其左儿子表示的区间为[a,(a+b)/2],右儿子表示的区间为[(a+b)/2+1,b](除法去尾取整)
叶子节点表示的区间长度为1.
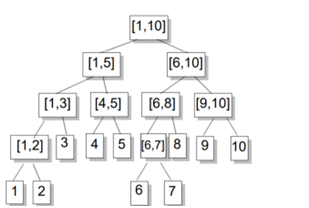
同一层的结点区间长度相差不大于1
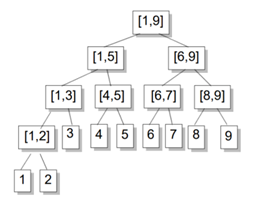
注意到线段树的结构与分治结构差不多深度也是O(log N)的
区间拆分:
区间拆分是线段树的核心操作。我们可以将一个区间[a, b]拆分成若干个节点,使得这些节点代表的区间加起来是[a, b],并且相互之间不重叠.
所有我们找到的这些节点就是”终止节点
从根节点[1, n]开始,考虑当前节点是[L, R].
如果[L, R]在[a, b]之内,那么它就是一个终止节点.
否则,分别考虑[L, Mid],[Mid
+ 1, R]与[a, b]是否有交,递归两边继续找终止节点.
举个例子:在1~9中找2~8
判断2~8和左右是否有交(显然是有的)
所以左右两边都要递归
4,5完全被2~8包含,故停下对4,5的访问,再递归1~3
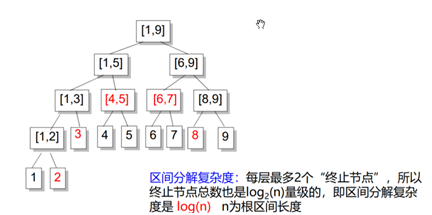
解题方法:

例1:


#include<cstdio> #include<algorithm> #include<cstring> #include<iostream> #include<cstring> #include<string> #include<cmath> #include<ctime> #include<set> #include<vector> #include<map> #include<queue> #define N 300005 #define M 8000005 #define ls (t*2) #define rs (t*2+1) #define mid ((l+r)/2) #define mk make_pair #define pb push_back #define fi first #define se second using namespace std; int i,j,m,n,p,k,add[N*4],sum[N*4],a[N],ans,x,c,l,r; void build(int l,int r,int t)//建树 { if (l==r) sum[t]=a[l]; else { build(l,mid,ls); build(mid+1,r,rs); sum[t]=max(sum[ls],sum[rs]); //预先处理区间[l,r]的最大值 } } void modify(int x,int c,int l,int r,int t) //将a[x]修改为c,然后需要对所有包含x的区间进行更新 { if (l==r) sum[t]=c; //只有一个点的时候可以直接计算 else { if (l<=x&&x<=mid) modify(x,c,l,mid,ls); else modify(x,c,mid+1,r,rs); sum[t]=max(sum[ls],sum[rs]);//回溯的时候[l,mid],[mid+1,r]的答案已经算出,可以利用两个儿子进行更新 } } void ask(int ll,int rr,int l,int r,int t) //询问[ll,rr]这个区间的最大值,l,r,t表示的是当前线段树上位置代表的区间[l,r]和编号t { if (ll<=l&&r<=rr) ans=max(ans,sum[t]); //找到了一个完整被[ll,rr]区间包含的区间,直接把答案记进去 else { if (ll<=mid) ask(ll,rr,l,mid,ls); //如果和左儿子有交就往左儿子走 if (rr>mid) ask(ll,rr,mid+1,r,rs); //如果和右儿子有交就往右儿子走 } } int main() { scanf("%d",&n); for (i=1;i<=n;++i) scanf("%d",&a[i]); build(1,n,1); modify(1,5,1,n,1); ask(1,5,1,n,1); }
poj 3264


poj 3468
给定Q个数A1, ..., AQ,多次进行以下操作:
1.对区间[L, R]中的每个数都加n.
2.求某个区间[L, R]中的和.
Q ≤ 100000
如果只记录区间的和?
进行操作1的时候需要O(N)的时间去访问所有的节点.
考虑多记录一个值inc,表示这个区间被整体的加了多少.
延迟更新:
信息更新时,未必要真的做彻底的更新,可以只是将应该如何更新记录下来,等到真正需要查询准确信息时,才去更新足以应付查询的部分
在区间增加时,如果要加的区间正好覆盖一个节点,则增加其节 点的inc值和sum值,不再往下走.
在区间询问时,还是采取正常的区间分解.
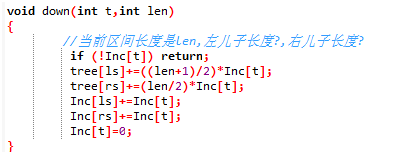
在上述两种操作中,如果我们到了区间[L, R]还要接着往下走,并且inc非0,说明子区间的信息是不对的,我们将inc传送到左儿子和右儿子上,并将inc赋成0,即完成了一次更新
eg:
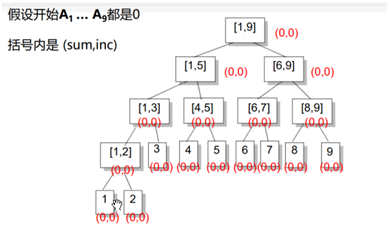
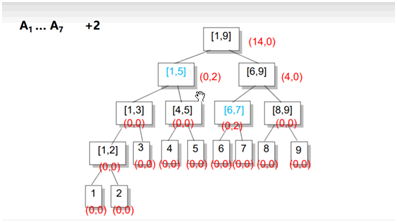
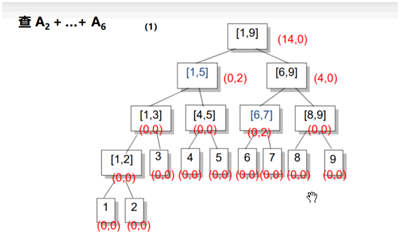
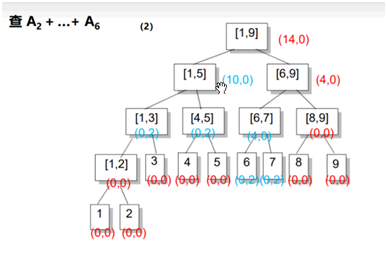
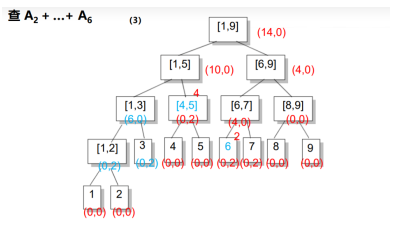
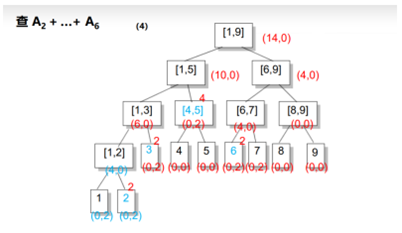
右儿子区间长度len/2,左儿子区间:(len+1)/2;
#include<cstdio> #include<algorithm> #include<cstring> #include<iostream> #include<cstring> #include<string> #include<cmath> #include<ctime> #include<set> #include<vector> #include<map> #include<queue> #define N 300005 #define M 8000005 #define ls (t*2) #define rs (t*2+1) #define mid ((l+r)/2) #define mk make_pair #define pb push_back #define fi first #define se second using namespace std; int i,j,m,n,p,k,lazy[N*4],sum[N*4],a[N],ans,x,c,l,r; void build(int l,int r,int t) { if (l==r) sum[t]=a[l]; else { build(l,mid,ls); build(mid+1,r,rs); sum[t]=sum[ls]+sum[rs]; } } void down(int t,int len) //对lazy标记进行下传 { if (!lazy[t]) return; sum[ls]+=lazy[t]*(len-len/2); sum[rs]+=lazy[t]*(len/2); lazy[ls]+=lazy[t]; lazy[rs]+=lazy[t]; lazy[t]=0; } void modify(int ll,int rr,int c,int l,int r,int t) //[ll,rr]整体加上c { if (ll<=l&&r<=rr) { sum[t]+=(r-l+1)*c; //对[l,r]区间的影响就是加上了(r-l+1)*c lazy[t]+=c; } else { down(t,r-l+1); if (ll<=mid) modify(ll,rr,c,l,mid,ls); if (rr>mid) modify(ll,rr,c,mid+1,r,rs); sum[t]=sum[ls]+sum[rs]; } } void ask(int ll,int rr,int l,int r,int t) //对于区间[l,r]进行询问 { if (ll<=l&&r<=rr) ans+=sum[t]; //代表着找到了完全被包含在内的一个区间 else { down(t,r-l+1); if (ll<=mid) ask(ll,rr,l,mid,ls); if (rr>mid) ask(ll,rr,mid+1,r,rs); } } int main() { scanf("%d%d",&n,&m); for (i=1;i<=n;++i) scanf("%d",&a[i]); build(1,n,1); }
下传到儿子
poj2528
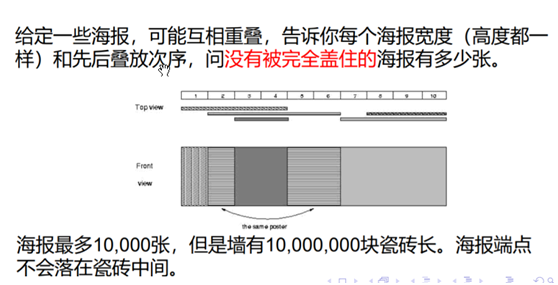
首先我们对数据进行一些处理,使得1kw的砖块数量减少。
我们将海报的所有的端点都拿出来,排序去重。
对于两个端点之间的部分,每块砖要么完全经过他们,要么完全不经过它们,

将两端点之间的部分当成一块砖,然后就可以把砖块数量减到4w块
从最底层的海报开始,一张一张往上贴
对于一个区间[L, R],我们记录的信息是这个区间整体被第几张海报覆盖了,初始值设为−1.
对于一张包含[L, R]的海报i,我们就只需要把[L, R]里面所有的位置都赋成i就可以了.
注意利用区间分解和延迟更新的方法.
本题中是否会有标记时间冲突的问题?不会
标记下传,只可能是后来的覆盖先来了
zyb画画:
给出长度为N的序列A,
Q次操作,两种类型:
(1 x v),将Ax改成v.
(2 l r) 询问区间[l, r]中有多少段不同数。例
如2 2 2 3 1 1 4,就是4段。
N, Q ≤ 100000.
线段树上的每个节点都维护三个信息:
这段区间有多少段不同的数,最右边的数,最左边的数.
合并的时候,如果中间接上的地方相同,则段数−1.
非常简单的线段树合并操作.时间复杂度O((N + Q) log N).
树状数组:
是一种用来求前缀和的数据结构.
记lowbit(x)为x的二进制最低位.
例子:lowbit(8) = 8, lowbit(6) = 2
记fi是i的最低位.
若i是奇数,fi =
1,否则fi = fi/2 * 2.
麻烦?lowbit(i)
= i& - i.
对于原始数组A,我们设一个数组C.
C[i]=a[i-lowbit(i)+1]+...+a[i]
i > 0的时候C[i]才有用.C就是树状数组

树状数组用于解决单个元素经常修改,而且还反复求不同的区间和的情况
求和
树状数组只能够支持询问前缀和.
我们先找到C[n],然后我们发现现在,下一个要找的点是n
- lowbit(n),然后我们不断的减去lowbit(n)并累加C数组.
我们可以用前缀和相减的方式来求区间和.
询问的次数和n的二进制里1的个数相同.则是O(log N).
更新:
现在我们要修改Ax的权值,考虑所有包含x这个位置的区间个数.
从C[x]开始,下一个应该是C[y = x + lowbit(x)],再下一个是C[z = y + lowbit(y)]...
注意到每一次更新之后,位置的最低位1都会往前1.总复杂度也为O(log N).
eg2:
求一个数组A1, A2, ..., An的逆序对数.
n ≤ 100000, |Ai| ≤ 109.
solution:
我们将A1, ..., An按照大小关系变成1...n.这样数字的大小范围在[1, n]中.(离散化)
维护一个数组Bi,表示现在有多少个数的大小正好是i.
从左往右扫描每个数,对于Ai,累加BAi+1...Bn的和,同时将BAi加1.
时间复杂度为O(N
log N)
unique(a,a+n+1)-(a+1); //1~n中所有数,去重后的元素个数;去重后指针的位置
lower_bound找第几个位置
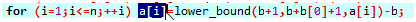 返回在整个数组里是第几个数
返回在整个数组里是第几个数
树及LCA问题:
LCA:
在一棵有根树中,树上两点x, y的LCA指的是x, y向根方向遇到到第一个相同的点
我们记每一个点到根的距离为deepx.
注意到x, y之间的路径长度就是deepx + deepy - 2 * deepLCA.
LCA原始求法:
两个点到根路径一定是前面一段不一样,后面都一样.
注意到LCA的深度一定比x,
y都要小.
利用deep,把比较深的点往父亲跳一格,直到x,
y跳到同一个点上.
这样做复杂度是O(len)
考虑一些静态的预处理操作.
像ST表一样,设fai,j为i号点的第2j个父亲。
自根向下处理,容易发现fai,j = fafai,j-1,j-1.
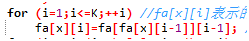
求第k个祖先
首先,倍增可以求每个点向上跳k步的点.
利用类似快速幂的想法.
每次跳2的整次幂,一共跳log次.

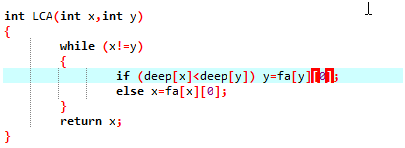
求LCA:
首先不放假设deepx> deepy.
为了后续处理起来方便,我们先把x跳到和y一样深度的地方.
如果x和y已经相同了,就直接退出
否则,由于x和y到LCA的距离相同,倒着枚举步长,如果x, y的第2j个父亲不同,就跳上去.这样,最后两个点都会跳到离LCA距离为1的地方,在跳一步就行了.
时间复杂度O(N log N).
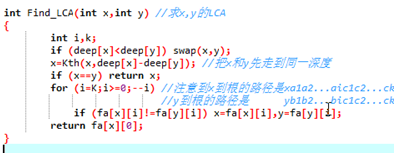
如果fa相同,return,否则就向上跳一步。
考虑二分也可以(从根节点到deepy二分)
总结
LCA能发挥很大的用处,具体可以去咨询后天教你们图论的学长.
倍增这一算法的时空复杂度分别
为O(N
log N) - O(log
N) O(N
log N)
#include<cstdio> #include<algorithm> #include<cstring> #include<iostream> #include<cstring> #include<string> #include<cmath> #include<ctime> #include<set> #include<vector> #include<map> #include<queue> #define N 300005 #define M 8000005 #define K 18 #define ls (t<<1) #define rs ((t<<1)|1) #define mid ((l+r)>>1) #define mk make_pair #define pb push_back #define fi first #define se second using namespace std; int i,j,m,n,p,k,fa[N][K+1],deep[N]; vector<int>v[N]; void dfs(int x) //dfs求出树的形态,然后对fa数组进行处理 { int i; for (i=1;i<=K;++i) //fa[x][i]表示的是x向父亲走2^i步走到哪一个节点 fa[x][i]=fa[fa[x][i-1]][i-1]; //x走2^i步相当于走2^(i-1)步到一个节点fa[x][i-1],再从fa[x][i-1]走2^(i-1)步 for (i=0;i<(int)v[x].size();++i) { int p=v[x][i]; if (fa[x][0]==p) continue; fa[p][0]=x; deep[p]=deep[x]+1; //再记录一下一个点到根的深度deep_x dfs(p); } } int Kth(int x,int k) //求第k个父亲,利用二进制位来处理 { for (i=K;i>=0;--i) //k可以被拆分成logN个2的整次幂 if (k&(1<<i)) x=fa[x][i]; return x; } int Find_LCA(int x,int y) //求x,y的LCA { int i,k; if (deep[x]<deep[y]) swap(x,y); x=Kth(x,deep[x]-deep[y]); //把x和y先走到同一深度 if (x==y) return x; for (i=K;i>=0;--i) //注意到x到根的路径是xa1a2...aic1c2...ck //y到根的路径是 yb1b2...bic1c2...ck 我们要做的就是把x和y分别跳到a_i,b_i的位置,可以发现这段距离是相同的. if (fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i]; return fa[x][0]; } int main() { scanf("%d",&n); for (i=1;i<n;++i) { int x,y; scanf("%d%d",&x,&y); v[x].pb(y); v[y].pb(x); } dfs(1); printf("%d ",Find_LCA(3,5)); }
并查集:
简单例题:

solution:


操作示例:
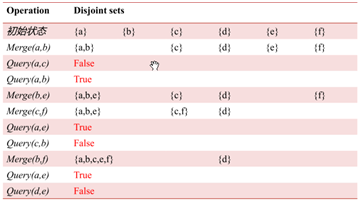
考虑用有根树来维护集合:
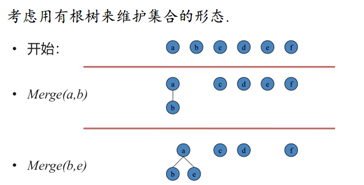
利用树形结构,记录fai=j表示i的父亲为j
若fai = i,则说明i是根节点,一开始fai = i.

利用树形结构解决询问:
询问Query(a,
b):调用两次Getroot函数,判断两个根是否相同.
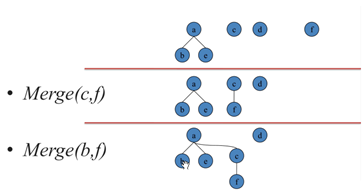
修改Merge(a, b) :,同样调用Getroot找到a, b的根,如果相同就不管,否则将a的根的父亲设为b.
注意到Getroot的单次复杂度可能达到O(N).
尝试优化:
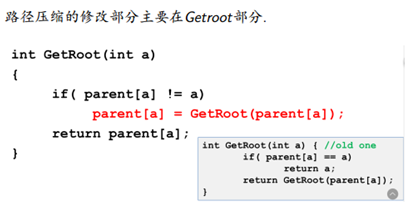
- 路径压缩:
第一种优化看起来很玄学,我们在寻找一个点的顶点的时候,显然可以把这个点的父亲赋成他的顶点,也不会有什么影响.
看起来玄学,但是他的复杂度是O(N log N)的。
证明很复杂,有兴趣的同学可以自行翻阅论文。
- 按秩合并:
对每个顶点,再多记录一个当前整个结构中最深的点到根的深度deepx.
注意到两个顶点合并时,如果把比较浅的点接到比较深的节点上.
如果两个点深度不同,那么新的深度是原来较深的一个.
只有当两个点深度相同时,新的深度是原来的深度+1.
注意到一个深度为x的顶点下面至少有2x个点,所以x至多为log
N
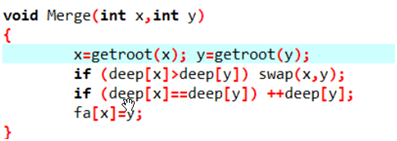
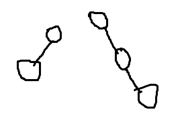
合并=>法1: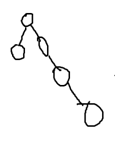 显然不够优秀
显然不够优秀
=>法2: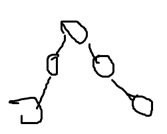 比较优秀
比较优秀
比较:
无论是时间,空间,还是代码复杂度,路径压缩都比按秩合并优秀.
值得注意的是,路径压缩中,复杂度只是N次操作的总复杂度为O(N
log N)。
按秩合并每一次的复杂度都是严格O(log N)的.
noi2015传送
有N个变量,M条语句,每条语句为xi = xj,或者xi <>
xj,
询问这M条语句是否都有可能成立.
N ≤ 109, M ≤ 100000.
先用离散化处理出所有可能出现的变量.
可以把相同变量用并查集合并(merge)起来.
对于一条不同的语句,判断它的两个变量是否在同一个块里
from洛谷题解:
先排序,把所有e==1的操作放在前面,然后再进行e==0的操作,在进行e==1的操作的时候,我们只要把它约束的两个变量放在同一个集合里面即可。在e==0,即存在一条不相等的约束条件,对于它约束的两个变量,如果在一个集合里面,那就不可能满足!如不相等的约束条件都满足,那就YES。
poj1611
有n个学生,编号0到n
- 1, 以及m个团体,0
< n ≤ 30000, 0 ≤ m
≤ 500).一个学生可以属于多个团体,也可以不属于任何团体.一个学生疑似疑似患病,则它所属的整个团体都疑似患病。
已知0号学生疑似患病,以及每个团体都由哪些学生构成,
求一共多少个学生疑似患病.

solution1:互相感染的人,应该属于同一个集合。最终问0所在的集合有几个元素
solution2:考虑把每个人变成一个点.然后同一个组里的人相互之间有连边,问和0号点连通的有多少点.边数有m * n2条,无法接受,我们给每个团体建一个点,然后所有组里的人向它连边,就把边数减到了n * m条.
用BFS找出连通块
poj.1998
有N(N
≤ 30, 000)堆方块,开始每堆都是一个方块.方块编号1N. 有两种操作:
M x y : 表示把方块x所在的堆,拿起来叠放到y所在的堆上。
C x : 问方块x下面有多少个方块。
操作最多有P(P
≤ 100, 000)次。对每次C操作,输出结果。
solution:
首先由于我们要合并的是两个堆,那么至少要维护一个fai,即代表每个方块所在的堆是哪一个.
那么,我们还需要维护一个underx,表示x这个方块下面有多少方块,初始的时候underx = 0.
那么要怎么维护underx呢?
当每次合并x, y时,我们强制将x的父亲连为y,并将underx加上y里面数的个数.
再维护一个sizex表示x这个并查集的大小,只需要在Merge时维护,underx在Merge和Getroot时都要更新.

程序自动分析改:
有N个变量,每个变量只有0, 1两种取值.有M条语句,每条
语句为xi = xj,或者xi <>
xj,询问这M
条语句是否都有可能成立.
N ≤ 109, M
≤ 100000
solution:
要注意一下只有0, 1时的区别.
把一个点拆成x, x′两个点。
如果y与x同一组,说明y与x相同.
如果y与x′一组,说明y与x不同.
那么只需要xi <>
xj时i向j′连边,最后查询x和x′是否在同一组中即可.