写在算法前面:
前向星存图(一个神奇的超越邻接矩阵的存在)
首先讲一下需要定义的一些东西??
1.head数组:head[点数]:head[i]表示以当前点i为起点的最后一条边(这里的最后指的是编号【我们按输入顺序给边编一个号】)。![]()
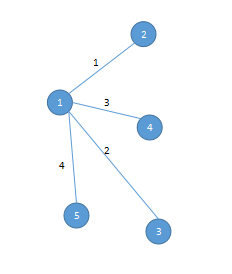
这个图即为head[1]=4,表示以1为起点的边的最后一条是点1—>点5编号为4的边;
2.num_edge,表示边的总个数;
3.结构体:
struct Edge{ int next,to,dis; }edge[边数];
这里,edge[i].next表示上一条以i为起点的边:![]() :
:
还是上面那个图,这里edge[4].next=3;
edge[i].to表示这条边i的终点;
edge[i].dis表示这条边的权值;
存图
void addedge(int from,int to,int dis){ num_edge++;//因为存入一条边,总边数+1; edge[num_edge].next=head[from];//新存入一条以from为起点的边,之前的以from为起点的最后一条边变成了新边的上一条边 edge[num_edge].to=to;//存终点 edge[num_edge].dis=dis;//存权值 head[from]=num_edge;//存入一条以from为起点的边,那么现在以from为起点的最后一条边就是新存入的边 }
提醒:如果要存的是无向图,进行程序时应该:addedge(from,to,dis),addedge(to,from,dis)各跑一遍,所开空间也要*2;
大概是讲完了链式前向星存图;
spfa
算法思想:
1.运用队列的思想,先把起点入队,更新起点能够到达的点,更新这些点到起点的伪最短路(因为可能还有更短情况)然后把得到更新的点中不在队列里的加入队列,以便更新其他点。
2.当前更新的是伪最短路即可能会有更优情况
eg:起点是1,1到6距离为7,加入队列dis[6]=7,而1到7距离为2,7到6距离为3,会将dis[6]更新为2+3=5。所以一遍一遍查,最后将会是最短路。
时间复杂度大约是O(ke),稀疏图中k约等于2,但是毒瘤数据会把复杂度卡成O(nm);
spfa在存图基础上再开vis[点数]查询某个点是否已经在队列里,避免重复入队(请注意,是是否在队列里 队列里 队列里)
dis[点数]用来存某个点到起点的最短路;
以洛谷p3371【模板】单源最短路径(弱化版) 为例纸(标准的过不去qwq)
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #include<cmath> #include<queue> using namespace std; const int inf=2147483647;//题目要求的初始值 queue <int> q;//定义一个队列q int n,m,s; int head[10010],num; int vis[10010],dis[10010]; struct Edge{ int next,to,dis; }edge[500010]; void addedge(int from,int to,int dis){//加边 num++; edge[num].next=head[from]; edge[num].to=to; edge[num].dis=dis; head[from]=num; } void spfa(){ for(int i=1;i<=n;i++){//首先初始化,将所有点的dis赋值为2147483647,所有点都不在队列里,vis为0 dis[i]=inf; vis[i]=0; } q.push(s);//把起点入队 dis[s]=0;//起点到起点,最短路为0 vis[s]=1;//入队了,vis变为1 while(!q.empty()){//开始循环 int u=q.front(); q.pop();//把队首元素出队 vis[u]=0;//出队了,vis重置为0(因为可能还有更近的下次还能循环到) for(int i=head[u];i;i=edge[i].next){//遍历以u为起点的所有遍 int v=edge[i].to;//v为终点 if(dis[v]>dis[u]+edge[i].dis){//如果之前的最短路比由u点出发再”拐弯“的点的要大,显然他不是最短,更新他 dis[v]=dis[u]+edge[i].dis; if(!vis[v]){//如果终点不在队列里,入队 q.push(v); vis[v]=1; } } } } } int main(){ scanf("%d%d%d",&n,&m,&s); int u,v,w; for(int i=1;i<=m;i++){ scanf("%d%d%d",&u,&v,&w);//输入起点终点权值 addedge(u,v,w);//加边 } spfa();//核心 for(int i=1;i<=n;++i) { if(i==s) printf("0 "); else printf("%d ",dis[i]); } return 0; }
end-