4.4下午:矩阵qwq
- part1矩阵乘法:
- 概念:
一个m×p的矩阵A 乘 一个p×n的矩阵B 得到一个矩阵一个m×n的矩阵AB
其中:
矩阵乘法满足结合律、分配率,不满足交换律
矩阵乘法—solution:
struct m{ int a[2][2]; }; m operator *(m a,m b){ m c; for(int i=0;i<=1;i++) for(int j=0;j<=1;j++){ c.a[i][j]=0; for(int k=0;k<=1;k++) c.a[i][j]=(c.a[i][j]+a.a[i][k]*b.a[k][j])%p; }return c;}
eg1:斐波那契数列
【题目背景】
yy最近在数学课上学了斐波那契数列,已知斐波那契数列满足f(n)=f(n-1)+f(n-2)且f(1)=f(2)=1,现在yy的老师想要考考他们,老师随意给出一个数k,要大家一个个的回答他斐波那契数列的第k项,下一个就轮到yy了,但 yy做了半天,怎么也想不到做法,请你写一个程序帮助yy快速的算出第k项。
【输入格式】
输入只有一行,为这个数k。
【输出格式】
只有一行,输出斐波那契数列的第k项(取模1e9+7)
【输入样例】 【输出样例】
15 610
#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> using namespace std; long long p=1000000007; int k; struct m{ int a[2][2]; }; m operator *(m a,m b)//矩阵乘法的标程qwq { m c; for(int i=0;i<=1;i++) for(int j=0;j<=1;j++){ c.a[i][j]=0;//先把全部的值都赋为0 for(int k=0;k<=1;k++) c.a[i][j]=(c.a[i][j]+a.a[i][k]*b.a[k][j])%p;
//eg: 1.c.a[0][0]=(c.a[0][0]+a.a[0][0]*b.a[0][0])%pp;
// 2.c.a[0][0]=(c.a[0][0]+a.a[0][1]*b.a[1][0])%pp;
//综上:c.a[0][0]=(a.a[0][1]*b.a[1][0]+a.a[0][0]*b.a[0][0])%pp;
} return c; } int main() { cin>>k; m a; a.a[0][0]=0;a.a[1][0]=1; a.a[0][1]=1;a.a[1][1]=1; m ans; ans.a[0][0]=1;ans.a[1][0]=0; ans.a[0][1]=0;ans.a[1][1]=1;//单位矩阵,当一来用; int b=k-1; while(b){//结构体乘法 利用快速幂思想 if(b&1)ans=ans*a; a=a*a; b/=2; } int fk=(ans.a[0][1]+ans.a[0][0])%p;//ans.a[0][0]*f(1)+ ans.a[0][1]*f(2) cout<<fk<<endl; }
思路:构建转移矩阵:
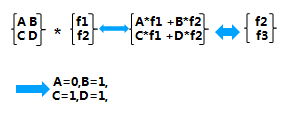
eg2:
【题目背景】
yy今天又上数学课了,这次老师又问了yy一个新问题:
计算f(n) = 4f(n-1) – 3f(n-2) + 2f(n-4) 的第k项,老师会给定这个数列的前四项,以及一个数k,老师说如果yy可以解出来就以yy的名字命名这个数列,yy很想有一个以他名字命名的数列,请你帮帮他。
【输入格式】
第一行:四个数,分别为这个数列的第1,2,3,4项;
第二行:一个数k表示要求的是这个数列的第几项。
【输出格式】
一个数,为这个数列的第k项
【输入样例】 【输出样例】
1 1 3 5 3711(不对请指正)
10
struct along{ int a[4][4]; }; along operator *(along a,along b) { along c; for(int i=0;i<=3;i++){ for(int j=0;j<=3;j++){ c.a[i][j]=0; for(int k=0;k<=3;k++) c.a [i][j]=(c.a[i][j]+a.a[i][k]*b.a[k][j])%p; } } return c; } int main() { int x,y,z,w,k; cin>>x>>y>>z>>w; cin>>k; int b=k-1; along a; a.a[0][0]=0;a.a[1][0]=1;a.a[2][0]=0;a.a[3][0]=0; a.a[0][1]=0;a.a[1][1]=0;a.a[2][1]=1;a.a[3][1]=0; a.a[0][2]=0;a.a[1][2]=0;a.a[2][2]=0;a.a[3][2]=1; a.a[0][3]=2;a.a[1][3]=0;a.a[2][3]=-3;a.a[3][3]=4;//转移矩阵 along ans; ans.a[0][0]=1;ans.a[1][0]=0;ans.a[2][0]=0;ans.a[3][0]=0; ans.a[0][1]=0;ans.a[1][1]=1;ans.a[2][1]=0;ans.a[3][1]=0; ans.a[0][2]=0;ans.a[1][2]=0;ans.a[2][2]=1;ans.a[3][2]=0; ans.a[0][3]=0;ans.a[1][3]=0;ans.a[2][3]=0;ans.a[3][3]=1;//单位矩阵 while(b){ if(b&1)ans=ans*a; a=a*a; b/=2; } int fk=(ans.a[0][0]*x+ans.a[1][0]*y+ans.a[2][0]*z+ans.a[3][0]*w)%p; cout<<fk<<endl; }//include什么的自己加吧qwq
(为什么我u盘老是丢东西啊啊啊恐惧哪天培训的东西丢光了(Dev一改代码就丢啊啊啊)自闭)
我滴思路??
1.自己搞一搞,搞出转移矩阵(至于怎么搞,可以参见eg1
ps:之前一直搞不懂的一点,就是这个奇奇怪怪的式子乘转移矩阵的k-1次方是怎么搞到的fk,后来发现fk就是那个奇奇怪怪的式子啊qwq(大概没讲明白)
2.写代码(打表一时爽)
eg3:(poj3233)
【题目背景】
yy看中了nili千古神犇zay的一包金色袋子的零食,yy决定为难一下zay,于是yy问了azy一道题:给定一个n*n的矩阵A,求A + A^2 + A^3 + … + A^k的结果。zay居然不会qwq!显然zay不能在yy面前chuchou,现在请你帮帮zay,使他快速的算出来,如果算不出来,zay的零食就是yy的了qwq
(不想写了qwqqwqqwq求助sy去了qwq什么时候更代码随缘吧qwq)
eg4:
【题目背景】
sy要去狼外婆家买markdown(尽管我也不知道为啥qwq)现在给定一个有向图,问从sy所在地恰好走k步(允许重复经过边)到达狼外婆家的最短路长度。 有向图点数<=50 k<=10^9
原题来源于hdu
【输入格式】
输入数据有多组, 每组的第一行是2个整数 n, m(0 < n <= 20, m <= 100) 表示地图上共有n个点, 为了方便起见, 点从0到n-1编号,接着有m行, 每行有两个整数 s, t (0<=s,t<n) 表示从s点能到t点, 注意图是有向的.接着的一行是两个整数T,表示有T组询问(1<=T<=100),
接下来的T行, 每行有三个整数 A, B, k, 表示问你从A 点到 B点恰好经过k个点的方案数 (k < 20), 可以走重复边。如果不存在这样的走法, 则输出0
当n, m都为0的时候输入结束
【输出格式】
计算每次询问的方案数, 由于走法很多, 输出其对1000取模的结果
【输入样例】
4 4
0 1
0 2
1 3
2 3
2
0 3 2
0 3 3
3 6
0 1
1 0
0 2
2 0
1 2
2 1
2
1 2 1
0 1 3
0 0
【输出样例】
2
0
1
3
solution:
#include <iostream> #include <cstdio> #include <algorithm> #include <cmath> #include <cstring> #include <string.h> #include <vector> #include <queue> //hdu2157 #define mod 1000 using namespace std; int n; struct matrix { int a[25][25]; void init(){ for(int j=0; j<25; ++j){ for(int t=0; t<25; ++t) a[j][t]=0; } } }p; matrix mul(matrix a1, matrix b1) { matrix q; q.init(); int t, j, k; for(j=0; j<n; ++j){ for(t=0; t<n; ++t){ for(k=0; k<n; ++k){ q.a[j][t]+=a1.a[j][k]*b1.a[k][t]; q.a[j][t]%=mod; } } } return q; } matrix f(int x) { matrix q, s=p; int t, j; for(j=0; j<n; ++j){ //构建单位矩阵 for(t=0; t<n; ++t){ if(j==t) q.a[j][t]=1; else q.a[j][t]=0; } } while(x){ if(x&1) q=mul(s, q); x=x>>1; s=mul(s, s); } return q; } int main() { int m ,t, T, s, k, s1, s2, g; while(scanf("%d%d", &n, &m)!=EOF){ if(n==0&&m==0)break; p.init(); for(t=0; t<m; ++t){ scanf("%d%d", &s, &g); p.a[s][g]=1; //有向的 } scanf("%d", &T); while(T--){ scanf("%d%d%d", &s1, &s2, &k); matrix result=f(k); printf("%d ", result.a[s1][s2]); //s1到s2的路径总数 } } return 0; }//假装是自己写的qwq
特殊矩阵的矩阵乘法qwq
- 上三角矩阵
上三角*上三角=上三角qwq
- 分块矩阵
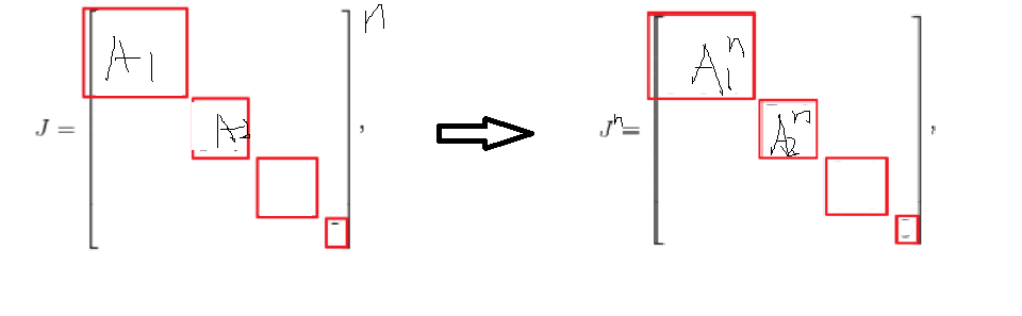
- 分块*分块=分块
- 对角矩阵(对角线有数)
- 对称矩阵
- part2高斯消元 :
原理不想讲辽,gc数学都说了,直接理解代码吧……
【题目背景】
某腾讯游戏最近新出了高斯消消乐,大佬wz想要去腾讯游戏应聘,现在公司要求写高斯消元的代码,请你帮帮他,帮他写一份代码吧qwq
【输入格式】
第一行:两个数,分别为m和n(其实他俩一样的qwq)
第2~m+1行:每行n+1个数,分别表示n个数和一个答案
【输出格式】
输出消元后的矩阵
【输入样例】 【输出样例】
没有输入样例 没有输出样例
只有求助解释check
上代码(from lh)(注释from lz):
#include<iostream> #include<algorithm> #include<cstdio> #include<cstring> #include<cmath> #include<cstdlib> using namespace std; typedef long long ll; typedef long double ld; typedef pair<int,int> pr; const double pi=acos(-1); #define rep(i,a,n) for(int i=a;i<=n;i++) #define per(i,n,a) for(int i=n;i>=a;i--) #define Rep(i,u) for(int i=head[u];i;i=Next[i]) #define clr(a) memset(a,0,sizeof a) #define pb push_back #define mp make_pair #define fi first #define sc second ld eps=1e-9; ll pp=1000000007; ll mo(ll a,ll pp){if(a>=0 && a<pp)return a;a%=pp;if(a<0)a+=pp;return a;} ll powmod(ll a,ll b,ll pp){ll ans=1;for(;b;b>>=1,a=mo(a*a,pp))if(b&1)ans=mo(ans*a,pp);return ans;} ll read(){ ll ans=0; char last=' ',ch=getchar(); while(ch<'0' || ch>'9')last=ch,ch=getchar(); while(ch>='0' && ch<='9')ans=ans*10+ch-'0',ch=getchar(); if(last=='-')ans=-ans; return ans; } //head(lh的代码头) int n,m; double a[100][100]; bool check(int k){ if(fabs(a[k][n+1])<eps)return 1;// 如果小于0,返回1 for(int i=1;i<=n;i++) if(fabs(a[k][i])>eps)return 1;//第k行的每个数都大于0 return 0; } int main(){ n=read();m=read();//m*n的矩阵, // a_i,1 a_i,2 ... a_i,n a_i,n+1 for(int i=1;i<=m;i++) for(int j=1;j<=n+1;j++)a[i][j]=read();//输入矩阵元素(因为除了这个m*n的矩阵,还要有一行答案qwq) (看洛谷题吧qwq) for(int j=1;j<=m;j++){ for(int k=1;k<=n+1;k++)cout<<a[j][k]<<" "; puts(""); }//先把矩阵输出辽一遍 int flag=0; for(int i=1;i<=n;i++){ int t=i; while(a[t][i]==0 && t<=n)t+=1; if(t==n+1){ flag=1; continue; }//if判断是否有一行全为0,如果全为0 那么我们就少了至少1个方程,那么这个方程显然无唯一解 for(int j=1;j<=n+1;j++)swap(a[i][j],a[t][j]);//交换第i行和第t行的值,目的在于交换第i行和第t行后可以使a[1][1]!=0 double kk=a[i][i];//找到对角线qwq for(int j=1;j<=n+1;j++)a[i][j]/=kk;//把这一行的每一项都除以对角线,使得对角线为1 for(int j=1;j<=m;j++) //这里真的要详细地讲一讲咯 if(i!=j){//首先i!=j这样就不再消对角线上的数了 double kk=a[j][i];//定义kk为第j行第i列的数 for(int k=1;k<=n+1;k++)//把每一项消成0qwq(先把第一列除了对角线全消为0然后第二第三……) // 关于处理对角线这里以i=1,j=3做例子:当k=3时,a[3][3]-=a[3][1]*a[1][3]而这个时候a[3][1]已经为0,故对对角线无影响 a[j][k]-=kk*a[i][k]; } puts("------------");//画一个杠杠来分割每一次消元结果 for(int j=1;j<=m;j++){ for(int k=1;k<=n+1;k++)cout<<a[j][k]<<" ";//输出每次消元结果 puts("");//输出空格 } } if(flag){//判断无解和多解的情况(上面已经提到了) 已经懵bi求救qwq for(int i=1;i<=m;i++) if(!check(i)){//利用check判断是无解还是多解 printf("No solution "); return 0; } //每个答案行如果有一个等于0的数就多解?? printf("So many solutions "); } }
东西又丢了!!!
补题:
#include<iostream> #include<algorithm> #include<cstdio> #include<cstring> #include<cmath> #include<cstdlib> using namespace std; long long read(){ long long ans=0; char last=' ',ch=getchar(); while(ch<'0' || ch>'9')last=ch,ch=getchar(); while(ch>='0' && ch<='9')ans=ans*10+ch-'0',ch=getchar(); if(last=='-')ans=-ans; return ans; } int n,m; double a[100][100]; int main(){ n=read(); for(int i=1;i<=n;i++) for(int j=1;j<=n+1;j++)a[i][j]=read(); int flag=0; for(int i=1;i<=n;i++){ int t=i; while(a[t][i]==0 && t<=n)t+=1; if(t==n+1){ flag=1; continue; } for(int j=1;j<=n+1;j++)swap(a[i][j],a[t][j]); double kk=a[i][i]; for(int j=1;j<=n+1;j++)a[i][j]/=kk; for(int j=1;j<=n;j++) if(i!=j){ double kk=a[j][i]; for(int k=1;k<=n+1;k++) a[j][k]-=kk*a[i][k]; } } if(flag)printf("No Solution "); else {for(int i=1;i<=n;i++) printf("%.2lf ",a[i][n+1]);} return 0; } //和上面代码差不多的,只不过这个输出的是第n+1行,也就是每一个未知数的解(因为都消成1了qwq)
行列式-定义:

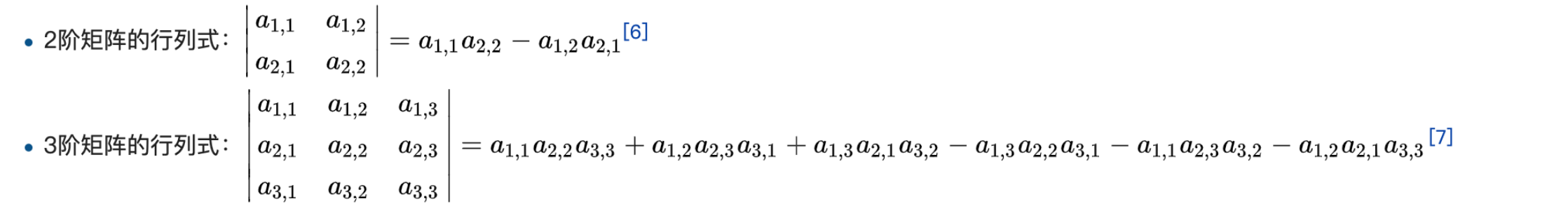
行列式计算:
1.利用高斯消元将原矩阵变为对角矩阵
2.将对角线上的值连乘得到行列式
3.同一行改变数值(数值和不变)行列式值不变
4.无解: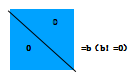
开始讲矩阵逆元了qwq:::(某位不愿透漏姓名的许姓长贵一直在催的东西qwq)
先讲定义:
逆元的定义:若矩阵B*A=I (单位矩阵I)则称B为A的左逆元(同理右逆元也可以推算)
有逆元的前提: 矩阵行列式不为0
求矩阵逆元的方法:
如何求左逆元?B*A=I A =>I 同时<=>操作 I=>B(A的逆元)【对行进行高斯消元】
如何求右逆元? A=>I
同时<=>操作 【对列进行高斯消元】
I=>B(A的逆元)
这个对行对列进行高斯消元没搞明白qwq???
看代码吧qwq(from钟神):
【问题描述】
你是能看到第一题的 friends 呢。
——hja
众所周知,小葱同学擅长计算,尤其擅长计算组合数,但这个题和组合数没什么关系。
按照规矩,大家还是练习一下,这个矩阵求逆的模板题。
给你一个N× N的矩阵A,求A在模p意义下的逆矩阵B是多少。即你要找到一个矩阵B,使得AB模p得到的结果为单位矩阵,输出任意一种解即可。
【输入格式】
第一行两个整数N, mod。
接下来N行N个数代表矩阵。
【输出格式】
输出N行N个数代表逆矩阵,保证答案一定存在。
【样例输入】
2 5
1 2
3 4
【样例输出】
3 1
4 2
【数据规模与约定】
对于10%的数据,N = 1。
对于40%的数据,N≤ 6。
对于另外20%的数据,p= 2。
对于100%的数据,1 ≤ N ≤ 100,2 ≤p≤ 109并且p为一个质数,同时读入的矩阵内的数一定在[0, p − 1],你输出的答案也需要保证这一点。
标程(不是钟神的,也不是我的qwq(懒得自己写了qwq))
#include<cstdio> #include<iostream> using namespace std; typedef long long LL; const int N=405; int mod; int n,m; LL f[N][N<<1];//与下文相照应,这里N<<1指N/2,为了构造单位矩阵而乘的2 LL r,ret; LL ksm(LL u,LL v){ ret=1; while(v){ if(v&1)ret=ret*u%mod; u=u*u%mod;v>>=1; } return ret; } int main(){ scanf("%d%d",&n,&mod);m=n*2; //乘2是为了后面建立一个单位矩阵 for(int i=1;i<=n;++i){ for(int j=1;j<=n;j++)scanf("%lld",&f[i][j]);//输入n*n的矩阵 f[i][n+i]=1; //在 f后面又搞了一个单位矩阵qwq } for(int i=1;i<=n;++i){ //高斯消元的板子 for(int j=i;j<=n;j++) if(f[j][i]){ for(int k=1;k<=m;k++) swap(f[i][k],f[j][k]); break; } if(!f[i][i]){puts("No Solution");return 0;} //判断是否有解(对角线为0) r=ksm(f[i][i],mod-2); for(int j=i;j<=m;++j) f[i][j]=f[i][j]*r%mod; for(int j=1;j<=n;++j) if(j!=i){ r=f[j][i]; for(int k=i;k<=m;++k) f[j][k]=(f[j][k]-r*f[i][k]%mod+mod)%mod; } } for(int i=1;i<=n;++i,puts("")) for(int j=n+1;j<=m;++j)printf("%lld ",f[i][j]); return 0; }
行我不想写了qwq
end-


