题目描述
如题,已知一个数列,你需要进行下面三种操作:
1.将某区间每一个数乘上x
2.将某区间每一个数加上x
3.求出某区间每一个数的和
输入输出格式
输入格式:
第一行包含三个整数N、M、P,分别表示该数列数字的个数、操作的总个数和模数。
第二行包含N个用空格分隔的整数,其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3或4个整数,表示一个操作,具体如下:
操作1: 格式:1 x y k 含义:将区间[x,y]内每个数乘上k
操作2: 格式:2 x y k 含义:将区间[x,y]内每个数加上k
操作3: 格式:3 x y 含义:输出区间[x,y]内每个数的和对P取模所得的结果
输出格式:
输出包含若干行整数,即为所有操作3的结果。
输入输出样例
说明
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=8,M<=10
对于70%的数据:N<=1000,M<=10000
对于100%的数据:N<=100000,M<=100000
(数据已经过加强^_^)
样例说明:
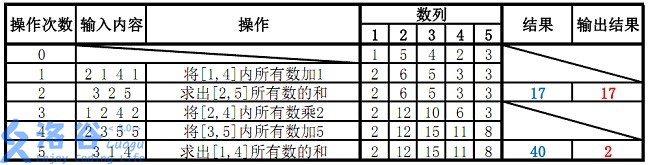
故输出应为17、2(40 mod 38=2)
好久没有写过博客了,快noip了,又上机房来做题目,不过这次上来是来做模板题的qwq
很久没有打过代码了,打起来生疏了不少呀。。。
我们来看看这道题目
这道题目要求我们区间乘法,区间加法和区间求和
我们首先来考虑加法和乘法怎么“兼容”
我们可以用两个lazytag,这里用mark[].mul表示乘,mark[].add表示加
我们可以默认乘法优先,
每次乘的时候,连mark[].add也一起乘,因为加法的lazytag可能还没有下放,如果只修改mark[].mul,我们默认的乘法优先就会出现错误
每次加的时候,只要修改mark[].add就可以了
pushdown的时候我们就
tree[v<<1]=(tree[v<<1]*mark[v].mul+(mid-l+1)*mark[v].add)%p
tree[v<<1|1]=(tree[v<<1|1]*mark[v].mul+(r-mid)*mark[v].add)%p
再维护一下lazytag就可以了

1 #include<bits/stdc++.h> 2 #define N 100005 3 #define ll long long 4 using namespace std; 5 int n,m,p,s,x,y,k; 6 int a[N]; 7 ll tree[4*N]; 8 struct node{ 9 ll add,mul; 10 }mark[4*N]; 11 void update(int v){ 12 tree[v]=(tree[v<<1]+tree[v<<1|1])%p; 13 } 14 void pushdown(int v,int l,int mid,int r){ 15 if (mark[v].mul!=1){ 16 (mark[v<<1].mul*=mark[v].mul)%=p; 17 (mark[v<<1|1].mul*=mark[v].mul)%=p; 18 (mark[v<<1].add*=mark[v].mul)%=p; 19 (mark[v<<1|1].add*=mark[v].mul)%=p; 20 (tree[v<<1]*=mark[v].mul)%=p; 21 (tree[v<<1|1]*=mark[v].mul)%=p; 22 mark[v].mul=1; 23 } 24 if (mark[v].add){ 25 (mark[v<<1].add+=mark[v].add)%=p; 26 (mark[v<<1|1].add+=mark[v].add)%=p; 27 (tree[v<<1]+=mark[v].add*(mid-l+1))%=p; 28 (tree[v<<1|1]+=mark[v].add*(r-mid))%=p; 29 mark[v].add=0; 30 } 31 } 32 void build(int v,int l,int r){ 33 mark[v].mul=1; 34 mark[v].add=0; 35 if (l==r){ 36 tree[v]=a[l]; 37 return; 38 } 39 int mid=(l+r)>>1; 40 build(v<<1,l,mid); 41 build(v<<1|1,mid+1,r); 42 update(v); 43 } 44 void mul(int v,int l,int r,int x,int y,int k){ 45 if (x<=l&&y>=r){ 46 (mark[v].mul*=k)%=p; 47 (mark[v].add*=k)%=p; 48 (tree[v]*=k)%=p; 49 return; 50 } 51 int mid=(l+r)>>1; 52 pushdown(v,l,mid,r); 53 if (y<=mid) mul(v<<1,l,mid,x,y,k); else 54 if (x>mid) mul(v<<1|1,mid+1,r,x,y,k); else 55 mul(v<<1,l,mid,x,mid,k),mul(v<<1|1,mid+1,r,mid+1,y,k); 56 update(v); 57 } 58 void add(int v,int l,int r,int x,int y,int k){ 59 if (x<=l&&y>=r){ 60 (mark[v].add+=k)%=p; 61 (tree[v]+=(ll)(r-l+1)*k)%=p; 62 return; 63 } 64 int mid=(l+r)>>1; 65 pushdown(v,l,mid,r); 66 if (y<=mid) add(v<<1,l,mid,x,y,k); else 67 if (x>mid) add(v<<1|1,mid+1,r,x,y,k); else 68 add(v<<1,l,mid,x,mid,k),add(v<<1|1,mid+1,r,mid+1,y,k); 69 update(v); 70 } 71 ll query(int v,int l,int r,int x,int y){ 72 if (x<=l&&y>=r) return tree[v]; 73 int mid=(l+r)>>1; 74 pushdown(v,l,mid,r); 75 if (y<=mid) return query(v<<1,l,mid,x,y); else 76 if (x>mid) return query(v<<1|1,mid+1,r,x,y); else 77 return (query(v<<1,l,mid,x,mid)+query(v<<1|1,mid+1,r,mid+1,y))%p; 78 } 79 int main(){ 80 scanf("%d%d%d",&n,&m,&p); 81 for (int i=1;i<=n;i++) 82 scanf("%d",&a[i]),a[i]%=p; 83 build(1,1,n); 84 for (int i=1;i<=m;i++){ 85 scanf("%d%d%d",&s,&x,&y); 86 if (s==1){ 87 scanf("%d",&k); 88 mul(1,1,n,x,y,k); 89 } else 90 if (s==2){ 91 scanf("%d",&k); 92 add(1,1,n,x,y,k); 93 } else 94 printf("%lld ",query(1,1,n,x,y)); 95 } 96 return 0; 97 }
