UVA 11168 Airport（凸包+直线方程）

题意:给你n[1,10000]个点，求出一条直线，让所有的点都在都在直线的一侧并且到直线的距离总和最小，输出最小平均值（最小值除以点数）

题解：根据题意可以知道任意角度画一条直线（所有点都在一边），然后平移去过某个点，再根据此点进行旋转直到过另一个点，这样直线就被两个点确定了

而这样的直线一定是这些点形成的凸包的边，接着就是求出凸包后枚举每条凸包的边，再根据这条边找到所有点到这条边的距离总和

但是直接找会超时，那么我们用方程优化：

已知直线上的两点P1(X1,Y1) P2(X2,Y2)， P1 P2两点不重合。

对于直线一般式：AX+BY+C=0：

A = Y2 - Y1

B = X1 - X2

C = X2*Y1 - X1*Y2

在平面直角坐标系中，已知点P（x0,y0），直线l：Ax+By+C=0(A﹒B≠0).设点P（x0,y0）到直线l的距离为d，则d=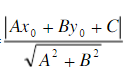

这样预处理所有x0，y0的和，就可以使用O（1）找到所有点到这条边的距离总和

还有注意n=1与n=2的情况

#include<set>
#include<map>
#include<queue>
#include<stack>
#include<cmath>
#include<vector>
#include<string>
#include<cstdio>
#include<cstring>
#include<iomanip>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;
#define eps 1E-8
/*注意可能会有输出-0.000*/
#define sgn(x) (x<-eps? -1 :x<eps? 0:1)//x为两个浮点数差的比较,注意返回整型
#define cvs(x) (x > 0.0 ? x+eps : x-eps)//浮点数转化
#define zero(x) (((x)>0?(x):-(x))<eps)//判断是否等于0
#define mul(a,b) (a<<b)
#define dir(a,b) (a>>b)
typedef long long ll;
typedef unsigned long long ull;
const int Inf=1<<28;
const ll INF=1ll<<60;
const double Pi=acos(-1.0);
const int Mod=1e9+7;
const int Max=10010;
struct Point
{
    double x,y;
    Point(double x=0,double y=0):x(x),y(y) {};
    int read()
    {
        scanf("%lf%lf",&x,&y);
    }
    inline Point operator+(const Point& a)const
    {
        return Point(x+a.x,y+a.y);
    }
    inline Point operator-(const Point& a)const
    {
        return Point(x-a.x,y-a.y);
    }
    inline bool operator<(const Point& a)const
    {
        return (sgn(x-a.x)<0||(zero(x-a.x)&&sgn(y-a.y)<0));
    }
};
typedef Point Vector;
double Cross(Vector A,Vector B)
{
    return A.x*B.y-A.y*B.x;
}
int ConvexHull(Point* p,int n,Point* convex)
{
    sort(p,p+n);
    int m=0;
    for(int i=0;i<n;++i)
    {
        while(m>1&&Cross(convex[m-1]-convex[m-2],p[i]-convex[m-2])<0)
            --m;
        convex[m++]=p[i];
    }
    int k=max(m,1);
    for(int i=n-1;i>=0;--i)
    {
        while(m>k&&Cross(convex[m-1]-convex[m-2],p[i]-convex[m-2])<0)
            --m;
        convex[m++]=p[i];
    }
    if(n>1)
        m--;
        return m;
}
Point home[Max],convex[Max];
double Solve(int n,double sumx,double sumy)
{
    if(n<=2)
        return 0;
    double minx=(double)INF;
    int m=ConvexHull(home,n,convex);
    double A,B,C;
    for(int i=1;i<=m;++i)
    {
        A=convex[i%m].y-convex[i-1].y;
        B=convex[i-1].x-convex[i%m].x;
        C=convex[i%m].x*convex[i-1].y-convex[i-1].x*convex[i%m].y;
        minx=min(minx,fabs((A*sumx+B*sumy+C*n)/(sqrt(A*A+B*B))));
    }
    return minx;
}
int main()
{
    int t,n;
    int coun=0;
    double sumx,sumy;
    scanf("%d",&t);
    while(t--)
    {
        sumx=sumy=0;
        scanf("%d",&n);
        for(int i=0; i<n; ++i)
        {
            home[i].read();
            sumx+=home[i].x;
            sumy+=home[i].y;
        }
        printf("Case #%d: %.3f
",++coun,Solve(n,sumx,sumy)/n+eps);
    }
    return 0;
}