一、蚁群算法是什么?
蚁群算法是模拟蚂蚁觅食的原理,设计出的一种群集智能算法。
蚂蚁在觅食过程中能够在其经过的路径上留下一种称为信息素的物质,并在觅食过程中能够感知这种物质的强度,并指导自己行动的方向,它们总是朝着该物质强度高的方向移动,这就形成一种类似正反馈的机制,这样经过一段时间后,整个蚁群就会沿着最短路径到达食物源了。
受到蚁群觅食的启发,于20世纪90年代意大利学者Dorigo、Maniezzo等人首先提出了蚁群系统。他们对其进行了研究,成功的使用蚁群算法解决了旅行商问题(TSP问题)。
二、图着色问题
图着色问题(Graph Coloring Problem)最早起源于“四色猜想”。19世纪英国的一位数学家提出了地图着色问题,这个问题他没能解决,不过当时的一位青年科学家提出使用四种颜色就可给地图着色,并且该地图相邻的区域所着的颜色不同,不过他没给出证明,这就是后来所说的“四色猜想”。虽然没有科学的理论来证明“四色猜想”,但是大多数人认为“四色猜想”是正确的,即对于一个平面,能仅用四种颜色就能对其进行着色,并且使得相邻部分颜色不相同。
图着色问题中所说的图一般是指数据结构中的图,由顶点和连接顶点的边构成。
虽说图着色问题看着挺简单的,看起来只要一遍遍的遍历就完事了,但是随着图的顶点的增加,时间花销越来越高,十分影响性能。所以研究该问题的人想出一系列如贪心算法、禁忌搜索算法、模拟退火算法、遗传算法、DNA 算法、蚁群算法这样高效的算法用来解决图着色问题。在图的遍历时,发现对顶点的遍历顺序其实是对结果有影响的。
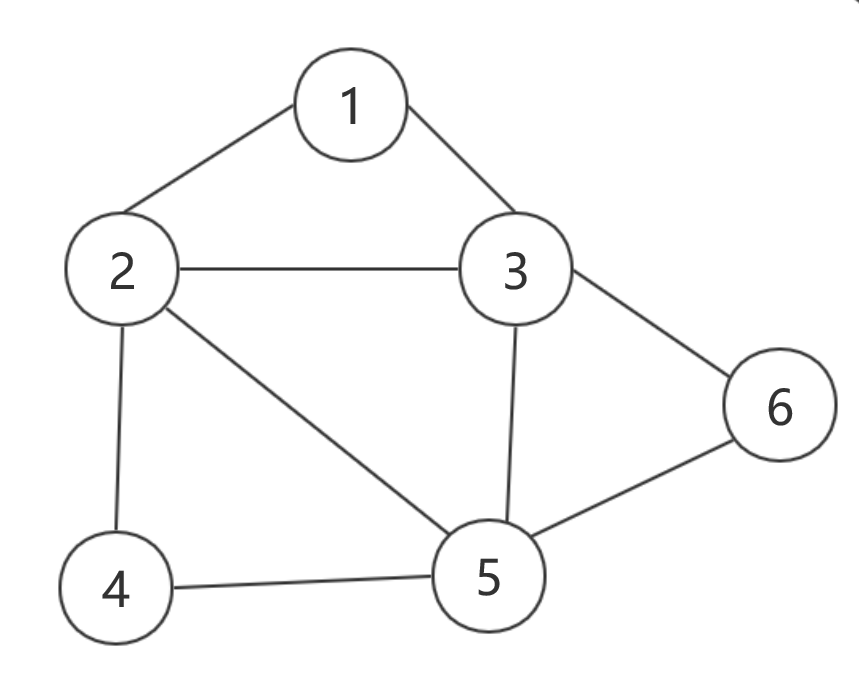
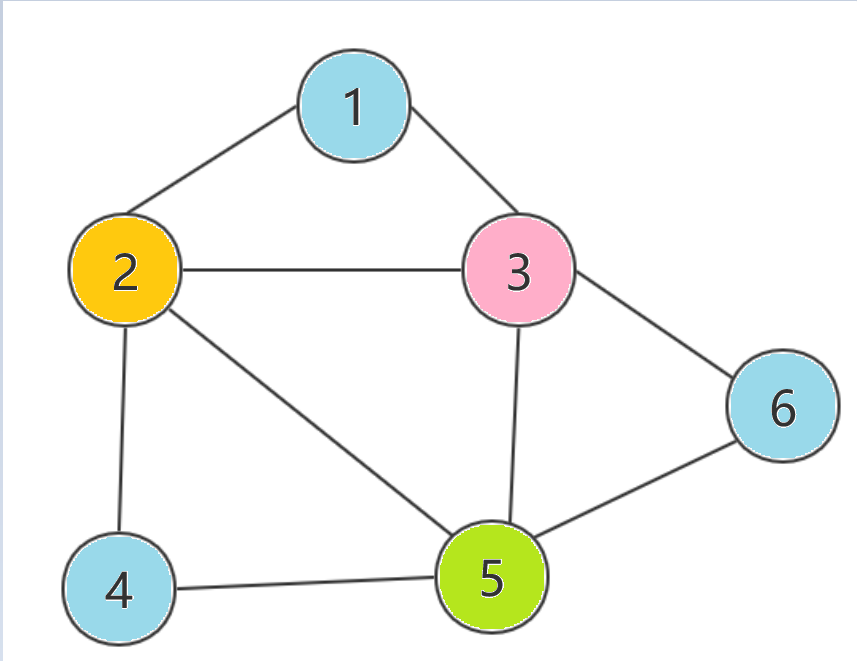
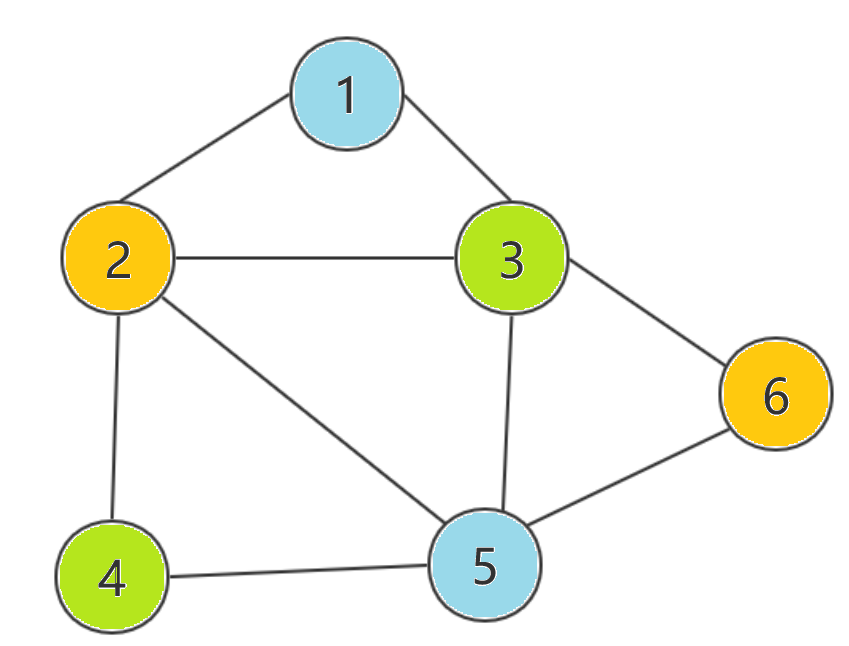
对于上图,如果着色时按照一定顺序遍历每个顶点,每到达一个新顶点,就遍历以前用过的颜色,直到新顶点上色后与相邻顶点颜色不冲突,如果已有的每种颜色都与相邻顶点颜色冲突,则用一种新的颜色。如果顶点顺序为1->2->4->5->3->6,着色将会变成中间那幅图的样子,使用了四种颜色。而如果着色顺序变成2->1->3->6->5->4,那就只用了三种颜色。而蚁群算法能够通过蚁群的协同作用来找到最佳路径为图着色问题提出解决方案。
三、蚁群算法使用在图着色问题上的步骤
步骤 1:对蚁群算法中的各个参数进行初始化。构造出图G的邻接矩阵为着色做准备。
步骤 2:让所有的人工蚂蚁从图的第一个顶点出发,开始遍历。
步骤 3:人工蚂蚁开始给所经过的顶点着色。开始遍历时着色的颜色集为空, 则使用第一种颜色为第一个顶点进行着色。
步骤 4:在人工蚂蚁需要向邻近的结点进行转移时,需要计算这些人工蚂蚁向邻近的结点转移的概率,并且确定人工蚂蚁前进的方向。人工蚂蚁在结点 i 向另一个结点 j 转移的概率公式为:

其中 ŋij表示启发式信息,ŋij=1/Numc,其中Numc 表示 vi-1 着色后使用的总颜色数。Τ(i,j)表示在顶点 i 向顶点 j 转移时留下的信息素的量。 在人工蚂蚁向邻近结点转移后需要对路径上的信息素进行更新信息素的 更新公式为:
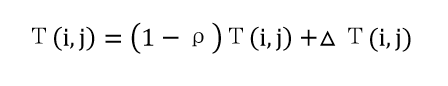
其中:
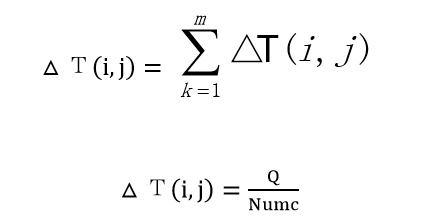
公式中 Q 表示路径上信息素的强度,Numc 表示给上一个顶点着色后使用的 颜色数。
步骤 5:给人工蚂蚁所在的顶点进行着色,使用颜色集合中的颜色试探性给该顶点进行着色,若产生冲突则换用下一种颜色,如果颜色集中所有颜色都不能给该顶点进行着色,则使用一种 新的颜色给该顶点进行着色。
步骤 6:判断是否完成了所有的顶点着色,若没有则转到步骤 3,否则表示该人工蚂蚁完成了一次的着色过程。
步骤 7:判断是否达到了最大的迭代次数,若是,则表示蚁群算法运行结束, 并输出最优的着色结果,否则转到步骤 2 开始下一次的迭代过程。