题目链接:http://www.lydsy.com/JudgeOnline/problem.php?id=2820
题意:多次询问,求1<=x<=N, 1<=y<=M且gcd(x,y)为质数有多少对。
首先, 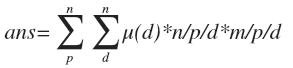
由于这里是多次询问,并且数据很大,显然不能直接求解,需要做如下处理。。
整数的除法是满足结合律的,然后我们设T=p*d,有:
注意到后面部分是可以预处理出来的,那么整个ans就可以用分块处理来求了,设
那么有 ,考虑当p|x时,根据莫比菲斯mu(x)的性质,px除以其它非p的质数因数都为0,所以g(px)=mu(x)。当p!|x时,除数为p时为mu(x),否则其它的和为-g(x),因为这里还乘了一个p所以要变反。然后O(n)预处理下就可以了。。
,考虑当p|x时,根据莫比菲斯mu(x)的性质,px除以其它非p的质数因数都为0,所以g(px)=mu(x)。当p!|x时,除数为p时为mu(x),否则其它的和为-g(x),因为这里还乘了一个p所以要变反。然后O(n)预处理下就可以了。。
1 //STATUS:C++_AC_3660MS_274708KB 2 #include <functional> 3 #include <algorithm> 4 #include <iostream> 5 //#include <ext/rope> 6 #include <fstream> 7 #include <sstream> 8 #include <iomanip> 9 #include <numeric> 10 #include <cstring> 11 #include <cassert> 12 #include <cstdio> 13 #include <string> 14 #include <vector> 15 #include <bitset> 16 #include <queue> 17 #include <stack> 18 #include <cmath> 19 #include <ctime> 20 #include <list> 21 #include <set> 22 //#include <map> 23 using namespace std; 24 //#pragma comment(linker,"/STACK:102400000,102400000") 25 //using namespace __gnu_cxx; 26 //define 27 #define pii pair<int,int> 28 #define mem(a,b) memset(a,b,sizeof(a)) 29 #define lson l,mid,rt<<1 30 #define rson mid+1,r,rt<<1|1 31 #define PI acos(-1.0) 32 //typedef 33 typedef long long LL; 34 typedef unsigned long long ULL; 35 //const 36 const int N=10000010; 37 const int INF=0x3f3f3f3f; 38 const int MOD=100000,STA=8000010; 39 const LL LNF=1LL<<60; 40 const double EPS=1e-8; 41 const double OO=1e15; 42 const int dx[4]={-1,0,1,0}; 43 const int dy[4]={0,1,0,-1}; 44 const int day[13]={0,31,28,31,30,31,30,31,31,30,31,30,31}; 45 //Daily Use ... 46 inline int sign(double x){return (x>EPS)-(x<-EPS);} 47 template<class T> T gcd(T a,T b){return b?gcd(b,a%b):a;} 48 template<class T> T lcm(T a,T b){return a/gcd(a,b)*b;} 49 template<class T> inline T lcm(T a,T b,T d){return a/d*b;} 50 template<class T> inline T Min(T a,T b){return a<b?a:b;} 51 template<class T> inline T Max(T a,T b){return a>b?a:b;} 52 template<class T> inline T Min(T a,T b,T c){return min(min(a, b),c);} 53 template<class T> inline T Max(T a,T b,T c){return max(max(a, b),c);} 54 template<class T> inline T Min(T a,T b,T c,T d){return min(min(a, b),min(c,d));} 55 template<class T> inline T Max(T a,T b,T c,T d){return max(max(a, b),max(c,d));} 56 //End 57 58 LL sum[N],g[N]; 59 int isprime[N],mu[N],prime[N]; 60 int cnt; 61 int T,n,m; 62 63 void Mobius(int n) 64 { 65 int i,j; 66 //Init isprime[N],mu[N],prime[N],全局变量初始为0 67 cnt=0;mu[1]=1; 68 for(i=2;i<=n;i++){ 69 if(!isprime[i]){ 70 prime[cnt++]=i; 71 mu[i]=-1; 72 g[i]=1; 73 } 74 for(j=0;j<cnt && i*prime[j]<=n;j++){ 75 isprime[i*prime[j]]=1; 76 if(i%prime[j]){ 77 mu[i*prime[j]]=-mu[i]; 78 g[i*prime[j]]=mu[i]-g[i]; 79 } 80 else { 81 mu[i*prime[j]]=0; 82 g[i*prime[j]]=mu[i]; 83 break; 84 } 85 } 86 } 87 for(i=1;i<=n;i++)sum[i]=sum[i-1]+g[i]; 88 } 89 90 int main(){ 91 // freopen("in.txt","r",stdin); 92 int i,j,la; 93 LL ans; 94 Mobius(10000000); 95 scanf("%d",&T); 96 while(T--) 97 { 98 scanf("%d%d",&n,&m); 99 100 if(n>m)swap(n,m); 101 ans=0; 102 for(i=1;i<=n;i=la+1){ 103 la=Min(n/(n/i),m/(m/i)); 104 ans+=(sum[la]-sum[i-1])*(n/i)*(m/i); 105 } 106 107 printf("%lld ",ans); 108 } 109 return 0; 110 }