二分和三分
标签(空格分隔): @zhshh cpp OI
二分问题
模板
离散二分答案
int check (int x){
//检查x是否符合,符合 真,不符合 假
}
int search (int l,int r){
int mid;
while(l<=r){
mid=(l+r)/2;
if(check(mid)){
l=mid+1;
ans=mid;
}else{
r=mid-1;
}
}
return ans;
}
可以看到,假定一个(x)充分小,可以使得(check(x))成立,那么明显,在(search(l,r))中,存在(x_0)使得(x in [l,x_0],check(x)=true),(x in (x_0,r],check(x)=false),注意(x_0)是从(l)开始最大的满足的值。
也就是如果改成(!check()),那么就是(check(x)=true)是从(x_{true})连续到r的,即(x in [l,x_0],!check(x)=true,xin[x_{true},r],!check(x)=false),因此二分求解的(answer)是(x_0),而最小成立值(x_{true}=x_0+1),因此返回时要return ans+1下面代码。
int check (int x){
//检查x是否符合,符合 真,不符合 假
}
int search (int l,int r){
int mid;
while(l<=r){
mid=(l+r)/2;
if(!check(mid)){
l=mid+1;
ans=mid;
}else{
r=mid-1;
}
}
return ans+1;
}
连续二分答案
很简单的二分,边界条件也不需要十分注意。最后return时,无论是left,right还是mid都可以,因为(mid=(left+right)/2)而此时mid,left,right,都是比较接近(最大差值eps)的。
#define eps 1e-6
int check (int x){
//检查x是否符合,符合:真,不符合:假。
}
double search(){
double mid;
while(fabs(left-right)>eps){
mid=(left+right)/2;
if(check(mid)){
right=mid;
}else{
left=mid;
}
}
return left;
}
离散二分查找
转载自你真的会写二分查找吗 By luoxn28
下面的都是针对直接sort后的不严格单调递增的序列
下面六种本质区别就是一个恰当的check函数
1 查找第一个与key相等的元素
查找第一个相等的元素,也就是说等于查找key值的元素有好多个,返回这些元素最左边的元素下标。
// 查找第一个相等的元素
static int findFirstEqual(int[] array, int key) {
int left = 0;
int right = array.length - 1;
// 这里必须是 <=
while (left <= right) {
int mid = (left + right) / 2;
if (array[mid] >= key) {
right = mid - 1;
}
else {
left = mid + 1;
}
}
if (left < array.length && array[left] == key) {
return left;
}
return -1;
}
2 查找最后一个与key相等的元素
查找最后一个相等的元素,也就是说等于查找key值的元素有好多个,返回这些元素最右边的元素下标。
// 查找最后一个相等的元素
static int findLastEqual(int[] array, int key) {
int left = 0;
int right = array.length - 1;
// 这里必须是 <=
while (left <= right) {
int mid = (left + right) / 2;
if (array[mid] <= key) {
left = mid + 1;
}
else {
right = mid - 1;
}
}
if (right >= 0 && array[right] == key) {
return right;
}
return -1;
}
3 查找最后一个等于或者小于key的元素
查找最后一个等于或者小于key的元素,也就是说等于查找key值的元素有好多个,返回这些元素最右边的元素下标;如果没有等于key值的元素,则返回小于key的最右边元素下标。
// 查找最后一个等于或者小于key的元素
static int findLastEqualSmaller(int[] array, int key) {
int left = 0;
int right = array.length - 1;
// 这里必须是 <=
while (left <= right) {
int mid = (left + right) / 2;
if (array[mid] > key) {
right = mid - 1;
}
else {
left = mid + 1;
}
}
return right;
}
4 查找最后一个小于key的元素
查找最后一个小于key的元素,也就是说返回小于key的最右边元素下标。
// 查找最后一个小于key的元素
static int findLastSmaller(int[] array, int key) {
int left = 0;
int right = array.length - 1;
// 这里必须是 <=
while (left <= right) {
int mid = (left + right) / 2;
if (array[mid] >= key) {
right = mid - 1;
}
else {
left = mid + 1;
}
}
return right;
}
5 查找第一个等于或者大于key的元素
查找第一个等于或者大于key的元素,也就是说等于查找key值的元素有好多个,返回这些元素最左边的元素下标;如果没有等于key值的元素,则返回大于key的最左边元素下标。
// 查找第一个等于或者大于key的元素
static int findFirstEqualLarger(int[] array, int key) {
int left = 0;
int right = array.length - 1;
// 这里必须是 <=
while (left <= right) {
int mid = (left + right) / 2;
if (array[mid] >= key) {
right = mid - 1;
}
else {
left = mid + 1;
}
}
return left;
}
6 查找第一个大于key的元素
查找第一个等于key的元素,也就是说返回大于key的最左边元素下标。
// 查找第一个大于key的元素
static int findFirstLarger(int[] array, int key) {
int left = 0;
int right = array.length - 1;
// 这里必须是 <=
while (left <= right) {
int mid = (left + right) / 2;
if (array[mid] > key) {
right = mid - 1;
}
else {
left = mid + 1;
}
}
return left;
}
7 二分查找变种总结
#include <iostream>
#include <cstdio>
#define MX 10010
using namespace std;
int a[MX];
int n;
int FindFirstEqual(int key){
int left=1;
int right=n;
while(left<=right){
int mid=(left+right)/2;
if(a[mid]>=key){
right=mid-1;
}else{
left=mid+1;
}
}
if(left<=n && a[left]==key){
return left;
}
return -1;
}
int FindLastEqual(int key){
int left=1;
int right=n;
while(left<=right){
int mid=(left+right)/2;
if(a[mid]<=key){
left=mid+1;
}else{
right=mid-1;
}
}
if(right>=1 && a[right]==key){
return right;
}
return -1;
}
int FindLastNotMore(int key){
int left=1;
int right=n;
while(left<=right){
int mid=(left+right)/2;
if(a[mid]>key){
right=mid-1;
}else{
left=mid+1;
}
}
return right;
}
int FindLastLess(int key){
int left=1;
int right=n;
while(left<=right){
int mid=(left+right)/2;
if(a[mid]>=key){
right=mid-1;
}else{
left=mid+1;
}
}
return right;
}
int FindFirstNotLess(int key){
int left=1;
int right=n;
while(left<=right){
int mid=(left+right)/2;
if(a[mid]>=key){
right=mid-1;
}else{
left=mid+1;
}
}
return left;
}
int FindFirstMore(int key){
int left=1;
int right=n;
while(left<=right){
int mid=(left+right)/2;
if(a[mid]>key){
right=mid-1;
}else{
left=mid+1;
}
}
return left;
}
void init(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
}
int main(){
freopen("a.txt","r",stdin);
// a.txt
// 15
// 1 1 2 5 5 5 5 5 5 6 7 8 9 11 13
cout<<"15
1 1 2 5 5 5 5 5 5 6 7 8 9 11 13
";
cout<<" 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
";
init();
int x=3;
cout<<"FindFirstEqual(x)"<<FindFirstEqual(x)<<endl;
cout<<"FindLastEqual(x)"<<FindLastEqual(x)<<endl;
cout<<"FindFirstMore(x)"<<FindFirstMore(x)<<endl;
cout<<"FindFirstNotLess(x)"<<FindFirstNotLess(x)<<endl;
cout<<"FindLastNotMore(x)"<<FindLastNotMore(x)<<endl;
cout<<"FindLastLess(x)"<<FindLastLess(x)<<endl;
}
8 上面六种方法汇总
// 这里必须是 <=
while (left <= right) {
int mid = (left + right) / 2;
if (array[mid] ? key) {
//... right = mid - 1;
}
else {
// ... left = mid + 1;
}
}
return xxx;
int xxx(int key){
int left=1;
int right=n;
while(left<=right){
int mid=(left+right)/2;
if(a[mid]>=key){
right=mid-1;
}else{
left=mid+1;
}
}
...
return xxx
}
三分问题
可以认为三分求导极值--二分零点
离散型
/型
int SanFen(int l,int r) //找凸点
{
while(l < r-1)
{
int mid = (l+r)/2;
int mmid = (mid+r)/2;
if( f(mid) > f(mmid) )
r = mmid;
else
l = mid;
}
return f(l) > f(r) ? l : r;
}
/型
int SanFen(int l,int r) //找凸点
{
while(l < r-1)
{
int mid = (l+r)/2;
int mmid = (mid+r)/2;
if( f(mid) > f(mmid) )
l = mid;
else
r = mmid;
}
return f(l) > f(r) ? l : r;
}
连续型
/型
double three_devide(double low,double up)
{
double m1,m2;
while(up-low>=eps)
{
m1=low+(up-low)/3;
m2=up-(up-low)/3;
if(f(m1)<=f(m2))
low=m1;
else
up=m2;
}
return (m1+m2)/2;
}
/型
double three_devide(double low,double up)
{
double m1,m2;
while(up-low>=eps)
{
m1=low+(up-low)/3;
m2=up-(up-low)/3;
if(f(m1)<=f(m2))
up=m2;
else
low=m1;
}
return (m1+m2)/2;
}
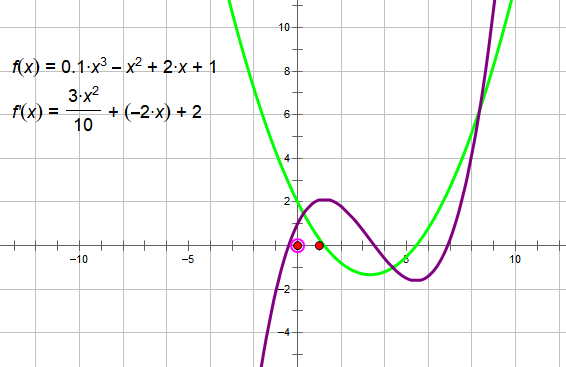
应用
#include <iostream>
using namespace std;
double f(double x){
return (0.1*x*x*x-x*x+2*x+1);
}
double sanfenshangtu(double left,double right){
double m1,m2;
double eps=1e-8;
while(right-left>=eps){
m1=left+(right-left)/3;
m2=right-(right-left)/3;
if(f(m1)>f(m2)){
right=m2;
}else{
left=m1;
}
}
return (left+right)/2;
}
double sanfenxiatu(double left,double right){
double m1,m2;
double eps=1e-8;
while(right-left>=eps){
m1=left+(right-left)/3;
m2=right-(right-left)/3;
if(f(m1)<f(m2)){
right=m2;
}else{
left=m1;
}
}
return (left+right)/2;
}
int main(){
cout<<sanfenshangtu(0,10)<<endl<<f(sanfenshangtu(0,10))<<endl;
cout<<sanfenxiatu(0,10)<<endl<<f(sanfenxiatu(0,10))<<endl;
}

[Running] cd "o:2" && g++ sanfen.cpp -o sanfen && "o:2"sanfen
1.22515
2.1332
5.44152
-1.61468
[Done] exited with code=0 in 0.487 seconds