原文链接http://www.cnblogs.com/zhouzhendong/p/9055728.html
题目传送门 - Codeforces 928E
题意
一束与坐标轴平行或者成$45^circ$角的光线在一个矩形区域内反射。
如图:
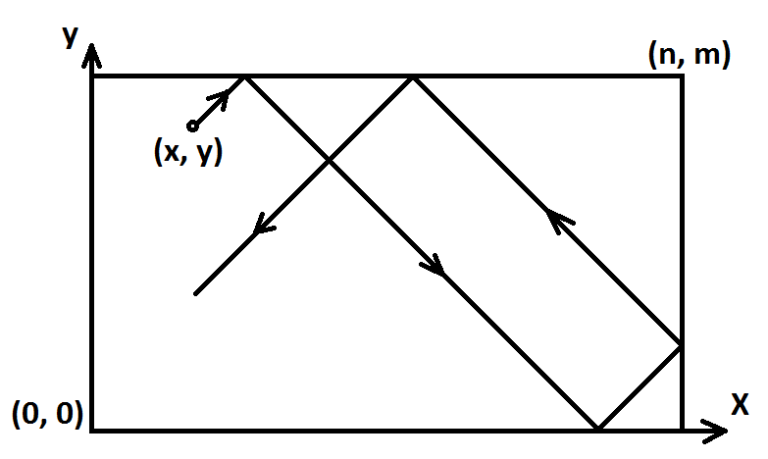
给定矩形的长宽,以及光源位置、光线初始方向,问它最先到达四个角落中的哪一个角落。如果永远不能到达,输出$-1$。
题解
本来不想写的。本次CF又打烂了。
D题一个傻逼错误调了40多分钟。
E题貌似挺可做的。可是来不及啊。(再加上深更半夜神志不清)
我们来回顾一下初中数学套路。
考虑将每次反射做一个对称。
我来画一下一组数据:
5 3 4 0 1 1

通过对称,我们把它画成这样(经典初中数学套路):
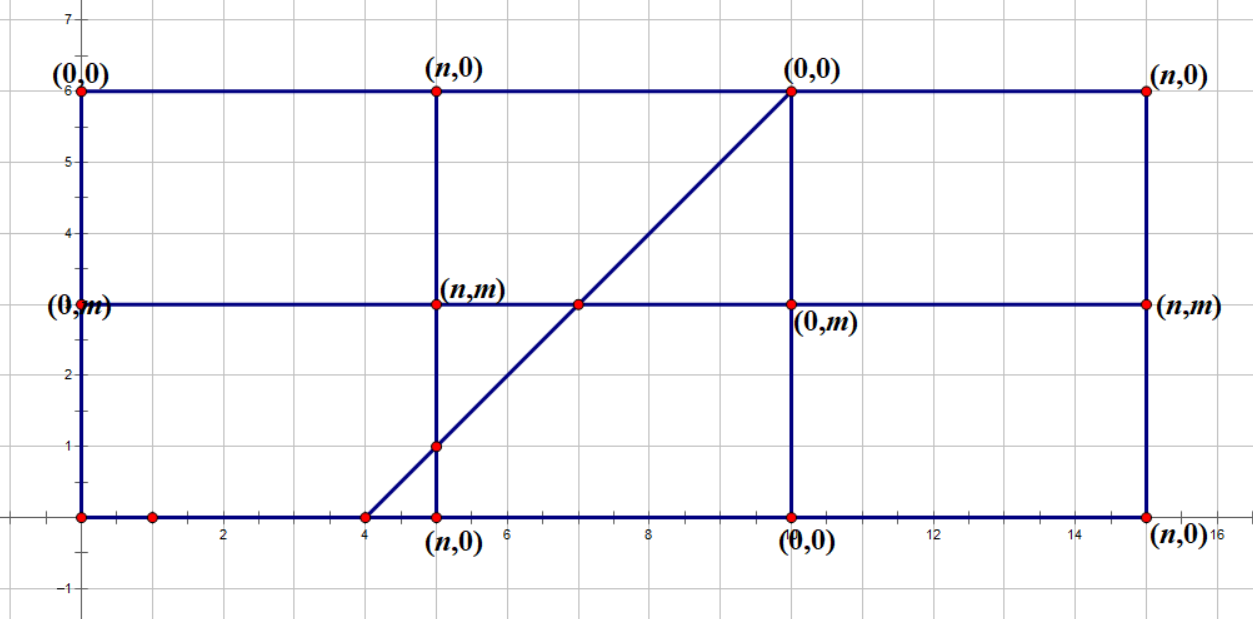
然后问题就大致变成了求直线到达的第一个满足$n|T_x,m|T_y$的点$(T_x,T_y)$。
为了方便,我们再把原图画成这样:

问题进一步简化,变成从$s'$出发的问题了。
设$S=(x,y)$,则$S'=(0,y-x)$,
不难列出方程:
$an+(y-x)=bm Longrightarrow an+bm=(x-y)$
然后我们用exgcd来解一下这个方程,首先判掉无解的情况,输出$-1$。
然后注意一下我们要求的是第一个碰到的这样的点,所以在特殊情况的时候要小心。
要取$a$的尽量小的正整数值。我一开始写错了,对$m$取模,然后突然发现应该对$m/gcd(n,m)$取模……
然后根据算出来的$a$以及$b$的奇偶性来确定到达的位置。
至于一开始输入的:
如果是平行坐标轴的,那么直接判掉。
如果是$45^circ$的,那么我们可以通过在原矩形中取对称来使其变成我们需要的那样。
题外话:
又错失一次上黄的机会QAQ。
话说我的代码跑的挺快的。
话说为什么目前我$friends$里面的三位大佬(xza,bestfy,emoairx)的代码怎么都要跑几百$MS$……后来才发现他们的那个循环好像不是$O(1)$的……
QAQ大佬都会写循环……只有我这种菜鸡才去写公式。关键是还写挂了调了有一会儿……(就是之前提到过的那个问题)
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
int n,m,x,y,vx,vy;
int refx,refy;
LL exgcd(LL a,LL b,LL &x,LL &y){
if (!b){
x=1,y=0;
return a;
}
LL res=exgcd(b,a%b,y,x);
y-=(a/b)*x;
return res;
}
int main(){
scanf("%d%d%d%d%d%d",&n,&m,&x,&y,&vx,&vy);
if (vx==0){
if (x==0||x==n){
if (vy==1)
printf("%d %d
",x,m);
else
printf("%d %d
",x,0);
}
else
puts("-1");
return 0;
}
if (vy==0){
if (y==0||y==m){
if (vx==1)
printf("%d %d
",n,y);
else
printf("%d %d
",0,y);
}
else
puts("-1");
return 0;
}
if (vx==-1)
refx=1,x=n-x;
if (vy==-1)
refy=1,y=m-y;
//s'=(0,y-x)
//an+(y-x)=bm => an+bm=(x-y)
LL a,b,g;
g=exgcd(n,m,a,b);
if ((x-y)%g!=0){
puts("-1");
return 0;
}
LL t=(x-y)/g;
a*=t,b*=t;
int _m=m/g,_n=n/g;
LL _a=(a%_m+_m+_m-1)%_m+1,_b=-((x-y)-_a*n)/m;
LL ansx=n,ansy=m;
if (_a%2==0)
ansx=n-ansx;
if (_b%2==0)
ansy=m-ansy;
if (refx)
ansx=n-ansx;
if (refy)
ansy=m-ansy;
printf("%I64d %I64d",ansx,ansy);
return 0;
}