欢迎访问~原文出处——博客园-zhouzhendong
去博客园看该题解
题目传送门 - BZOJ3772
题意概括
给出一个树,共n个节点。
有m条互不相同的树上路径。
现在让你随机选择2条路径,问两条路径存在包含关系的概率(输出最简分数)。
n,m<=100000
题解
首先,暴力肯定过不去的。
然后,我们发现总选择的方案数是C(m,2)
然后重点是统计包含关系的。
现在,我们有一个做法。
我们先把整个树的dfs序搞出来。
然后,相当于某一个子树就是连续的一段。对于输入的每一个路径(x,y),我们在x处打一个y标记,在y处打一个x标记。然后比如我们要搜寻包含路径(a,b)的路径,那么只需要在保证其他的x,y分别处于ab两侧,我们只需要统计在a一侧的标记在b一侧有多少对应的标记即可。
于是我们用到了主席树。(你要写线段树套线段树我也不拦你)。
主席树的时间和区间各表示一种标记。
比如在路径(x,y),那么就在时间x的时候区间[y,y]加1。
如果不大懂可以参见其他大佬的博客。
标记打好之后是关键部分。
对于每一条路径(a,b),我们分类讨论。
设LCA(a,b)=c
情况1:
a≠c且b≠c:
如图:
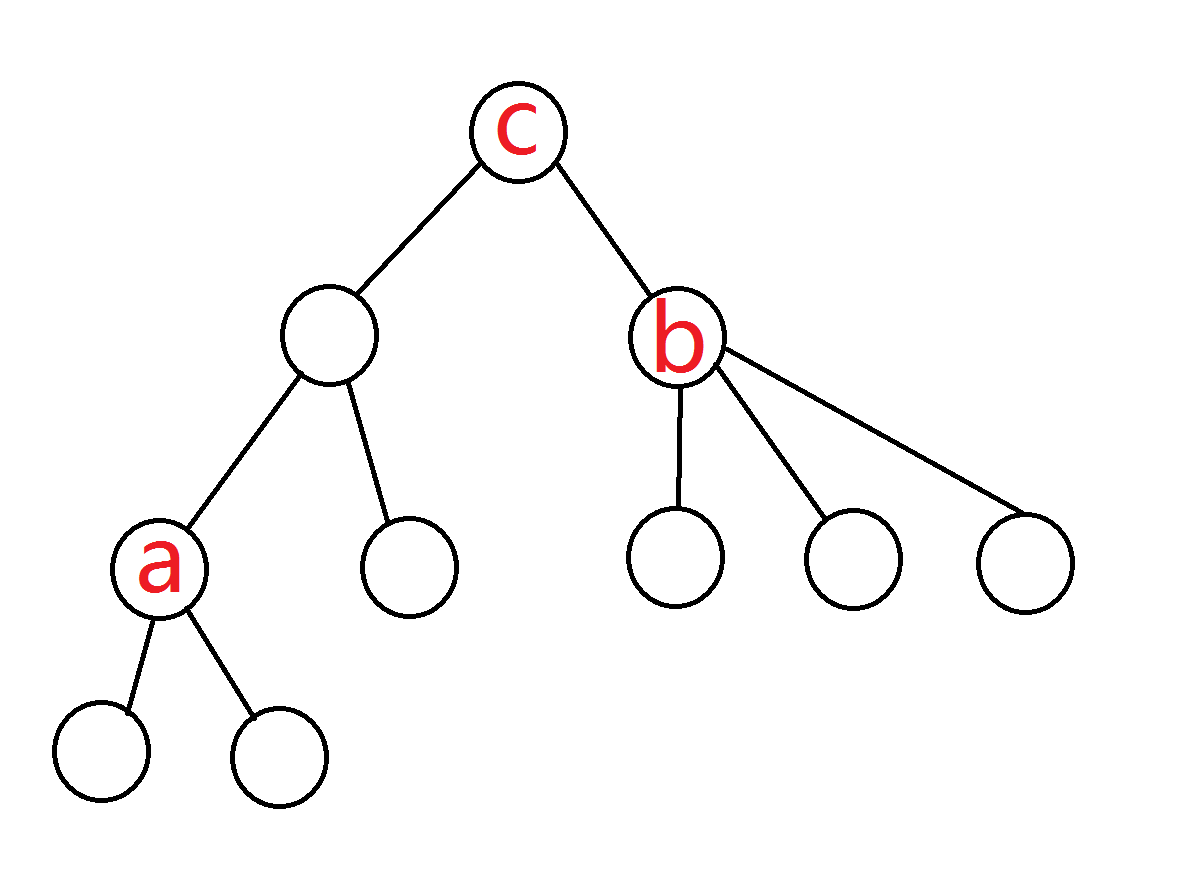
那么,只需要统计在a的子树中的节点所对应的标记在b的子树中有几个即可。别忘记减掉它本身。(-1即可)
情况2:a,b中有一个=c,不妨设b=c
如图:
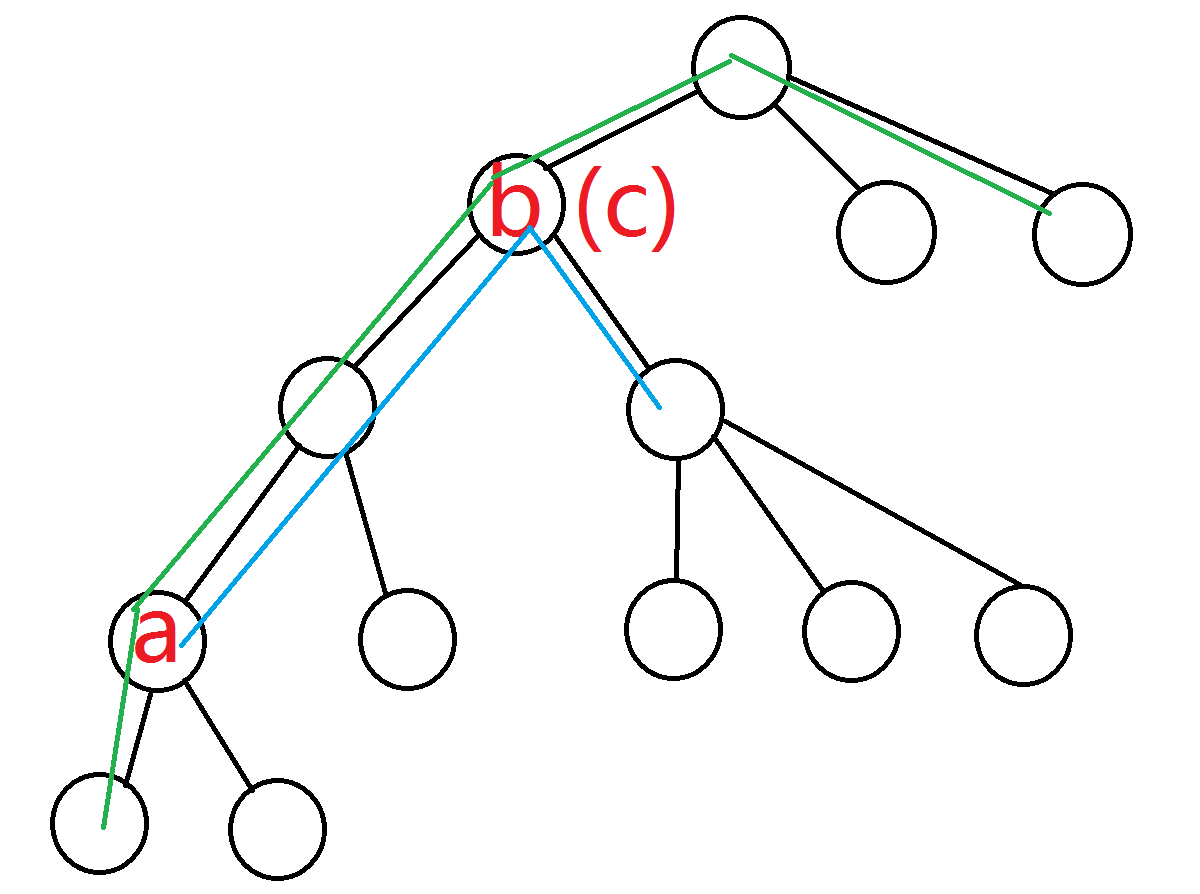
那么,我们发现,从子树a的节点出发,既要统计b的爸爸延伸出去的(绿色路径),又要统计b除了到a路径上的儿子以外的其他儿子的(如蓝色路径),貌似很麻烦。
实际上,就是全局的减去b到a路径上的b的儿子的。至于这个儿子,倍增就可以求了。别忘了-1。
情况3:a=b=c
这个很明显就是就a的子树节点出发,统计全局除了a子树的答案。
一切的一切,主席树统统搞定。
最后,提供一组数据:
11 7
1 2
1 3
1 8
2 4
2 5
3 6
3 7
3 11
6 9
6 10
2 2
4 8
2 1
3 2
3 10
9 10
9 11
ans=5/21
代码
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstdlib>
#include <vector>
using namespace std;
typedef long long LL;
LL gcd(LL a,LL b){return b?gcd(b,a%b):a;}
const int N=100005;
struct Gragh{
int cnt,y[N*2],nxt[N*2],fst[N];
void clear(){
cnt=0;
memset(fst,0,sizeof fst);
}
void add(int a,int b){
y[++cnt]=b,nxt[cnt]=fst[a],fst[a]=cnt;
}
}g;
int n,m,time;
int dfn[N],in[N],out[N],fa[N][20],depth[N];
vector <int> v[N];
struct Que{
int a,b;
}q[N];
void dfs(int rt,int pre){
depth[rt]=depth[pre]+1;
fa[rt][0]=pre;
for (int i=1;i<20;i++)
fa[rt][i]=fa[fa[rt][i-1]][i-1];
dfn[in[rt]=++time]=rt;
for (int i=g.fst[rt];i;i=g.nxt[i])
if (g.y[i]!=pre)
dfs(g.y[i],rt);
out[rt]=time;
}
bool isfa(int a,int b){
return in[a]<=in[b]&&out[b]<=out[a];
}
int LCS(int a,int b){
for (int i=19;i>=0;i--)
if (fa[a][i]&&!isfa(fa[a][i],b))
a=fa[a][i];
return a;
}
int LCA(int a,int b){
if (isfa(a,b))
return a;
if (isfa(b,a))
return b;
return fa[LCS(a,b)][0];
}
const int S=N*2*20;
int ls[S],rs[S],sum[S],total=0,root[N];
void build(int &rt,int L,int R){
rt=++total;
sum[rt]=0;
if (L==R)
return;
int mid=(L+R)>>1;
build(ls[rt],L,mid);
build(rs[rt],mid+1,R);
}
void add(int prt,int &rt,int L,int R,int pos){
if (!rt||rt==prt)
rt=++total,sum[rt]=sum[prt];
sum[rt]++;
if (L==R)
return;
if (!ls[rt])
ls[rt]=ls[prt];
if (!rs[rt])
rs[rt]=rs[prt];
int mid=(L+R)>>1;
if (pos<=mid)
add(ls[prt],ls[rt],L,mid,pos);
else
add(rs[prt],rs[rt],mid+1,R,pos);
}
int query(int prt,int rt,int L,int R,int xL,int xR){
if (xL>R||xR<L)
return 0;
if (xL<=L&&R<=xR)
return sum[rt]-sum[prt];
int mid=(L+R)>>1;
return query(ls[prt],ls[rt],L,mid,xL,xR)
+query(rs[prt],rs[rt],mid+1,R,xL,xR);
}
int main(){
g.clear();
scanf("%d%d",&n,&m);
for (int i=1,a,b;i<n;i++){
scanf("%d%d",&a,&b);
g.add(a,b);
g.add(b,a);
}
time=0;
dfs(1,0);
for (int i=1;i<=n;i++)
v[i].clear();
for (int i=1,a,b;i<=m;i++){
scanf("%d%d",&a,&b);
if (in[a]>in[b])
swap(a,b);
v[in[a]].push_back(in[b]);
v[in[b]].push_back(in[a]);
q[i].a=a,q[i].b=b;
}
build(root[0],1,n);
for (int i=1;i<=n;i++){
root[i]=root[i-1];
for (int j=0;j<v[i].size();j++)
add(root[i-1],root[i],1,n,v[i][j]);
}
LL x=0,y=1LL*m*(m-1)/2;
for (int i=1;i<=m;i++){
int a=q[i].a,b=q[i].b,c=LCA(a,b);
if (a!=c&&b!=c){
x+=query(root[in[a]-1],root[out[a]],1,n,in[b],out[b]);
x--;
}
else if (a!=c||b!=c){
if (b!=c)
swap(a,b);
int d=LCS(a,b);
x+=query(root[in[a]-1],root[out[a]],1,n,1,n);
x-=query(root[in[a]-1],root[out[a]],1,n,in[d],out[d]);
x--;
}
else {
x+=query(root[in[a]-1],root[out[a]],1,n,1,n);
x-=query(root[in[a]-1],root[out[a]],1,n,in[a],out[a]);
}
}
LL g=gcd(y,x);
x/=g,y/=g;
if (x==0)
puts("0");
else
printf("%lld/%lld
",x,y);
return 0;
}