概要
参考《大话数据结构》,把常用的基本数据结构梳理一下。
本节介绍二叉树。
定义
二叉树(Binary Tree)是 (n) ((n geqslant 0))个结点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树的二叉树组成。
二叉树的特点:
- 每个结点最多有两棵子树,所以二叉树中不存在度大于 (2) 的结点。
- 左子树和右子树是有顺序的,次序不能任意颠倒。
- 即使树中某结点只有一棵子树,也要区分它是左子树还是右子树。
所有的结点都只有左子树的二叉树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。这两者统称为斜树。
在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树。
对一棵具有 (n) 个结点的二叉树按层序编号,如果编号为 (i) ((1 leqslant i leqslant n))的结点与同样深度的满二叉树中编号为 (i) 的结点在二叉树中位置完全相同,则这棵二叉树称为完全二叉树。如图:
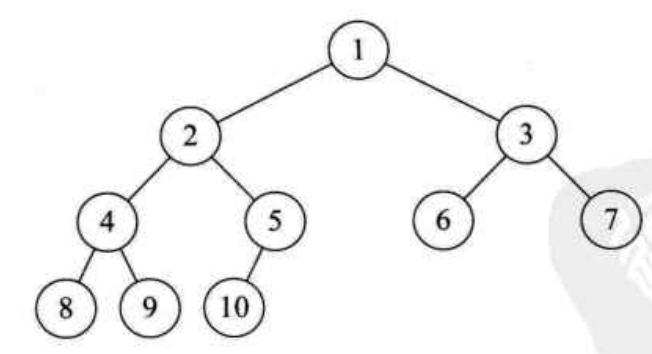
注意:首先满二叉树一定是一棵完全二叉树,但完全二叉树又不一定是满的,其次按层序编号相同的结点是一一对应的。从这里得出一些完全二叉树的特点:
- 叶子结点只能出现在最下两层
- 最下层的叶子一定集中在左部连续位置
- 倒数二层,若有叶子结点,一定都在右部连续位置
- 如果结点度为 (1),则该结点只有左孩子,即不存在只有右子树的情况
- 同样结点数的二叉树,完全二叉树的深度最小
二叉树的性质
性质 1: 在二叉树的第 (i) 层上至多有 (2^{i-1}) 个结点((i geqslant 1))。
性质 2: 深度为 (k) 的二叉树至多有 (2^k-1) 个结点((k geqslant 1))。
性质 3: 对任何一棵二叉树 (T),如果其终端结点数为 (n_0),度为 (2) 的结点数为 (n_2),则 (n_0 = n_2 +1).
说白了就是叶子结点数比度为 (2) 的结点数多一个。我们设 (n_1) 为度是 (1) 的结点数。则树 (T) 的结点总数 (n=n_0+n_1+n_2). 我们换个角度数一数树的连接线数,度为 (1) 的分支线为 (1) 条,度为 (2) 的分支线为 (2) 条,即共 (n_1+2n_2) 条,又显然树的连接树为结点总数减去 (1),即 (n-1 = n_1+ 2n_2),即 (n_0 = n_2 +1).
性质 4: 具有 (n) 个结点的完全二叉树的深度为 (floor(log_2n)+1)((floor(x)) 表示不超过 (x) 的最大整数)。
性质 5: 如果对一棵有 (n) 个结点的完全二叉树(其深度为 (floor(log_2n)+1))的结点按层序编号(从第一层到 (floor(log_2n)+1) 层,每层从左到右),对任一结点 (i)((1 leqslant i leqslant n))有:
- 如果 (i=1),则结点 (i) 是二叉树的根,无双亲;如果 (i>1),则其双亲是结点 (floor(i/2)).
- 如果 (2i>n),则结点 (i) 无左孩子(结点 (i) 为叶子结点);否则其左孩子是结点 (2i).
- 如果 (2i+1>n),则结点 (i) 无右孩子,否则其右孩子是结点 (2i+1).
可以与上图结点理解。
二叉树的存储结构
二叉树的顺序存储结构
二叉树的顺序存储结构是用一维数组存储二叉树的结点,并且结点的存储位置,也就是数组的下标要能体现结点之间的逻辑关系。比如下面一棵完全二叉树:

将这棵二叉树存入到数组中,相应的下标对应其同样的位置,如下图:

对于一般的二叉树,尽管层序编号不能反映逻辑关系,但是可以将其按完全二叉树编号,只不过,把不存在的结点设置为空就行了。但是像极端的情况比如深度为 (k) 的右斜树,它只有 (k) 个结点,却需要分配 (2^k-1) 个存储单元空间,造成了极大的空间浪费,所以顺序存储结构一般只用于完全二叉树。
二叉链表
二叉树每个结点最多有两个孩子,所以为它设计一个数据域和两个指针域是比较自然的想法,我们称这样的链表叫做二叉链表。如图:

其中 data 是数据域, lchild 和 rchild 都是指针域,分别存放指向左孩子和右孩子的指针。二叉链表的结点结构定义代码如下:
typedef int TElemType; // TElemType 类型根据实际情况而定,这里假设为 int
struct BiTNode
{
TElemType data;
BiTNode *lchild, *rchild;
};
如果有需要,还可以再增加一个指向双亲的指针域,那样就称之为三叉链表。
遍历二叉树
二叉树的遍历(traversing binary tree)是指从根结点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问一次且仅被访问一次。
二叉树的遍历方式很多,如果我们限制了从左到右的习惯方式,那么主要分为四种:
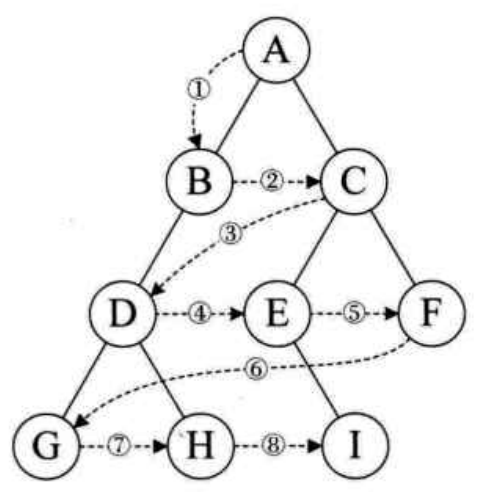
- 前序遍历。规则是若二叉树为空,则空操作返回,否则先访问根结点,然后前序遍历左子树,再前序遍历右子树。如图,遍历顺序为:ABDGHCEIF.
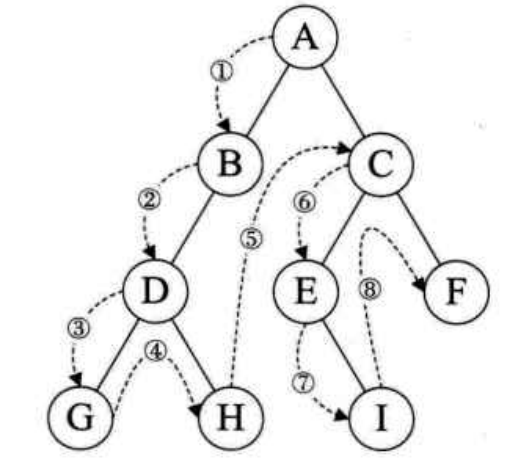
- 中序遍历。规则是若二叉树为空,则空操作返回,否则从根结点开始(注意并不是先访问根结点),中序遍历根结点的左子树,然后访问根结点,最后中序遍历右子树。如图,遍历顺序为:GDHBAEICF.
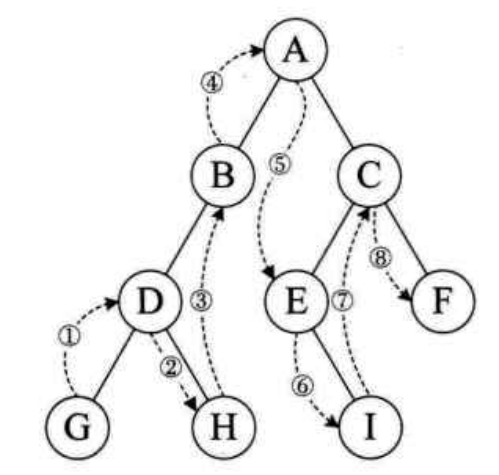
- 后序遍历。规则是若二叉树为空,则空操作返回,否则从左到右先叶子后结点的方式遍历访问左右子树,最后是访问根结点。如图,遍历顺序为:GHDBIEFCA.
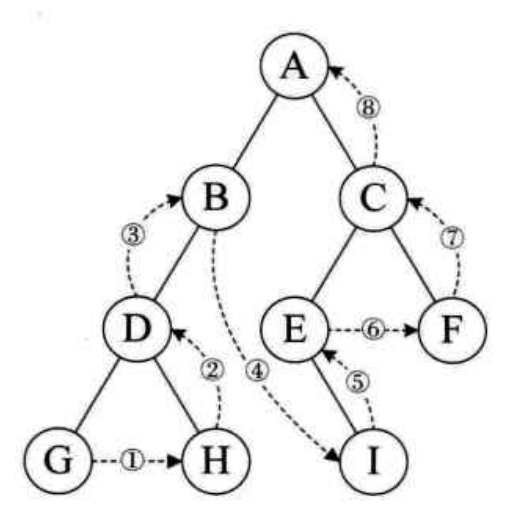
- 层序遍历。规则是若二叉树为空,则空操作返回,否则从树的第一层,也就是从根结点开始访问,从上而下逐层遍历,在同一层中,按从左到右的顺序对结点逐个访问。如图,遍历顺序为:ABCDEFGHI.
二叉树树的建立与遍历代码实现
如果我们要在内存中建立一个如下左图这样的二叉树,为了能让每个结点确认是否有左右孩子,我们对它进行扩展,就右图的样子,也就是将二叉树中每个结点的空指针引出一个虚结点,其值为一个特定值,比如“#”。我们称这种处理后的二叉树为原二叉树的扩展二叉树。扩展二叉树就可以做到一个遍历序列确定一棵二叉树。比如右图的遍历序列就为 AB#D##C##.

有了这样的准备就可以着手建立二叉树了。创建二叉树同遍历方法一样,也有不同的创建方法。现在我们用前序实现二叉树的建议。代码如下:
#include<iostream>
#include<cstdio> //getchar()
using namespace std;
typedef char TElemType; // TElwmType 类型根据实际情况而定,这里假设为 int
struct BiTNode
{
TElemType data;
BiTNode *lchild, *rchild;
};
void CreateBiTree(BiTNode* (&T)) //这里传入的是指针的引用,因为牵扯到修改指针的值
{
//读入字符串 ch, 前序构造树
//cout<<"请输入创建一棵二叉树的结点数据"<<endl;
TElemType ch = getchar();
//cin>>ch;
if (ch == '#') //其中getchar()为逐个读入标准库函数
T = NULL;
else
{
T = new BiTNode;//产生新的子树
T->data = ch;
CreateBiTree(T->lchild);//递归创建左子树
CreateBiTree(T->rchild);//递归创建右子树
}
}
void PreOrderTraverse(BiTNode* T)
{
//前序遍历
if(T) //结点不为空时执行
{
cout<< T->data;
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
}
else
cout<<"";
}
void InOrderTraverse(BiTNode* T)
{
//中序遍历
if(T) //结点不为空时执行
{
InOrderTraverse(T->lchild);
cout<< T->data;
InOrderTraverse(T->rchild);
}
else
cout<<"";
}
void PostOrderTraverse(BiTNode* T)
{
//后序遍历
if(T) //结点不为空时执行
{
PostOrderTraverse(T->lchild);
PostOrderTraverse(T->rchild);
cout<< T->data;
}
else
cout<<"";
}
int main()
{
//const char* ch = "AB#D##C##";
BiTNode *T;
cout<<"创建树结构,请输入字符,‘#’ 代表空:"<<endl;
CreateBiTree(T); //输入 AB#D##C##
cout<<"创建完毕"<<endl;
cout<<T->data<<endl;
cout<<"前序遍历结果:"<<endl;
PreOrderTraverse(T);//输出 ABDC
cout<<endl;
cout<<"中序遍历结果:"<<endl;
InOrderTraverse(T); //输出 BDAC
cout<<endl;
cout<<"后序遍历结果:"<<endl;
PostOrderTraverse(T);//输出 DBCA
cout<<endl;
return 0;
}
上边主要的疑惑是指针的引用,暂时先参考二叉树建立,指针问题. 遇到修改指针的得注意了。