概要
参考《大话数据结构》,把常用的基本数据结构梳理一下。
本节介绍栈与队列。
栈
栈:栈是限定仅在表尾进行插入和删除操作的线性表。
我们把允许插入和删除的一端称为栈顶(top),另一端称为栈底(bottom),不含任何数据元素的栈称为空栈。栈又称为后进先出(Last in First Out)的线性表,简称 LIFO 结构。
栈的插入操作,叫作进栈,也称压栈、入栈。类似子弹入弹夹。
栈的删除操作,叫做出栈,也有的叫作弹栈。如同弹夹中的子弹出夹。
栈的顺序存储结构
既然栈是线性表的特例,那么栈的顺序存储其实也就是线性表顺序存储的简化,我们简称为顺序栈。
下面我们直接利用完整的代码解释相关操作。
#include<iostream>
using namespace std;
typedef int SElemType; // SElwmType 类型根据实际情况而定,这里假设为 int
const int MAXSIZE = 5;
//栈的顺序存储结构
struct SqStack
{
SElemType data[MAXSIZE];
int top; //用于栈顶指针,当存在一个元素时,top = 1,通常把空栈的判定条件定为 top = -1
};
//初始化一个空栈
void InitStack(SqStack* S )
{
S->top = -1;
}
//进栈操作
void EnStack(SqStack* S, SElemType e)
{
if(S->top+1 == MAXSIZE) //栈满
cout<<"栈已经满了,禁止插入"<<endl;
else
{
S->top++; //栈顶指针增 1
S->data[S->top] = e; //将元素 e 赋值给栈顶
}
}
//出栈操作
//若栈不空,则删除 S 中栈顶元素,用 e 返回其值
void DeStack(SqStack* S, SElemType *e)
{
if(S->top == -1) //栈为空的判断
cout<<"栈为空"<<endl;
else
{
*e = S->data[S->top]; //将栈顶元素赋值给 e
S->top--; // 栈顶指针减 1
}
}
int main()
{
SqStack* myS = new SqStack; // 不加动态内存会运行错误
InitStack(myS); //初始化空栈
SElemType e = 3;
EnStack(myS, e); //入栈操作
cout<<myS->data[myS->top]<<endl; //输出 3
SElemType *f = new SElemType;
DeStack(myS, f);
cout<<*f<<endl; //输出 3
return 0;
}
进栈入栈操作没有涉及到任何循环语句,因此时间复杂度均是 (O(1)).
栈的链式存储结构
栈的链式存储结构简称链栈。
栈只是栈顶来做插入和删除操作,栈顶放在链表的头部还是尾部呢?由于单链表有头指针,而栈顶指针也是必须的,那干吗不让它合二为一呢,所以比较好的办法是把栈顶放在单链表的头部。另外,都已经有了栈顶在头部了,单链表中比较常用的头结点也就失去了意义,通常对于链栈来说,是不需要头结点的。
对于链栈来说,基本不存在栈满的情况,除非内存已经没有可以使用的空间。但对于空栈来说,链表原定义是头指针指向空,那么链栈的空其实就是 top=NILL 的时候。
下面我们直接利用完整的代码解释相关操作。
#include<iostream>
using namespace std;
typedef int SElemType; // SElwmType 类型根据实际情况而定,这里假设为 int
//const int MAXSIZE = 5;
//栈的链式存储结构
struct StackNode
{
SElemType data;
StackNode* next; //从栈顶的方向指向栈底
};
struct LinkStack
{
StackNode* top; //用于栈顶指针
int counts; // 记录栈中元素个数
};
//初始化一个空栈
void InitStack(LinkStack* S )
{
S->counts = 0;
}
//进栈操作
void EnStack(LinkStack* S, SElemType e)
{
StackNode* s = new StackNode;
s->data = e;
s->next = S->top; //把当前的栈顶元素赋值给新结点的直接后继
S->counts++; //栈顶指针增 1
S->top = s; //将新的结点 s 赋值给栈顶指针
}
//出栈操作
//若栈不空,则删除 S 中栈顶元素,用 e 返回其值
void DeStack(LinkStack* S, SElemType *e)
{
if(S->counts == 0) //栈为空的判断
cout<<"栈为空"<<endl;
else
{
*e = S->top->data; //将栈顶元素赋值给 e
S->top = S->top->next; // 栈顶指针减 1
S->counts--; //元素数减一
}
}
int main()
{
LinkStack* myS = new LinkStack; // 不加动态内存会运行错误
InitStack(myS); //初始化空栈
SElemType e = 3;
EnStack(myS, e); //入栈操作
cout<<myS->top->data<<endl; //输出 3
SElemType *f = new SElemType;
DeStack(myS, f);
cout<<*f<<endl; //输出 3
return 0;
}
进栈入栈操作没有涉及到任何循环语句,因此时间复杂度均是 (O(1)). 如果栈的使用过程中元素变化不可预料,有时很小,有时非常大,那么最好是用链栈,反之,如果它的变化在可控范围内,建议使用顺序栈更好一些。
栈的应用---递归
栈有一个很重要的应用:有程序设计语言中实现了递归。
用递归实现斐波那契数列。代码如下
int Fbi(int i)
{
if(i == 0 || i == 1)
return i;
if (i > 1)
{
return Fbi(i-1)+Fbi(i-2); //调用自己
}
}
int main()
{
cout<< Fbi(5);
return 0;
}
为了理解,我们可以不要把一个递归函数中调用自己的函数看作是在调用自己,而就当它是在调用“另一个”函数,只不过,这个函数和自己长得一样而已。我们来模拟代码中 Fbi(i) 函数当 i=5 的执行过程,如下图
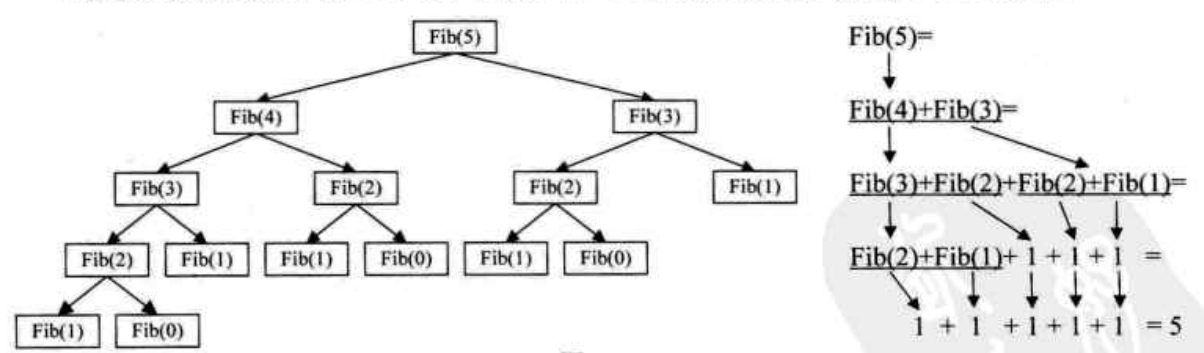
前面我们看到递归是如何执行它的前行和退回阶段的。递归过程退回的顺序是它前行顺序的逆序。在退回过程中,可能要执行某些动作,包括恢复前行过程中存储起来的某些数据,这种存储某些数据,并在后面又以存储的逆序恢复这些数据,以提供之后使用的需求,显然 很符合栈这样的数据结构,因此,编译器使用栈实现递归就没什么好惊讶的了。简单地说,就是在前行阶段,寻每一层递归,函数的局部变量、参数值以及返回地址都被压入栈中。在退回阶段,位于栈顶的局部变量、参数值和返回地址被弹出,用于返回调用层次中执行代码的其余部分,也就是恢复了调用的状态。
队列
队列:是只允许在一端进行插入操作,而在另一端进行删除操作的线性表。
我们把允许插入的一端称为队尾,允许删除的一端称为队头。队列是一种先进先出(First in First Out)的线性表,简称 FIFO 结构。
队列的顺序存储结构及实现
我们假设一个队列按数组的形式存储,当队列进行插入和删除操作时,队列中的所有元素都得向前移动,以保证队列的队头。也就是下标为 0 的位置不为空,此时时间复杂度为 (O(n)),这像现实中大家排队买票,前面的人买好了离开,后面的人就是全部向前一步,补上空位,似乎没什么不好。可想想,如果不去限制队列的元素必须存储在数组的前 (n) 个单元这一条件,出队的性能就会大大增加。也就是说,队头不需要一定在下标为 0 的位置。
为了避免当只有一个元素时,队头和队尾重合使处理变得麻烦,所以引入两个指针, front 指针指向队头元素,rear 指针指向队尾元素的下一个位置,这样当 front 等于 rear 时,此队列不是还剩一个元素,而是空队列。
队列的整体移动会面临一个问题,就是有可能跑到数组之外。假设一个队列的总个数不超过 5 个,但目前总共 3 个元素已经移动到数组末尾,再进行插入操作的话,就会产生数组越界的错误,可实际上,队列在下标为 0 和 1 的地方还是空闲的。这种现象叫做“假溢出”。 为了解决这个问题,就再从头开始,也就是头尾相接的循环。我们把队列的头尾相接的顺序存储结构称为循环队列。
下面我们直接利用完整的代码解释相关操作。
#include<iostream>
using namespace std;
typedef int QElemType; // QElwmType 类型根据实际情况而定,这里假设为 int
const int MAXSIZE = 5;
//循环队列的顺序存储结构
struct SqQueue
{
QElemType data[MAXSIZE];
int fro; //头指针
int rear; //尾指针,若队列不空,指向队尾元素的下一个位置
};
//初始化一个空队列
void InitQueue(SqQueue* Q )
{
Q->fro = 0;
Q->rear = 0;
}
//循环队列求队列长度代码如下
int QueueLength(SqQueue Q)
{
return(Q.rear - Q.fro + MAXSIZE) % MAXSIZE;
}
//循环队列的入队操作
void EnQueue(SqQueue* Q, QElemType e)
{
//为了避免当 rear = fon 时,不知道队列是空还是满,故总留一个空位置,所以下面判断有 +1
if((Q->rear+1)%MAXSIZE == Q->fro) //队列满的判断
cout<<"队列已经满了,禁止插入"<<endl;
else
{
Q->data[Q->rear] = e; //将元素 e 赋值给队尾
Q->rear = (Q->rear+1) % MAXSIZE; // rear 指针后移一个位置,若到最后则转到数组头部
}
}
//循环队列的出队操作
//若队列不空,则删除 Q 中队头元素,用 e 返回其值
void DeQueue(SqQueue* Q, QElemType *e)
{
if(Q->fro == Q->rear) //队列空的判断
cout<<"队列为空"<<endl;
else
{
*e = Q->data[Q->fro]; //将队头元素赋值给 e
Q->fro = (Q->fro+1) % MAXSIZE; // fro 指针向后移动一位,若到最后则转到数组头部
}
}
int main()
{
SqQueue* myQ = new SqQueue; // 不加动态内存会运行错误
InitQueue(myQ); //初始化队列
QElemType e = 3;
EnQueue(myQ, e); //入队操作
cout<<myQ->data[myQ->fro]<<endl; //输出 3
QElemType *f = new QElemType;
DeQueue(myQ, f);
cout<<*f<<endl; //输出 3
return 0;
}
下面研究不需要担心队列长度的链式存储结构。
队列的链式存储结构及实现
队列的链式存储结构,其实就是线性表的单链表,只不过它只能尾进头出而已,我们把它简称为链队列。为了操作上的方便,我们将队头指针指向链队列的头结点,而队尾指针指向终端结点。
下面我们直接利用完整的代码解释相关操作。
#include<iostream>
using namespace std;
typedef int QElemType; // SElwmType 类型根据实际情况而定,这里假设为 int
//const int MAXSIZE = 5;
//队的链式存储结构
struct QueueNode
{
QElemType data;
QueueNode* next; //指向队尾的方向
};
struct LinkQueue
{
QueueNode* fro; //指向队头
QueueNode* rear; //指向队尾
//int counts; // 记录队中元素个数
};
void InitQueue(LinkQueue *Q) //构造一个空的队列
{
QueueNode *q = new QueueNode; //申请一个结点的空间
q->next = nullptr; //当作头结点
//队首与队尾指针都指向这个结点,指针域为NULL
Q->rear = q;
Q->fro = Q->rear;
}
//进队操作
void EnQueue(LinkQueue* Q, QElemType e)
{
QueueNode* q = new QueueNode;
q->data = e;
q->next = nullptr; //最后一个元素指向空指针
Q->rear->next = q; //把原先队尾指针指向新添加的节点
Q->rear = q; //把当前的 s 设置为队尾
}
//出队操作
//若队不空,则删除 Q 中栈顶元素,用 e 返回其值
void DeQueue(LinkQueue* Q, QElemType *e)
{
if(Q->fro == Q->rear)
cout<<"空队"<<endl;
else
{
*e = Q->fro->next->data; //将队头元素赋值给 e. Q->fro 是头结点,但是不存数据,所以得有 next
Q->fro = Q->fro->next; //队头指针减 1
}
}
int main()
{
LinkQueue* myQ = new LinkQueue; // 不加动态内存会运行错误
InitQueue(myQ);
QElemType e = 3;
EnQueue(myQ, e); //入栈操作
cout<<myQ->rear->data<<endl; //输出 3
QElemType *f = new QElemType;
DeQueue(myQ, f);
cout<<*f<<endl; //输出 3
if(myQ->rear == myQ->fro)
cout<<"目前是空队列"<<endl;
return 0;
}
总结
栈和队列都是特殊的线性表,只不过对插入和删除操作做了限制。
- 栈是限定仅在表尾进行插入和删除操作的线性表
- 队列是只允许在一端进行插入操作,而在另一端进行删除操作的线性表
它们都可以用线性表的顺序存储结构来实现,但都存在着顺序存储的一些弊端。对于栈来说,如果是两个相同数据类型的栈,则可以用数组的两端作栈底的方法来让两个栈共享数据,这就可以最大化地利用数组的空间。对于队列来说,为了避免数组插入和删除时需要移动数据,于是就引入了循环队列,使得队头和队尾可以在数组中循环变化。
它们也都可以通过链式存储结构来实现,实现原则上与线性表基本相同。