计算机系统结构 学习笔记(浮点数据表示)

浮点数的数据表示

浮点数的数据表示浮点数N可以用如下方式表示

N=m×r_m^e

在浮点数据表示方式中有6个参数:

尾数的值m;阶码的值e;尾数的基r_m;阶码的基r_e;尾数长度p;阶码长度q。

浮点数在数据存储单元中的存放方式如图所示。

原码:机器数的最高一位代表符号,0代表正号,1代表负号,以下各位给出数值绝对值的表示法。零有正零和负零两种表示形式。

补码:机器数的最高一位代表符号,0代表正号,1代表负号。若为正数,数的补码和原码相同。若为负数,以下各位为原码按位求反后,最后一位加1来表示。零只有一种表示形式,即原码中的正零。负零的表示,当为纯小数,则为-1。当为纯整数,则为2^n,n为数值位的位数。

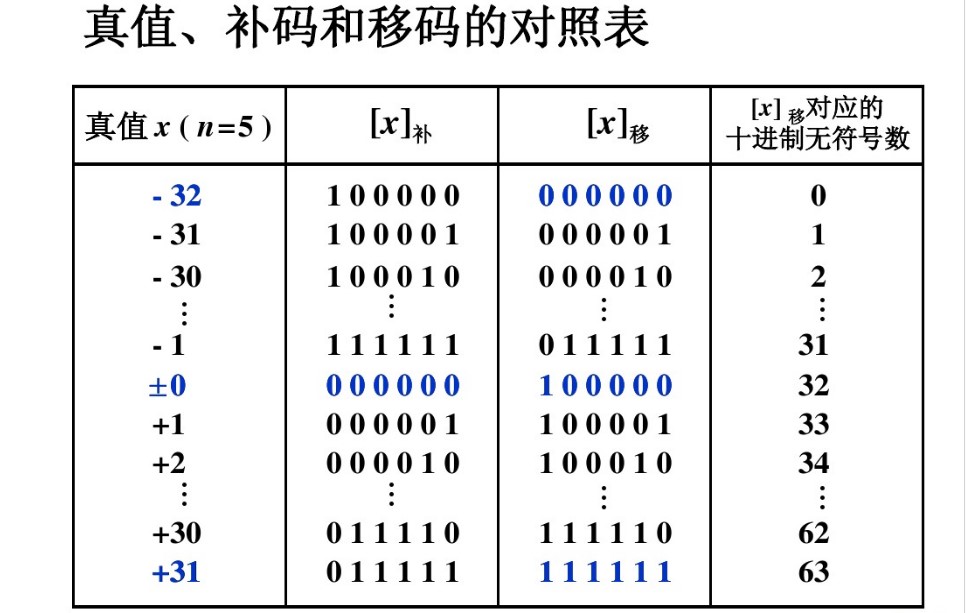
移码:以1位符号位和n位数值位的整数为例,移码由数值自身于2^n相加得到。

规格化浮点数:以尾数采用补码方式为例,尾数的最高位和符号位相反。符号位为0,尾数最高位为1。符号位为1,尾数最高位为0。

浮点数的表数范围

在大多数《计算机组成原理》课程中讲解浮点数表示时,侧重浮点数在运算器中运行的过程,给出的规格化以双符号位为原则。在《计算机系统结构》课程中,浮点数的表示尾数符号为单符号位表示形式。根据码制和正负数分类,总结出规格化的定义,推算尾数的取值范围,这样就不必死记硬背给出的表数范围表。

 

下面以尾数基值r_m取2和16,尾数用原码或补码、纯小数表示,阶码用移码、整数表示的规格化浮点数为例,研究表数范围。

1.尾数采用原码的取值范围

规格化定义1:当浮点数尾数采用原码、纯小数形式表示时,规格化的浮点数尾数最高位为非零。

例1:浮点数尾数基值r_m=2,p=8,q=6,整个浮点数长度为:p+q+2=16位二进制。正尾数取值范围为0.10000000B……0.11111111B,对应十进制数为2^-1……1-2^-8;负尾数取值范围为1.10000000B……1.11111111B,对应十进制数为-(2^-1)……-(1-2^-8)正负尾数取值完全对称。

例2:浮点数尾数基值r_m=16=2^4,p=2,q=6,整个浮点数长度为:p^4+q+2=16位二进制。正尾数取值范围为0.10H……0.FFH,对应的十进制数为16^-1……1-16^-2;负尾数取值范围为1.10H……1FFH,对应的十进制数为-(16^-1)……-(1-16^-2)。

结论1:尾数用原码、纯小数时规格化尾数的取值范围为:最大正尾数1-r_m^-p,最小正尾数r_m^-1,最大负尾数-(r_m^-1),最小负尾数-(1-r_m^-p)。

 

2.尾数采用补码的取值范围

规格化定义2:当浮点数尾数采用补码、纯小数形式表示时,规格化正尾数的浮点数尾数最高位为非零。

根据补码定义可知,正数的补码和原码相同,所以上面的例子在尾数中采用补码、纯小数形式表示的规格化正尾数取值范围和原码表示形式相同。

规格化定义3:当浮点数尾数采用补码、纯小数形式表示时,规格化负尾数的浮点数尾数最高位不能为1-r_m^-1。

在浮点数尾数基值r_m=2的例1中,规格化补码表示范围为1.00000000B……1.01111111B,根据补码定义可以得到所有可以表示的尾数值,最大负尾数的补码形式为1.01111111B,对应十进制为2^-1+2^-8。最小负尾数的补码形式为1.00000000B,对应的十进制为-1。在浮点数尾数基值r_m=16的例子中,根据定义3,尾数最高位不能取16^-1,规格化补码负尾数的取值范围为1.00H……1.EFH,最大负尾数的补码形式为1.EFH,对应的十进制数为16^-1+16^-2,最小负尾数的补码形式为1.00H,对应的十进制数为-1。

结论2:尾数用补码、纯小数时规格化尾数的取值范围为:最大正尾数1-r_m^-p,最小正尾数r_m^-1,最大负尾数-(r_m^-1+r_m^-p),最小负尾数-1。

  

3.浮点数阶码的取值范围

浮点数表示中阶码通常采用基值为2,以移码形式表示的纯整数。由于移码的码制在相关课程中仅仅给出定义和使用场所,没有相关的运算联系,在用移码表示浮点数阶码时,非常容易混淆,下面将介绍一种浅显易懂的表示方法。

将浮点数的q位阶码长度和1位符号位拼接在一起,构成q+1位的二进制数,采用此q+1位二进制数表示一个无符号的机器数,即浮点数阶码的移码表示形式,表示范围为0……2^(q+1)-1。给出一个q+1位的移码值,则对应的十进制数为:移码-2^q。相反,给出一个合法的阶码值,通过“阶码值”+2^q得到阶码在浮点数存储单元中移码的存放方式。

在例1中,阶码长度为8,加上1位阶符,则阶码的移码表示形式000000000……111111111,对应阶码的十进制数取值范围为0-2^8……2^9-1-2^8,任意给出阶码取值范围中的一个数,在阶码在数据存储单元中的移码存放方式,即可得到。同样,在例2中,加上一位阶符的阶码的表示形式0000000……1111111,对应的十进制数为0-2^6……2^7-1-2^6。

结论3:阶码采用移码表示的取值范围为:最大阶码r_e^q-1,最小阶码-r_e^q。

阶码采用移码表示好处通过上表也可以得到很好的验证——保证浮点零与机器零的一致性，有利于软硬件设计！（在除移码之外的所有码制中，最小负数都不是全0（包括符号位））

 

例题：已知一个字长为32位的机器，尾数用纯小数、原码表示，rm=2，p=24；阶码用整数、移码表示，re=2，q=6；其格式最左边为尾数符号位，最右边位尾数，中间放阶符和阶码。请问浮点数C2D00000表示十进制数值是多少？这样的机器浮点数表示范围是多大？并用二进制写出它的浮点数0。

[解答]：

C2D00000（1100 0010 1101 0000 0000 0000 0000 0000）

移码表示的阶码1000010（最高位为阶符）-->转成对应的十进制数0000010（+2）

尾数显然易得-->  -0.8125

故所得十进制数值为-0.8125*2^(2^2)=13

 

结合前面讨论的结论1和结论3

这样的机器规格化浮点数N表数范围为：

r_m^(-1)*r_m^ (-r_e^q) =<|N|<= (1-r_m^(-p))* r_m^(r_e^q-1)

即2^(-1)*2^(-2^6)=<|N|<=(1-2^(-24))*2^(2^6-1)

 

二进制浮点0表示：

         00000000 0000 0000 0000 0000 0000 0000

【附:一文一图】