復數運算
虛數有一個直觀化的解釋：它把數字“旋轉”，就像負數把數字做了“鏡像”一樣。這種深刻的見解使得我們理解復數的元算變得十分簡單並且清晰，而且也可以很好的檢查一下你是否學會了這種見解。以下是我們的作弊表：
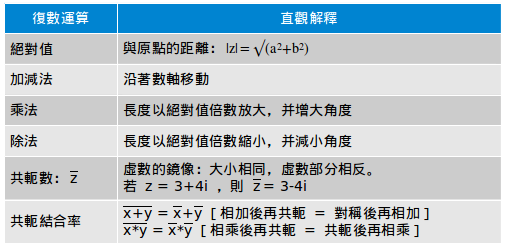
這一章我們將逐一檢驗一遍我們的直觀化的解釋。
6.1 復變量
在常規代數中，我們經常說“x=3”，這樣很好——有一個變量x，它的值是3。而在復數中，我們就會發現：有兩個維度需要討論。寫下：
z=3+4i
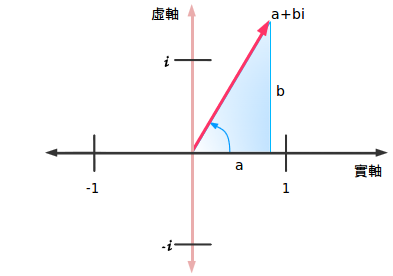
我們就是在說有一個變量z，它有兩部分：3（實數部分）與4i（虛數部分）。一個數有兩部分看上去有些怪，但是我們已經用過這種表示方法了。我們經常會寫：
y
y有一個整數部分（3）與一個分數部分（0.4或4/10）並不會影響我們理解它。Y是兩部分的組合。復數也與之類似：在一個變量中它包含有實數部分與虛數部分（通常縮寫為Re與Im）。
不幸的是，我們沒有辦法把它們“合起來”記作一個數（像3.4那樣）。我有一個辦法把用黑筆把虛數部分垂直的寫在虛數上方，但是這種方法並不流行。所以我們還是繼續使用“a+bi”的形式吧。
6.2 測量大小
因為復數有兩個獨立的數軸，我們發現它的大小可以使用勾股定理：
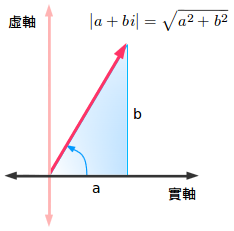
那麼，復數3+4i的大小就是5。通常記作：|z|。
看起來很像是絕對值吧？其實從某種角度來看，它就是絕對值。|z|描述了復數距離零點的距離，就像是絕對值表示負數距離零點的距離一樣。
6.3 復數的加法與減法
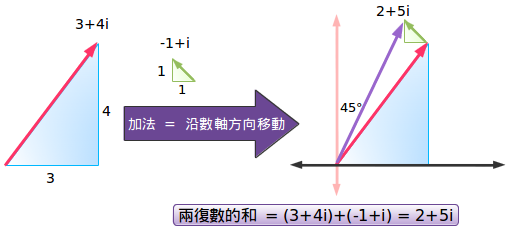
我們通常見到的加法可以被認為是“移動”一段數字而得到。復數的加法也可以這樣類比，不過我們有兩個維度（實數與虛數）可以移動。舉個例子：
、
(3+4i)與(-1+i)相加就可以得到2+5i。
再一次的，這種可視化的解釋幫助我們理解“獨立的部分”是如何組合在一起的：實部與虛部各自處理再組合就可以了。
減法就是加法的逆——就是把它向相反的方向移動。減去(1+i)就是加上-1·(1+i)，或者是加上(-1-i)。
6.4 復數的乘法
這裏數學就會變得很有趣。我們把兩個復數（x，y）相乘得到z：
角度相加：角度（z）＝角度（x）+角度（y）
長度相乘：|z|=|x||y|
這就是說，z的角度是x的角度與y的角度的和，而長度就是它們的乘積。無論你相信與否，復數的這種性質幫了數學很大的忙！
長度相乘有它的意義——我們在一般的乘法中就是這麼做的（3×4就是把3跟4的長度相乘）。角度的相加需要更詳細的討論，我們以後再談（很好奇嗎？看看正余弦函數是如何相加的，並把它們與(a+bi)·(c+di)比較一下）。
現在舉另一個例子：我們把z＝3+4i乘以它自己。在做數學運算前，我們已經知道：
長度的結果會是25.因為z的長度為5，所以|z|·|z|＝25
角度的結果是大於90度。因為3+4i的角度大於45度（因為3+3i正好是45度），所以翻倍後比90度大。
接下來我們做數學運算：
(3+4i)·(3+4i)＝9+16i2 +24i＝-7+24i
現在來檢查一下我們預測：
長度：(−7)2+242−−−−−−−−−−√=625−−−√=25
跟我們的預測相符
角度：因為-7是負的而24i是個正的， 我們便知道我們要“向後並向上”，這就是說將跨過90度（“直直的”）。專業一點就是，我們計算arctan(24/-7)=106.2度（記住我們在第二象限）。這個也驗證了我們的猜想。
漂亮。我們做數學運算時，還可以用我們關於旋轉與大小的直觀化認識來幫助我們檢查結果。如果最後的結果小於90度（比如說，向前又向上），或者我們的長度不是25，我們便知道計算出了一些問題。
6.5 復數的除法
除法就是乘法的逆運算。就像減法是加法的逆運算一樣。復數相除時（x/y），我們可以知道：
角度相減：角度（z）＝角度（x）－角度（y）
長度相除：|z|=|x|/|y|
看起來很不錯。現在讓我們做一做這個除法：
(3+4i)/(1+i)
呃，該從哪裏開始呢？我們應該怎麼做這個除法呢？通常的代數解法並不能幫不上什麼忙，更不用說還有一個古怪的i（先生，先生，你知道1/i＝－i嗎？兩邊同乘以i再看看一看啊。）幸好我們還有捷徑可走。
6.6 引入復數的共軛
我們做復數除法的第一個目標就是把角度相減。我們怎麼做呢？乘以與它相反的角度！這就會“加上”一個負的角度，等價於做了一次角度減法。
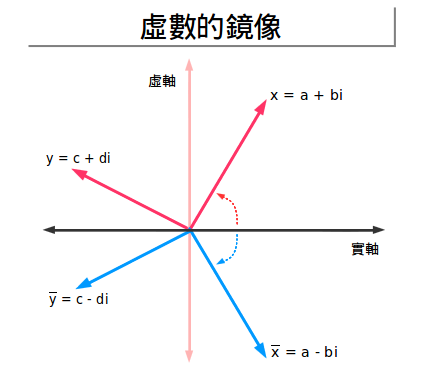
不再是z+bi，現在考慮以下z* ＝a-bi，叫作“復數共軛”。實部相等，但是虛部是一個“鏡像”。復數共軛或者說“想像的一種反射”有著相同的長度，但是角度相反！
所以，乘以a-bi就是減去一個角度。很簡潔。
復數共軛用星號（z* ）或者是橫線表示(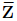
)——數學家喜歡爭論這些表示法的好壞。不管哪種表示方法，復數的共軛都是把它們的虛部翻轉而已：
z＝a+bi
它的復數共軛就是：
z* ＝a-bi
註意，b不一定是要“負的”。如果z＝3-4i，那麼z* ＝3+4i。
6.7 乘以復數的共軛
如果乘以一個復數乘以它的共軛會發生什麼呢？z乘以z* 等於多少呢？看看這個：
z·z* ＝1·z·z*
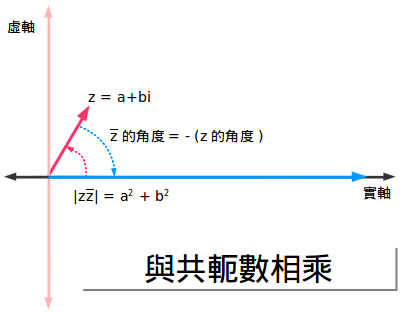
所以我們選擇一個1（一個實數），加上z的角度，再加上z* 的角度。但是最後一個角度是負的——是個減法！所以我們最終的結果就是一個實數，因為我們把角度消掉了。數字就是|z|2 ，因為我們把大小乘了兩次。
現在讓我們再做一個例題：(3+4i)(3-4i)=9-16i2 =25
我們得到了一個實數，正如我們所預料的！數學愛好者同樣可以試一試這個代數運算：
(a+bi)(a-bi)=a2 +abi-abi+b2i2= a2 + b2
啊哈！最後結果沒有虛數部分，而隻是大小的平方。我們把復數的共軛認為是一種“反方向旋轉”幫助我們預測到了這一結果。
6.8 改變的你的數字
我們乘以一個共軛z* ，就相當於乘以一個|z*|。為了得到相反的效果，我們可以除以|z|，而要再是縮小了|z|我們再除一次即可。總的來說，如果我們乘以一個復共軛那麼我們就需要除以|z||z|來保持原數不變。
6.9 向我展示除法！
我之前迴避了一些除法，現在是見證奇跡的時刻。如果我們想計算
(3+4i)/(1+i)
我們可以馬上得到：
旋轉一個相反的角度：乘以(1-i)而不是(1+i)
除以長度的平方：除以|21/2|2 =2
答案是：
(3+4i)/(1+i)＝(3+4i)(1-i)(1/2)=(3-4i2 +4i-3i)(1/2)=7/2+(1/2)i
更常見的方法是上下同乘以分母的復共軛。
我們通常隻是被告訴“隻管上下同乘以它的復共軛”就行了，而從來沒能明白其中的原因。今天我們搞明白了。
兩種方法都可以（通常使用後一種方法），但是用其中一種檢查另外一種也是個不錯的主意。
6.10 更多的數學技巧
現在我們既然理解了復共軛，這裏有幾個關於復共軛的性質：
(x+y)* = x* + y*
(x·y)* = x* · y*
第一個很容易理解，兩個數的和再“反射（求共軛）”等價於把它們的共軛相加。另一種理解的辦法是：移動兩個數然後再取反等價於同時把兩個數移動並取反。
第二個性質就比較難理解了。沒錯，代數運算或許可以，但是更直觀的解釋是什麼呢？（x·y）* 的結果就是：
把長度相乘：|x|·|y|
把角度相加並取共軛（相反）：角度（x）+角度（y）變為 -角度（x）+ －角度（y）
而x* 乘以y* 就是：
長度相乘：|x|·|y|（更上面的相同）
共軛角度相加：角度（x*）+角度（y*）＝-角度（x*）+-角度（y*）
啊哈！我們得到了相同的結果，而我們不需要用傳統的代數方法。代數方法也可以，但是並不是最讓人滿意的解釋。
6.11 一個簡單示例
共軛就是“撤銷”一次旋轉。試著這樣考慮：
我存了3,
10,15.75,
23.5到我的帳戶。什麼交易會把這些交易抵消呢？相反的操作：加上它們，然後乘以-1.
我通過幾次相乘把一套直線做了幾次旋轉：(3+4i),(1+i),(2+10i)。什麼樣的操作會把這些旋轉抵消呢？相反的操作：乘以這些復數，取它們的復共軛便得到結果。
看到了吧，復共軛就是相當於一種撤銷操作，就像負數撤銷了相加的效果一樣。警告：處理復共軛時，你需要除以|z||z|這樣才能抵消它們對大小的影響。
6.12 最後的一些想法
這裏的數學並沒有什麼新的東西，但是我一直沒意識到復共軛是怎麼發揮作用的。為什麼是a-bi而不是-a+bi呢？復共軛並不是一個隨意的選擇，是從虛數角度考慮的一種鏡像，正好就是相反的角度。
看到把虛數看作旋轉給了我們一種解決問題的新思路；“乘上再消去”給了我們一種直覺，即使是討論像復數一樣怪異的話題。希望你能享受到快樂的數學。
本網站無註明「轉載」的著作均由Jak Wings製作 CC BY-NC-SA 2.5
Creative Commons 保持署名-相同方式分享 2.5
原文地址：http://jakwings.is-programmer.com/posts/29550.html