字符串匹配的暴力解法
给定字符串s和p,寻找字符串p在字符串s中出现的位置,暴力解法如下所示:
- 如果当前字符匹配成功,
++i;++j,继续匹配下一字符。 - 如果
s[i]与s[j]匹配失败,令i-=(j-1),j=0,即i转到上次首次匹配开头字符的下一位置,j从头开始。
int brute_match(string s, string p) {
int slen = s.size();
int plen = p.size();
int i = 0, j = 0;
while (i < slen and j < plen) {
if (s[i] == p[j]) {
++i;
++j;
} else {
i -= (j - 1);
j = 0;
}
}
if (j == plen)
return i - j;
return -1;
}
如果有一种算法能够不让i回退,只需要移动j,那么我们的算法将会大为简化。
kmp算法
在kmp算法中,引入了next数组,表示当前字符之前的子字符串中具有多大长度的相同的前缀后缀,请注意,next字符串的内容是和需要匹配的字符串p相关的。
在brute-force算法的基础上改进的kmp算法如下所示:
int kmp_match(string s, string p,const vector<int> &next) {
int slen = s.size();
int plen = p.size();
int i = 0, j = 0;
while (i < slen and j < plen) {
if (j == -1 or s[i] == p[j]) {
++i;
++j;
} else {
j = next[j];
}
}
if (j == plen)
return i - j;
return -1;
}
next数组的求法
首先,我们思考一下如何计算给定字符串的最长相同前缀和后缀的长度。
- 设最长相同前缀后缀为
str - 设数组
len中每一个位置和字符串s一对应,表示字符串截止到当前位置最长相同前缀后缀的长度。 k表示当前位置及之前的字符串的最长相同前缀后缀的长度。s[k]表示原字符串s在最长前缀后缀str之后紧跟的那个字符。- 我们从第2个字符开始寻找最长前缀后缀,如果
s[i]!=s[k],代表字符i无法进一步与字符j匹配,最长相同前缀后缀不可能在上一次匹配的基础之上进一步增长。如果之前能够匹配的最长相同前缀后缀长度大于0,我们不断尝试在上一次的基础之上降低标准,匹配更小长度的最长前缀后缀。 - 关键点在于,如何选择降低标准后的需要匹配的相同前缀后缀?这里我们将
k调整为k=len[k-1],原因稍后详述。 - 若最终经过调整之后,
s[i]=s[j],这表示最长相同前缀与后缀能够在长度为k的最长相同前缀后缀的基础之上,再增长一个字符,即len[i]=++k。否则说明当前位置没有相同前缀后缀,记len[i]=0。
只有长度大于1的字符串才有最长前缀与后缀,最长前缀不包括最后一个字符,最长后缀不包括第一个字符。
k=len[k-1]原因讲解
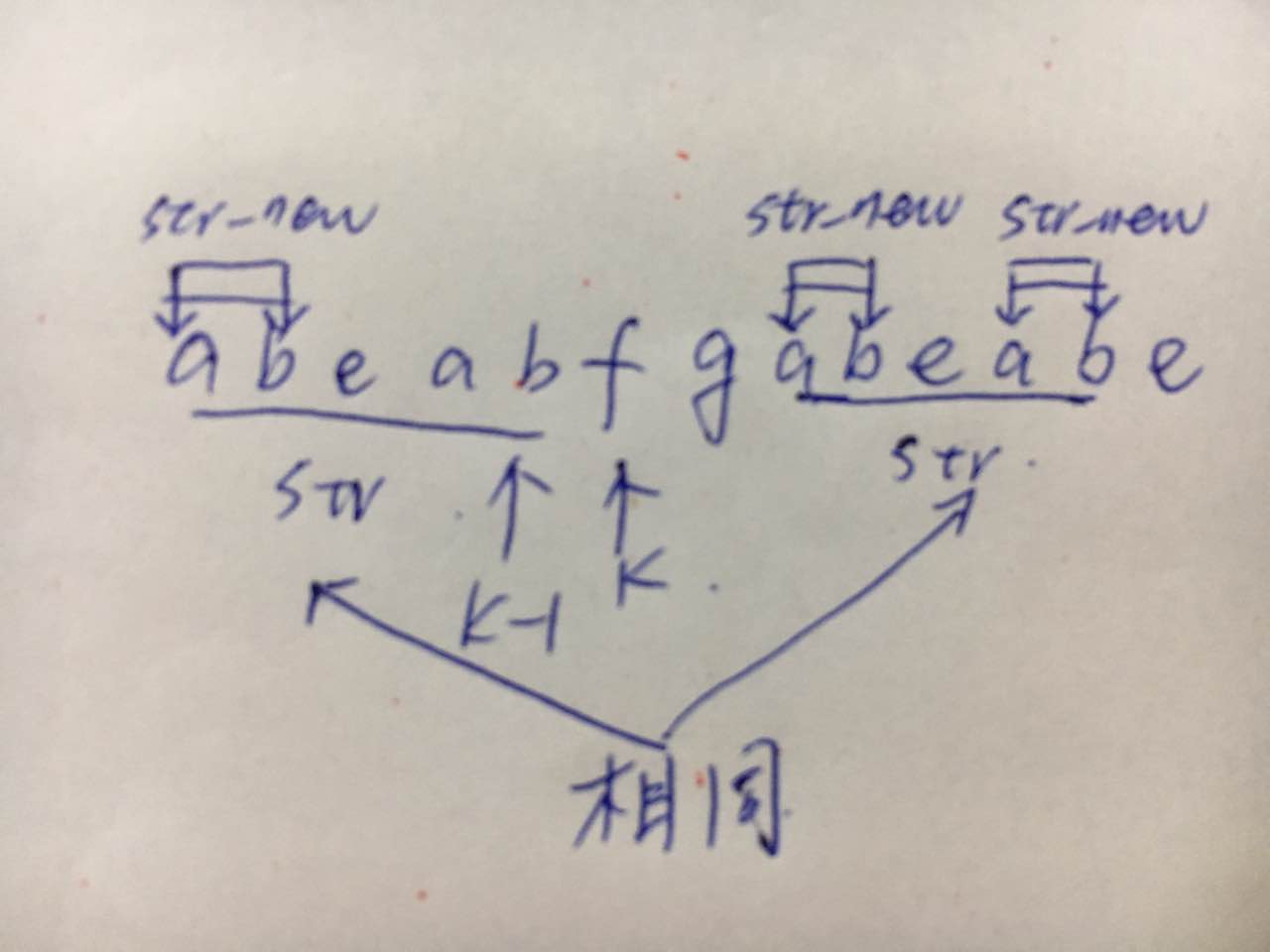
假设当前k指向字符串中f对应的位置,在e之前我们匹配到的最长相同前缀后缀为abeab,我们发现e与f不能匹配,我们需要降低标准,尝试匹配更短长度的最长前缀后缀,应该匹配多长的呢?
我们发现图中下划线部分的字符串str完全相同,我们要找的长度缩减的最长相同前缀后缀长度不能超过str的长度,而且要保证这一字符串(设为str_new)满足条件:是相同的前缀后缀。即图中最前面和最后面标记的字符串str_new必须完全一样。根据对称性,这等价于在靠后的str中寻找最长前缀后缀。而且因为k比较的时候,k实际指向前面str的末尾下一位置,所以我们有:k=len[k-1]。
void calculate_length(string s, vector<int> &len) {
len.resize(s.length());
len[0] = 0;
int k = 0;
for (int i = 1; i < s.length(); ++i) {
while (s[i] != s[k] and k > 0) {
k = len[k - 1];
}
if (s[i] == s[k]) {
len[i] = ++k;
} else {
len[i] = 0;
}
}
}
next数组与最长前缀后缀
next数组,表示当前字符之前的子字符串中具有多大长度的相同的前缀后缀,也就是说next 数组相当于“最大长度值” 整体向右移动一位,然后初始值赋为-1。
其示例代码如下所示,因为和求最长前缀后缀的代码类似,故不再追究。
void calculate_next(string s,vector<int>&next){
next.resize(s.length());
int len = s.length();
next[0] = -1;
int k = -1;
int j = 0;
while(j<len-1){
if(k == -1 or s[j] ==s[k]){
++k;
++j;
next[j] = k;
}
else{
k = next[k];
}
}
}