第一单元的三次作业都是关于多项式表达式求导的问题,难度层层递进,主要是一个基本的熟悉过程,熟悉Java,熟悉面向对象。单线程操作,总体思维较为清晰。
第一次作业
类图
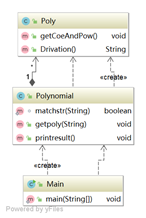

第一次作业输入形式较为标准,为标准的多项式,结构比较简单清晰,求导部分算法简洁,主要的难点在于输入的识别和合并同类项。
在识别输入的多项式这方面,使用了正则表达式匹配的方法,通过构建正确表达式的正则式来规避输入的错误格式。但是这样大串的正则匹配容易出现栈溢出问题,解决的方法主要有两种:小正则单项匹配和独占模式。我在自己的代码中使用了replaceall方法将匹配到的单项替换为空,该方法实现较为简洁。在拆分一个个项的过程里,我使用了Pattern类里的group方法。
由于本次作业我未考虑合并同类项,导致性能分低,在第二次作业中做了合并的补充。
互测环节中主要的错误是漏考虑\s匹配到的其他空白字符。
Hack的方式主要是通过查看对方正则表达式的书写进行针对性的测试,还有一些栈溢出、空格符的较常见的错误。
第二次作业
类图
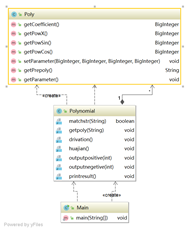
本次作业在第一次作业的基础之上加入了正余弦函数和单项的多个因子相乘,但是并未出现嵌套函数,所以可以总体将每一个项整合为统一的格式,形如coe*x^a*sin(x)^b*cos(x)^c。经过整合之后求导规则固定单一,所以求导仍旧不是难点,问题仍然主要在表达式输入识别和合并同类项上。
在输入处理方面,判断非法格式的方法与第一次作业基本相同,经过一系列去空格去符号的预处理后将表达式拆分成单项,每个项再拆分成因子,同时完成因子的合并形成标准格式,提取相应的参数。
在合并方面,直接判断三类因子的指数是否完全相同便可合并。其余还有一些小的优化如1*、0*、^1等。
在互测环节中由于前期测试的不足,未能发现合并时系数相乘的错误,损失惨重。
Hack的方式基本等同第一次作业
第三次作业
类图
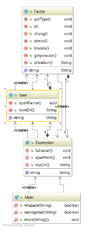

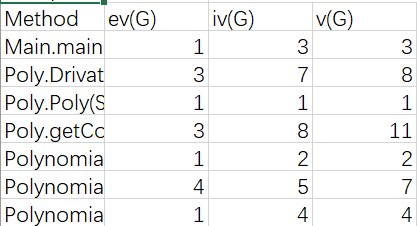
第三次作业相较于前两次的作业难度有了较大的提升,输入的表达式含有嵌套因子,多项式因子,形式不定,求导需要递归,所以难点有三:输入识别,函数求导和表达式化简。
在输入识别方面,由于嵌套因子和表达式因子,无法再使用大正则匹配所有,检查格式错误的方法从“找正确“变成了“排错误“,因此情况较为繁琐,容易缺漏,因此需要一定的预处理。先排除所有的空格错误字符错误,然后去除空格;再排除符号错误,删去冗余符号。接着用递归下降思路截取项和因子储存。
在函数求导方面,一样通过递归思路求导。求导的底层是常数或x^a,再层层返回组合成多项式。
在表达式化简方面我没有做过多尝试,只完成了0*和^1的化简。
在互测环节由于算法问题,对于多层的递归计算超时,需要优化算法减少时长。
Hack的方式主要是看对方识别求导的基本逻辑,以及输出+*等符号的考虑。
总结:
这三次作业反映出了我面对对象思想的薄弱,遇到问题还是习惯以面对过程的编程方式编程,对于继承接口的使用近乎为零,同时对于程序的测试考虑不全,代码冗余,还有许多需要改进的地方。