1.本章学习总结
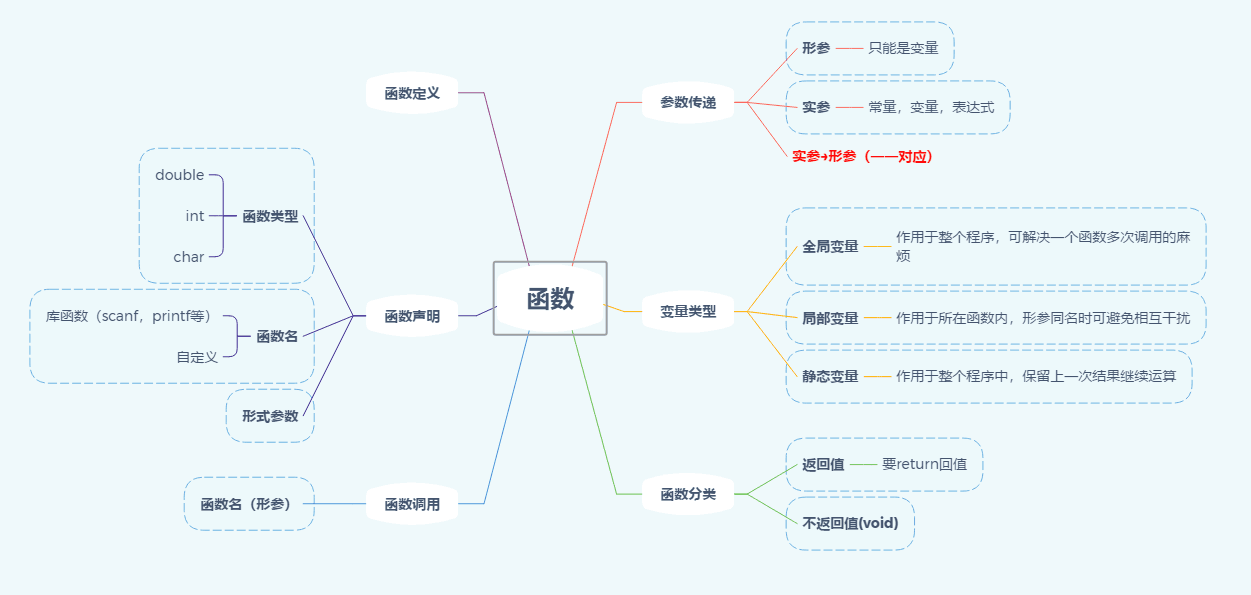
1.1 思维导图
1.2 本章学习体会及代码量学习体会
1.2.1 学习体会
本周函数的学习,说难也难,要知道**局部变量**,**全局变量**,**静态变量**的适用范围,有的时候,一不小心就会搞错。说简单也算简单,就是函数声明,定义和调用,运用函数就是使主函数中的代码看起来更清晰明了,而且,同样的函数类型可以多次调用,相比普通编程会更省事一些。
学习下来,觉得最大的收获就是知道函数里面可以多次调用函数,不用再次定义,很方便;而且,判断一个数m是不是完全平方数,时为了减少循环的时间,可以采用m=(int)sqrt(j)*(int)sqrt(j)这样的方式,既减少了代码量又大大缩短了运行时间。函数这一章,相比之前编程题还是有很多地方需要学习的,暑假自学的内容差不多要啃老啃完了,后面我得花更多时间在编程上,去学习新的知识了。
做大作业的时候,把程序写完是很容易,可是当你调试的时候会发现还有一大堆错误,运算符没有定义成随机生成,自己一直以为用getchar就可以,后来问同学才知道要定义一个函数表示,两步运算时每次产生的运算符都一样,应该用ch1,ch2来表示。在调用函数的时候,在形参前加了函数类型,一直编译错误。。。这次作业,本来打算完全靠自己做完的,后来各种错误简直让我崩溃,还是请教了大佬,加以指点,才顺利完成大作业。自己在做的时候,看过几个同学的代码,发现他们主函数里面全是函数调用,那样看起来很简明,于是自己也学着改成那样,发现这样代码要修改会方便很多。
总之,学无止境,多和他人交流,学习别人代码的长处,来不断优化自己的代码!
1.2.2 代码累计

2.PTA总分
2.1截图PTA中函数题目集的排名得分

2.2 我的总分:
函数题:145
3.PTA实验作业
3.1 PTA题目1
本题要求实现一个计算Fibonacci数的简单函数,并利用其实现另一个函数,输出两正整数m和n(0<m≤n≤10000)之间的所有Fibonacci数。所谓Fibonacci数列就是满足任一项数字是前两项的和(最开始两项均定义为1)的数列。
3.1.1 算法分析
定义fib函数返回第n项的斐波那契数
定义变量x1,x2,x分别表示相邻的三个斐波那契数
对相邻三个斐波那契数都赋初值为1,输出的项数小于3时,返回x的值也是正确的
for i=3 to n
x=x1+x2; //第三项是前两项的和
x1=x2; //将x2的值赋给x1,更新x1的值
x2=x; //将x的值赋给x2,更新x2的值
end for
return x; //将x的值返回到主函数中
定义PrintFN函数返回给定区间内的斐波那契数
定义count表示有没有斐波那契数,赋初值为0
定义i表示第i个斐波那契数,赋初值为1,J表示给定区间内的数
定义flag用来控制空格的输出情况
while(1) //找给定区间的斐波那契数,直到j>n时break跳出循环为止
j=fib(i) //从第一个斐波那契数开始找,看在不在给定区间
if(j>=m&&j<=n) //j在给定区间
if(flag==1)
printf(" ") //保证第一个斐波那契数前没有空格
count加1
printf("%d",j) //将符合的数输出
flag=1 //此时第一个斐波那契数已经输出,flag要赋值为1保证两个数之间有空格
end if
if(j>n) 如果条件成立,此时j已不在给定区间,需要退出循环,用break
i加1 将下一个斐波那契数的值赋给j
end while
if(count==0) 这个时候没有斐波那契数
输出 No Fibonacci number
3.1.2 代码截图


3.1.3 测试数据

3.1.4 PTA提交列表及说明

Q1:返回第n项的值时,当返回项数小于3的时候结果错误
A1:将x的初值也赋为1
Q2:无法返回斐波那契数
A2:再次调用第一个返回值的函数,并对其大小进行判断
4.大作业
题目:实现小学四则运算。
要求:
题目有3个难度级别,分别为:
第一级是1位数的一步加减乘除计算
第二级是2位数的2步加减运算
第三级是3位数的2步加减运算
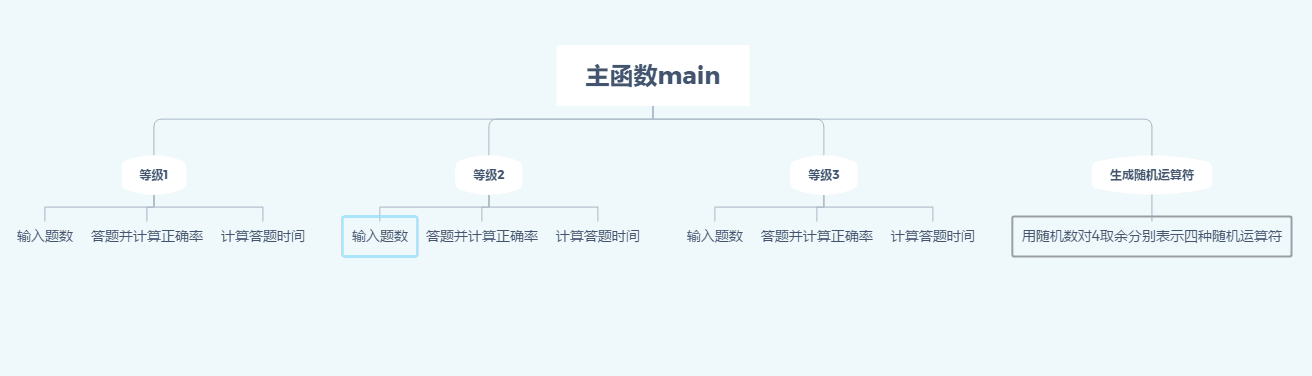
4.1.函数关系图
4.2.函数功能介绍
1.函数ch,产生随机运算符
用a表示随机数对4取余后得到的数字,分别对应4种情况,并将随机运算符分别赋予相应的ch,然后把ch结果返回
 。
。
2.函数main
开始先出现界面告诉答题者有三个等级可以选择,然后正确输出所要进入的等级后进入相应的函数调用,输入非法字符则提醒使用者并让其重新输入

3.定义等级函数
输入想要做的题目后进行循环做题,随机生成式子让用户输入结果,然后判断正误以及计算正确个数。同时,在开始做题的时候进行计时,结束的时候停止,计算出时间差,作为本次答题的时间

4.3 运行结果截图
按照程序功能,分别截图展示运行结果,对于临界、不合法数据,可单独截图运行结果图。
4.4 调试碰到问题及解决办法
Q1:每次得到的随机运算符都一样
A1:要用不同的ch,比如设为ch1,ch2来接收调用函数后得到的运算符,这样两步的时候就有+-号的不同
Q2:选择等级时输入非法字符,会连着输出两句提示错误的语句
A2:输入的空格也会被当成是输入的一个字符,属于非法运算符,所以会被输出两次,解决这个问题需要用getchar()将空格吸收掉,这样就可以正常输出了
4.5 大作业总结
此次作业,构思不难,可是细节处问题多多,同时,也让我知道自己还有许多不足,主要在以下几个方面我深有体会
- 1.当运算关系比较复杂的时候,主函数里面全部函数调用,函数定义放在主函数外面,那样看起来更直观。
- 2.先将主体思路构思好,再对局部代码进行优化。修改代码时,不要一出错就盲目地改正,那样只会越改越乱,最后自己都理不清思路
- 3.碰到新知识先自己去百度看看,不要一味问同学,经过自己看懂的知识点,才能印象更深刻。
- 4.体会到了程序员的不容易,设计四则运算只是一个很初级的游戏,都能有那么多的错误,那设计一个软件的程序所需要的代码量及会出现的错误是想都不用想的,肯定需要花大量时间去调试。同时,这也告诉我,做事要有耐心,有毅力。