hiho一下 第四十二周

题目1 : 骨牌覆盖问题·二

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

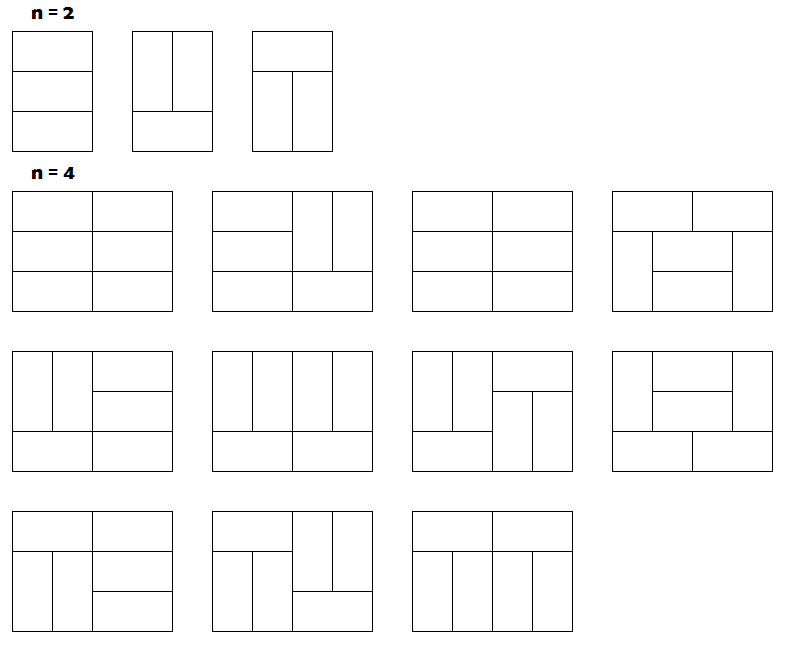
上一周我们研究了2xN的骨牌问题，这一周我们不妨加大一下难度，研究一下3xN的骨牌问题？
所以我们的题目是：对于3xN的棋盘，使用1x2的骨牌去覆盖一共有多少种不同的覆盖方法呢？
首先我们可以肯定，奇数长度一定是没有办法覆盖的；对于偶数长度，比如2，4，我们有下面几种覆盖方式：

提示：3xN骨牌覆盖

输入

第1行：1个整数N。表示棋盘长度。1≤N≤100,000,000

输出

第1行：1个整数，表示覆盖方案数 MOD 12357

样例输入

62247088

样例输出

4037

题目画错了,n=4的解是11，图中有两个相同的图案。
解法：n等于奇数结果是0，这里求偶数间的递推公式，i表示第i个偶数；
观测n=4的图可以发现a[i+1]=3*a[i]+2*a[i-1]+2*a[i-2]+.....+a[0];
由此可以得到a[i+1]=4*a[i]-a[i-1];初值a[0]=1,a[1]=3;
再使用矩阵的n方的的加速算法可得解；O(log(n)).

#include <cstdio>
#include <cstring>
int n;
const int mod = 12357;
long long a[2][2],b[2][2],c[2][2];
int main(){
   a[0][0]=4;a[0][1]=12356;a[1][0]=1;
   b[0][0]=1;b[1][1]=1;
   scanf("%d",&n);
   if(n&1){
       printf("0\n");
       return 0;
   }
   n>>=1;
   while(n){
       if(n&1){
           memcpy(c,b,sizeof(b));
           b[0][0]=(c[0][0]*a[0][0]+c[0][1]*a[1][0])%mod;
           b[0][1]=(c[0][0]*a[0][1]+c[0][1]*a[1][1])%mod;
           b[1][1]=(c[1][0]*a[0][1]+c[1][1]*a[1][1])%mod;
           b[1][0]=(c[1][0]*a[0][0]+c[1][1]*a[1][0])%mod;
       }
       memcpy(c,a,sizeof(a));
       a[0][0]=(c[0][0]*c[0][0]+c[0][1]*c[1][0])%mod;
       a[0][1]=(c[0][0]*c[0][1]+c[0][1]*c[1][1])%mod;
       a[1][1]=(c[1][0]*c[0][1]+c[1][1]*c[1][1])%mod;
       a[1][0]=(c[1][0]*c[0][0]+c[1][1]*c[1][0])%mod;
       n>>=1;
   }
   printf("%d\n",(b[1][0]*3+b[1][1])%mod);
   return 0;
}