等式约束优化
当目标函数加上约束条件之后,问题就变成如下形式:
目标函数和约束
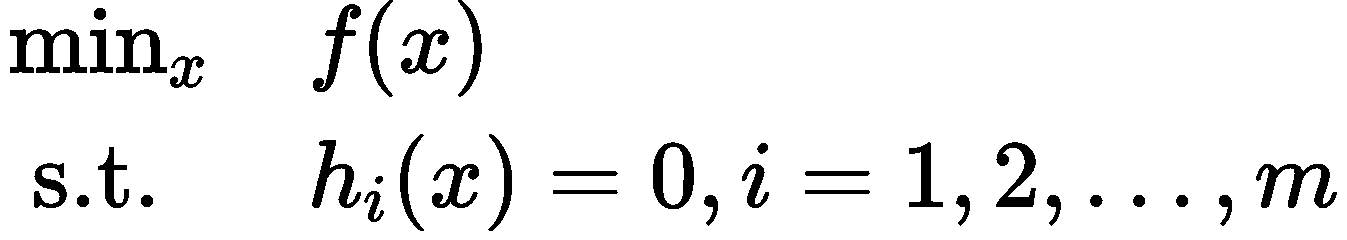
约束条件会将解的范围限定在一个可行域,此时不一定能找到使得 ∇xf(x)为 0 的点,只需找到在可行域内使得 f(x) 最小的值即可,常用的方法即为拉格朗日乘子法,该方法首先引入 Lagrange Multiplier α∈Rm ,构建 Lagrangian 如下: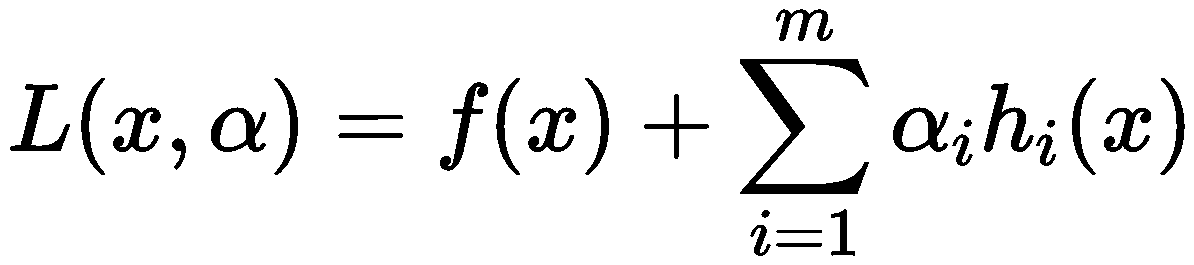
求解方法如下:首先对 Lagrangian 关于 α 与 x 求 :
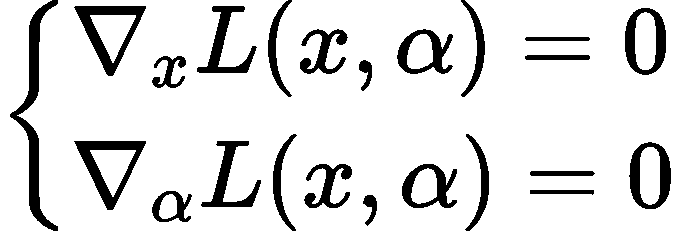
令导数为 0 ,求得 x 、α 的值后,将 x 带入 f(x)即为在约束条件 hi(x)下的可行解。这样做的意义是什么呢?
接下来看一个直观的示例,对于二维情况下的目标函数是 f(x,y),在平面中画出 f(x,y) 的等高线,如下图的虚线所示, 并只给出一个约束等式 h(x,y)=0 ,如下图的绿线所示,目标函数 f(x,y)与约束 g(x,y) 只有三种情况,相交、相切或者没有交集,没交集肯定不是解,只有相交或者相切可能是解,但相交得到的一定不是最优值,因为相交意味着肯定还存在其它的等高线在该条等高线的内部或者外部,使得新的等高线与目标函数的交点的值更大或者更小,这就意味着只有等高线与目标函数的曲线相切的时候,才可能得到可行解。
因此给出结论:拉格朗日乘子法取得极值的必要条件是目标函数与约束函数相切,这时两者的法向量是平行的(这里是只有一个约束情况),即
![]()
所以只要满足上述等式,且满足之前的约束 hi(x)=0,i=1,2,…,m,即可得到解,联立起来,正好得到就是拉格朗日乘子法。
这里只是直观展示了一下拉格朗日乘子法的几何推导 ,并没有给出详细的证明。
当约束有多个时
用向量语言来表述就是:如果条件极值点 存在,那么在该点处,目标函数的改进方向
必然落在
个约束函数在该点处法向量
张成的线性子空间内。
注意:这里最终求得的解可能有多个,不是所有的解都会使目标函数达到最小,只可能有一个解。
而这里得到多个解,是因为在这些解处满足约束函数且目标函数的改进方向 必然落在
个约束函数在该点处法向量
张成的线性子空间内
多个解带入目标函数,看哪个解使目标函数最小,则该解就位最优解
下面举例说明一下:
约束只有一个的情况:
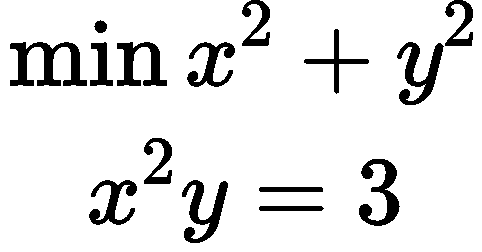
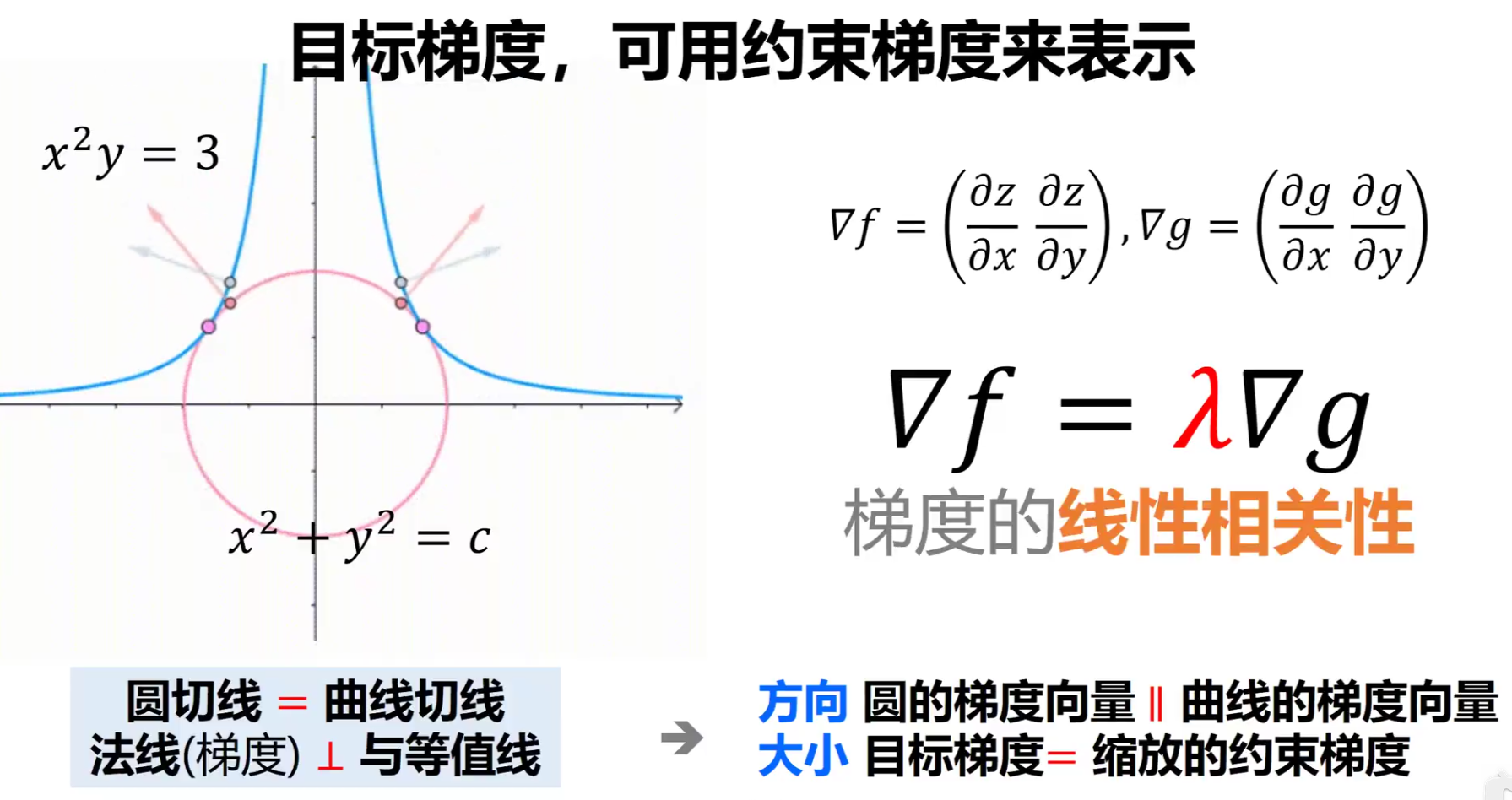
h(x) = x² + y² 的等值线
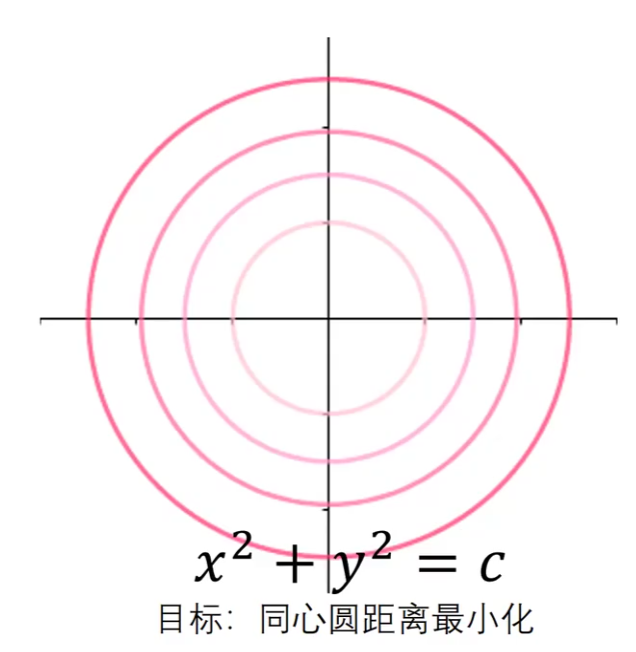
g(x)= x² y 的等值线
蓝线表示g(x)= 3的等值线,此时x与y的对应关系一一对应
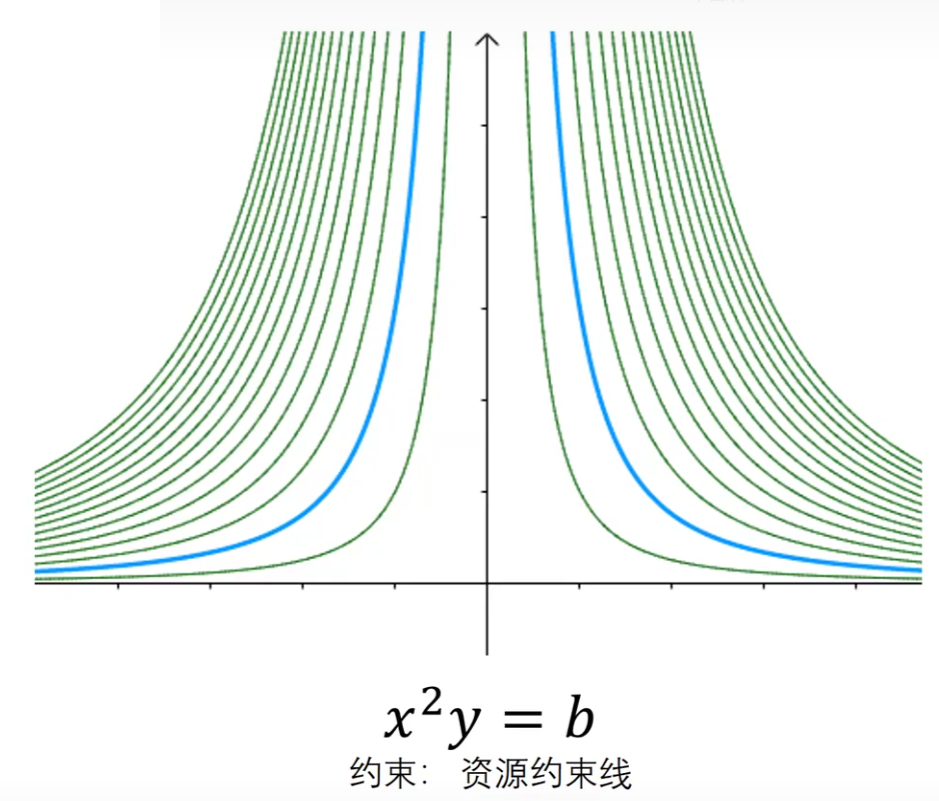
h(x)=x² + y² 的等值线有内到外逐渐增加,当增加的等值线与约束线g(x)= 3线切时,h(x)最小
因为根据下图可已看出,h(x)等值线再往外扩与g(x)有交点,但h(x)的值变大。

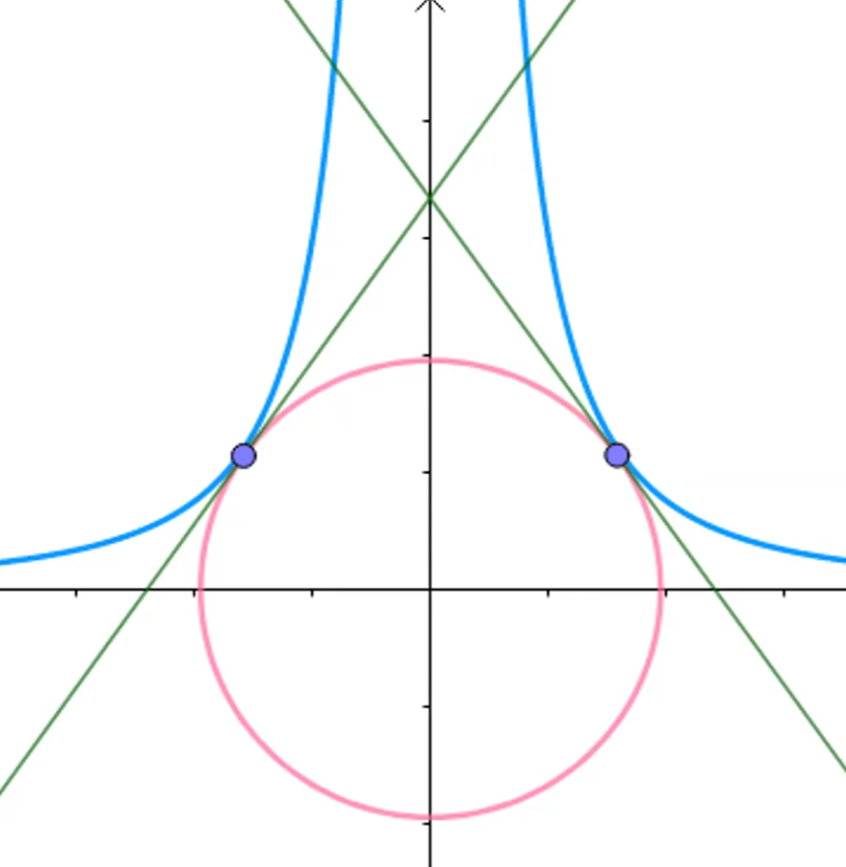
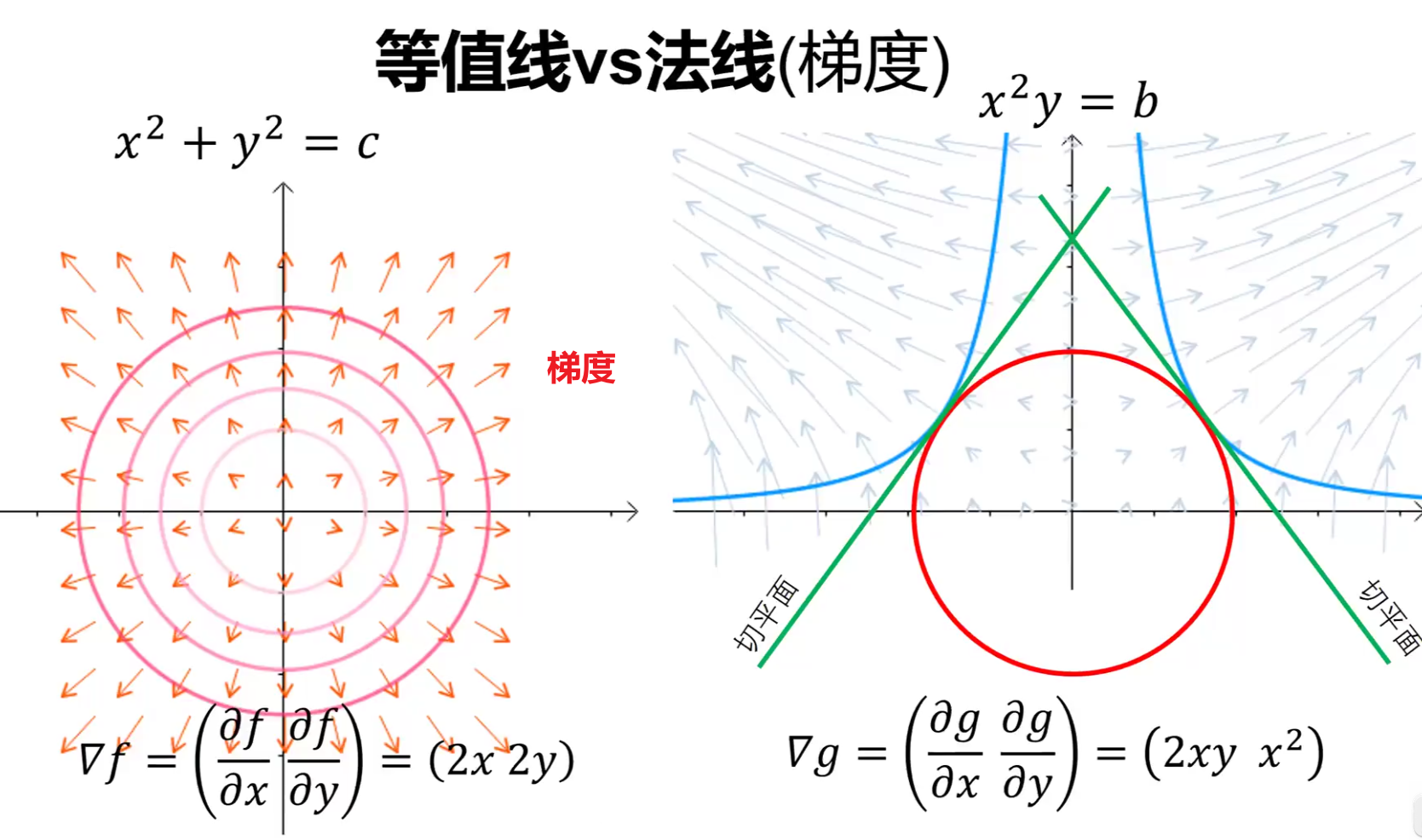
可以得到在切点处目标函数的梯度与约束的梯度平行
当约束有多个时,在符合条件的点处,目标函数的梯度为约束梯度的线性组合
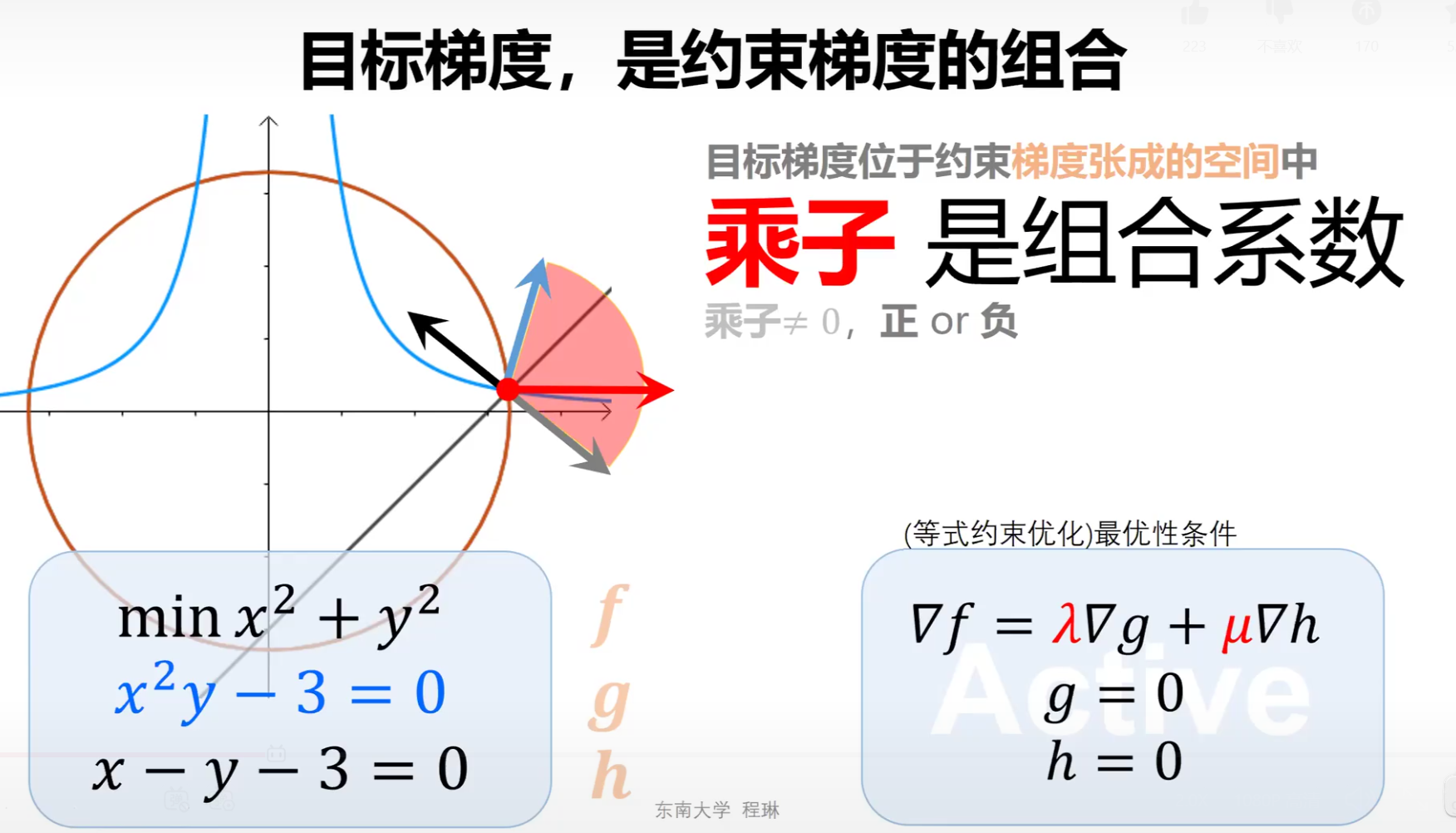
下面求解一个等式约束的问题


