1 三次B样条曲线方程
B样条曲线分为近似拟合和插值拟合，所谓近似拟合就是不过特征点，而插值拟合就是通过特征点，但是插值拟合需要经过反算得到控制点再拟合出过特征点的B样条曲线方程。这里会一次介绍两种拟合算法。首先介绍B样条的曲线方程。
B样条曲线的总方程为：
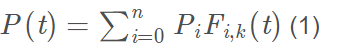
其中P i 是控制曲线的特征点，Fi,k(u)则是K阶B样条基函数。
1.1 三次B样条曲线方程中基函数为：
其中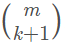 
表示阶乘。化成看的明白的式子就是（以四个控制点为例）：
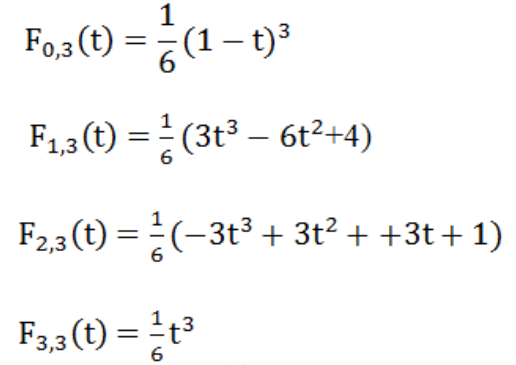
将图片上的基函数代入到方程（1）中，就是：
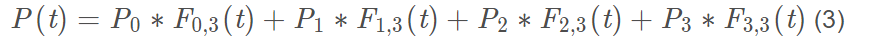
方程（3）就是三次B样条曲线方程。上式(2)的j是什么意思，其实j就是控制点的索引值。这里我把书上的公式摘抄下来，可能看起来更为清晰。参考书籍：《计算机图形学 第3版》何援军 第13章
三次B样条曲线计算
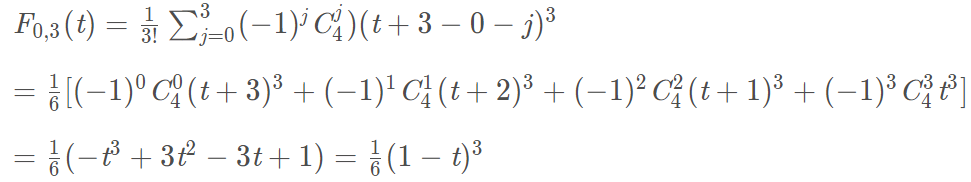
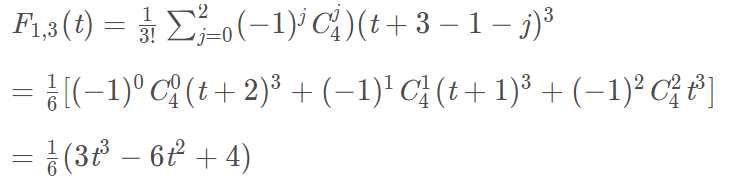
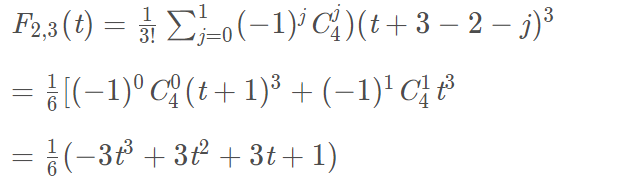
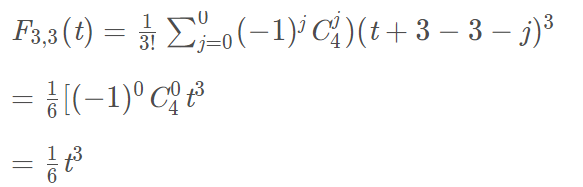
2 三次B样条曲线近似拟合
近似拟合很简单。不需要求控制点，求得
， 由上述方程（3），代入
，就可以得到由这四个点近似拟合的一段三次B样条曲线，起始点在P 0，终点在P 1，对于闭合轮廓，最后一段可以取前两点做辅助，拟合实验结果我最后一块给出。这种近似拟合曲线光滑，但是最大不足就是不过特征点，也就是不过P i ，需要过点需要反求控制点再拟合。
3 三次B样条插值拟合
插值拟合较为复杂。其实也不算是很复杂，找资料过程和理解过程是一个复杂的过程。不过有了前面大神做工作，我们只是借用别人的成果写代码就好了。我给大家看一篇论文，大家可以百度或者去知网搜索，闭合 B 样条曲线控制点的快速求解算法及应用。文章讲解了反求控制点的具体步骤，写的非常详细，基本上贴近代码的那种。大家可以根据这篇论文反求控制点，拟合出来的三次B样条曲线是经过P i 。代码就不放了，很多，可以根据我给的那篇论文直接编写相应代码，有问题可以私信我，知无不言。
4 拟合结果
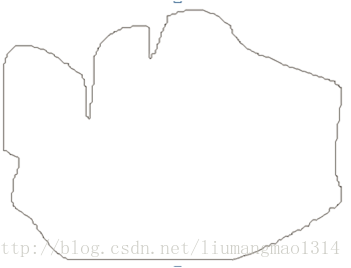
原轮廓
近似拟合轮廓。可以看到没过黑色特征点，只是近似拟合
插值拟。可以看到曲线经过黑色特征点，不过有一些不足之处。
5 总结
三次B样条曲线拟合轮廓效果还是可以，较之Beizer（可以参考我博客三次Beizer曲线拟合算法），B样条将一些细节描述的很好，很多细节之处都贴近原轮廓，但是有一些不足之处，可以看到对直线拟合效果不是很好。两篇博客都是关于闭合轮廓的拟合，对于非闭合或者只是一段曲线拟合，还有一种曲线是很好的，《数值分析》提到过，叫三次样条插值拟合，拟合效果很好，我做过拟合一元三次方程曲线，拟合效果跟原曲线非常贴近，不过过程中需要用到追赶法，而追赶法需要满足一个条件，对于闭合曲线三次样条插值是不满足这个条件的，所以我没去深研究，大家可以去试一试。谢谢大家！
原文链接：https://blog.csdn.net/liumangmao1314/article/details/54588155