MATLAB quadprog函数参数介绍

                

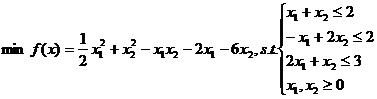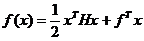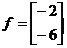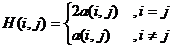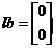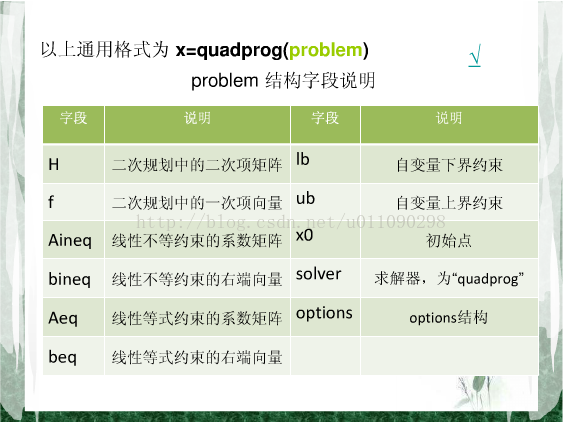
【例】求如下二次规划问题。

        【分析】首先应该把目标函数表示成如下矩阵形式：

        这里要细说一下如何写成矩阵形式。

        首先，向量x是很容易写出的，因为f(x)包含两个变量x₁和x₂，因此

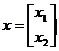
        其次，向量f只与两个变量x₁和x₂的一次项有关，所以f^Tx=-2x₁-6x₂，因此

        最后，矩阵H只与两个变量x₁和x₂的二次项有关，所以，这里要注意的是不同于二次型，这里有个系数1/2，所以矩阵H的元素是二次型中的矩阵元素大小的两倍。给出一个规律：设矩阵H第i行第j列的元素大小为H(i,j)，二次项x_ix_j的系数为a(i,j)，则

        本例中，，这是由于x₁的平方项（即x₁x₁）系数为1/2，所以第1行第1列的元素为1=2*(1/2)，x₂的平方项（即x₂x₂）系数为1，所以第2行第2列的元素为2=2*1，x₁x₂项（即x₂x₁）的系数为-1，所以第1行第2列和第2行第1列的元素均为-1。

        目标函数搞定之后，下面来看约束条件部分，约束条件应该写成如下形式：

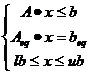
        本例中约束条件只有不等式约束，因此A_eq和b_eq为空，对于A和b很容易就可以得出来：

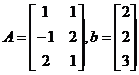
        而约束条件中对变量x₁和x₂只给出下限，没有给上限，因此ub为空，

        得到了所有的参数，将参数输入MATLAB，编程如下：（代码是直接在Command Window中一行一行录入的，所以每行前面有符号“>>”）

>> H = [1 -1; -1 2];
>> f = [-2; -6];
>> A = [1 1; -1 2; 2 1];
>> b = [2; 2; 3];
>> lb = [0; 0];
>> [x,fval,exitflag,output,lambda] = quadprog(H,f,A,b,[],[],lb)

   输出以下结果：

Warning: Large-scale algorithm does not currently solve this problem formulation,
using medium-scale algorithm instead. 
> In quadprog at 291
Optimization terminated.

x =

    0.6667
    1.3333

fval =

   -8.2222

exitflag =

     1

output = 

         iterations: 3
    constrviolation: 0
          algorithm: 'medium-scale: active-set'
      firstorderopt: []
       cgiterations: []
            message: 'Optimization terminated.'

lambda = 

      lower: [2x1 double]
      upper: [2x1 double]
      eqlin: [0x1 double]
    ineqlin: [3x1 double]

参考文献：

【1】孙文瑜, 徐成贤,朱德通.最优化方法(第二版)[M]. 北京:高等教育出版社, 2010.

【2】龚纯，王正林. 精通MATLAB最优化计算[M].北京: 电子工业出版社,2009.

【3】lnsunqingshen, 464518439.什么是凸二次规划, 百度知道，2011-06-20.

【4】李明强.几类特殊凸二次规划问题的求解算法研究[D].山东科技大学,2013 .

【5】于绍慧.边界约束凸二次规划的求解[D].南京航空航天大学,2005.

参考：https://blog.csdn.net/jbb0523/article/details/50598641

https://blog.csdn.net/tianzy16/article/details/87916128