我在RSA学习总结的第三部分关于Mille-Rabin素数测试的正确性证明里需要用到此定理,由于证明太长,故另开一章于此。(为啥我说话突然文绉绉了Orz,可能是这周辩论打多了)
结论是对素数p,modulo p的原根存在,个数为与ø(p-1),modulo p2的原根个数为(p-1)ø(p-1)个
对奇素数p,modulo p^n的原根存在,个数为pn-2(p-1)ø(p-1) (n>=3)
首先证明对任意素数p,modulo p的原根存在
以下是证明思路(符号的意思在第二张图,完整证明里有)
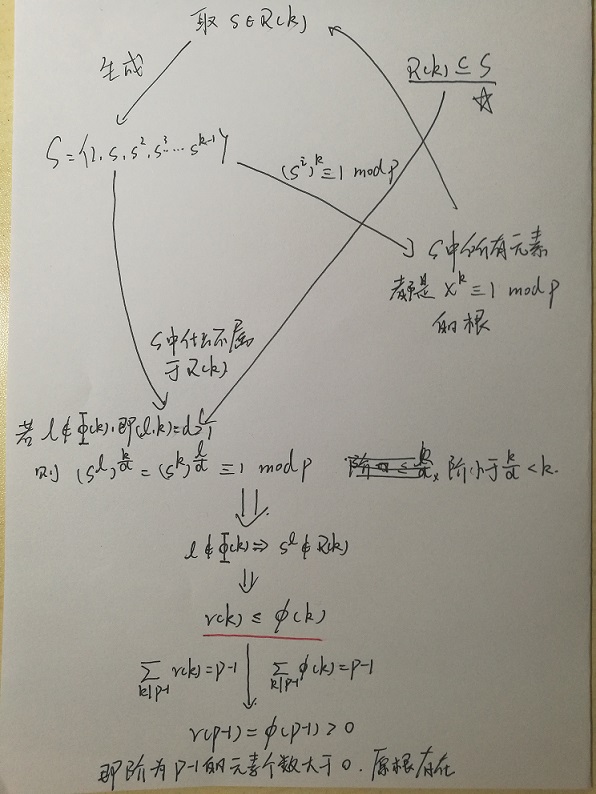


知道了modulo p^2下Primitive root存在后可以推广至p^n
