国际照明委员会(CIE)于1931年推荐的标准色度观察者光谱三刺激值函数及相应的色品图、标准照明体与标准光源作为CIE标准色度系统,至今仍在许多方面得到广泛的应用,使人们可以在统一的基准下进行颜色的计量测试和比较分析,并具有了学术和生产交流的色彩专用语言,促进了颜色科学和相关产业的进步和发展。但是,在CIE1931标准色度系统的实际应用中发现了一些不足之处,尤其是色品图的不均匀性即各色区中颜色感知差异的容限大小不等,这在实用中产生了较大的问题。此外,工业应用中还常常需要比较和评价不同亮度等级的颜色,而这些问题的出现推动了均匀颜色空间以及颜色差异计算方法的研究。
一、均匀色品图
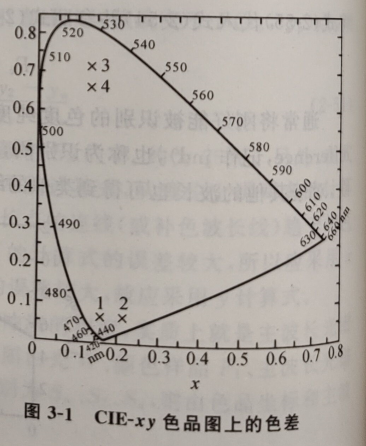
定量地表示颜色感知差别的量称为色差(color difference) ,可是用CIE-xy色品图上的距离来求出的色差却是不均匀的。如图3-1所示的CIE色品图上有两组处于不同色区的颜色对,其中第一对颜色1和2在蓝色区,第二对颜色3和4在绿色区,并且假定在该色品图上1和2之间的距离与3和4之间的距离相等,这时按常规思维因距离相等就应认为感知上的颜色差异也相同,但实际上随着在色品图上所处的位置不同其,感知有相当的差别。可见,对于相同的色距离有时出现较大的感知上的差异,有时又呈现出难以分辨的很小的感知差别,这显然是很不合理的,无法满足工业应用的需求。为了定量地表示色差,需要对人眼的颜色分辨能力进行测试和分析。颜色是三维量,包括明度和色品(如色调、彩度或饱和度等),因此对颜色分辨力的研究有必要分别从：1、光亮度分辨力2、波长和色纯度的分辨力3、色品的分辨力这几个方面来探讨。
对此在学术界麦克亚当等人的实验数据验证下，CIE先后推出了CIE1960 UCS（2°和10°视场）、CIE1976 UCS的 （相对）均匀色品图。
二、均匀明度标尺
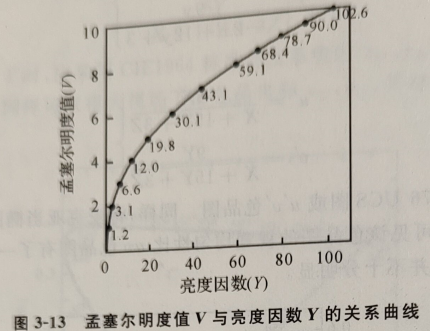
上面介绍的均匀色品图只涉及颜色的色品,包括色调和饱和度,因而还需要研究颜色的第三维特性即明度的均匀性问题。明度表示颜色的明亮程度,大体上与三刺激值中的Y相对应。物体色的Y也称为亮度因数,即在规定的光照条件下和给定的方向上,物体表面的亮度与同一光照下完全漫反射体的亮度之比。但是,对于视觉相同的明度等级其所对应的Y值却是非等间隔的,反之亦然,即如将Y作10,20,30,….变化时,对应的明度也不是均匀增加的。因此,为使明度变得均匀而将亮度因数Y进行修正后的标尺称为均匀明度标尺(uniform lightness scale, ULS)。孟塞尔颜色系统提供了很好的均匀明度标尺,这是因为孟塞尔颜色系统的明度即孟塞尔明度值V在视觉上是均匀的。孟塞尔颜色系统将明度值V分为0~10共十一个等级,其中0为理想黑色,10为理想白色,并且V值越大表示视知觉的明亮度越高。由孟塞尔色卡的亮度因数Y向孟塞尔明度值V的转换式为：Y=1.2219V - 0.23111V2 + 0.23951V3—0.021009V4+0.0008404V5。可见,两者之间存在明显的非线性关系,其对应的关系曲线如下图所示,图中曲线上的数字为各点的Y值。由图可知,在黑色附近非线性尤其明显,所以在黑色中色就会明显变白。
由Y值向均匀明度标尺的变换除了上述的孟塞尔明度值函数以外,还有其他多种转换方法,如平方根公式、CIE明度指数函数、德国DIN系统明度标尺等。
三、均匀颜色空间
上面讨论的均匀色品图中并未涉及有关颜色的明度均匀性,即使采用(u',v', Y)代替(x, y, Y),色品坐标的均匀性提高了,但明度的均匀性没有变化。因此,应考虑将均匀色品标尺和均匀明度标尺组合起来,形成一个均匀的三维空间,称之为均匀颜色空间(uniform color space),同时,把在均匀颜色空间中对应于明度的坐标称为明度指数(psychometriclightness).
3.1、CIE1964均匀颜色空间
国际照明委员会基于威泽斯基(Wyszecki)提出的利用CIE1960 UCS图的均匀颜色空间,于1964年推荐了CIE1964 W*U*V颜色空间。该系统采用三个参数即明度指数W*、色品指数U*和V*来表示颜色,并由此组合的三维坐标形成了颜色的立体空间,它们的计算公式为：
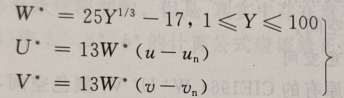
式中,u、v是颜色样品的CIE1960色品坐标,而un、vn是照明光源的色品坐标。可见,明度指数W*与刺激值Y有关,并且明度指数标尺在知觉上是均匀的,即每一个单位量的差别代表相等的知觉差异,因而它更准确地表达了颜色明度的变化;色品指数U*和V*的计算式是基于CIE1960 UCS图的u、v色品坐标,同时又考虑了明度指数W*对色品坐标的影响,故当明度指数W*增大或减小时色品指数也随之增大或减小。
在该均匀颜色空间中,两个颜色(U1* ,V1* ,W1* )和(U2* ,V2* ,W2*)之间的色差为：
， 式中的色差ΔE=1时称为1个NBS色差单位。NBS ( National Bureau of Standard)色差单位原是由1942年亨特的均匀颜色空间推导出的色差公式所决定的,而CIE1964均匀颜色空间的色差公式推导出的色差单位正好与它的单位一致。不同的色差公式导出的色差单位不同,故在计算色差时必须注明是按何种色差公式计算的。对于有色产品的色差允许范围,应根据具体情况分别设定,如涂料的颜色稍有差别就比较明显,故色差可以定为小于1个NBS单位,纺织品通常定为小于2个NBS单位,而彩色电视可以取4～5个NBS色差单位。
3.2、CIE1976 L*u*v*均匀颜色空间
国际照明委员会改进了原有的CIE1964 W*U*V*颜色空间,提出采用L*、u*、v*作为三维直角坐标的CIE1976 L*u*v*颜色空间,也称为CIELUV颜色空间,它主要用于如电视工业等加混色(additive mixture)的表示和评价。在该空间中,L*为明度,u*、v*表示颜色的色品坐标,其计算公式为：
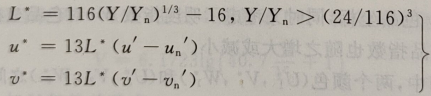
式中,u、v是颜色样品的CIE1976色品坐标,而un、vn是照明光源的色品坐标。
3.3、CIE1976 L*a*b*均匀颜色空间
国际照明委员会改进了原有的CIE1964 W*U*V*颜色空间,提出采用L*、u*、v*作为三维直角坐标的CIE1976 L*u*v*颜色空间,也称为CIELUV颜色空间,它主要用于如电视工业等加混色(additive mixture)的表示和评价。在该空间中,L*为明度,u*、v*表示颜色的色品坐标,其计算公式为：
式中,X、Y、Z为颜色样品的三刺激值,Xn、Yn、Zn为CIE标准照明体照射在完全漫反射体上,然后反射到观察者眼中的三刺激值,其中Yn=100。
四、色差及其的评价
4.1、色差与心理相关量
在CIELUV和CIELAB颜色空间中,以两个被比较颜色点的欧氏距离表示色差,同时还各有一组与心理量近似对应的感知属性,即明度、彩度、色调角及色调差。下面分别具体介绍这些颜色评价参数,并以下标"uv"和"ab"来区分CIELUV和CIELAB颜色空间。
色差：
明度：
彩度：
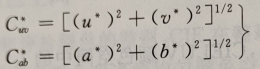
色调角：
色调差：
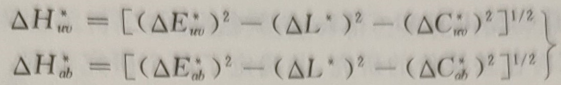
4.2、色差的视觉判断
对于两个颜色之间差别的视觉判断主要有两种直观的评价,即可感知性(perceptibility)和可接受性(acceptability),可感知性是指观察者能够看到颜色的差别或能够判断两个颜色样品之间色差的大小的视觉属性,而可接受性则表示观察者是否认为可以接受被观察颜色差别的视觉判断。但是,目视比较和判断具有较大的主观性和易变性,在工业生产中不宜直接作为颜色质量的评价依据。因此,仪器测色显得尤为重要,但是物理测量的数据应该能预测观察者所看到的情况,并需要有合适的色差公式使之计算出来的色差能够预测目视色差。可见,为了实现色差的符合视觉判断的客观评价,需要建立能够预测可感知性判断的色差方程,而色差方程的建立是基于大量的颜色视觉判断和色差比较心理物理实验数据之上的,同时还要考虑颜色刺激的时间与空间特性和视觉实验的观察条件等因素。
4.3、色差公式
理想的色差评价模型应基于真正视觉感知均匀的颜色空间，其预测的色差应与目视判断具有良好的一致性，而且可以采用统一的色差宽容度来进行颜色质量控制,即对所有颜色产品能用相同的色差容限来判定其合格与否,而与标准色样在颜色空间中所处的位置或所属的色区无关。这是色差研究的最终目标,是一项十分困难和艰巨的任务。长期以来,各国的颜色科学工作者已在这一领域投入了大量的精力,做了很多的工作,至今已提出几十个色差公式,其中一些公式已被CIE阶段性地推荐为评价标准。
纵观色差评价研究的发展,以CIE1976均匀颜色空间为界,现有的色差公式大致可以分为1976年以前发表的早期色差公式，如：瑞利立方根色差公式、FMC-I公式、FMC-II公式、ANLAB公式以及亨特Lab公式等。1976年以来发表的近期色差公式有：ECM色差公式、JPC79色差公式、CMC（l:c）色差公式、BFD（l:c）色差公式、CIELAB色差公式的加权式、CIE94以及CIEDE2000色差公式等。
五、一维颜色标尺
颜色是三维量,包括明度、色调、彩度或饱和度,但其中任何一个标尺又可用来描述有色物体的单一性能,如从无色经过黄色到橙色或红色的物体着色成分的变化就可以用色调标尺来表示。这种一维的颜色标尺在有些情况下具有特定应用意义,如白布、白塑料等白色的物体,可以用白度标尺来描述和评价其白色的程度;当将白色物体长期置于阳光下曝晒时,白色会逐渐变黄,这时可用黄度来描述这种稍带有黄色的白色物体,而白色物体经过一段时间后变黄的程度则可用变黄度表示。
5.1、黄度标尺
在几乎全是白色的样品中,往往会有黄色的出现,令人不悦,因此人们投入大量的精力来建立均匀黄度标尺。美国ASTM (American Society of Testing Materials)标准采纳了以CIE1931标准色度观察者和CIE标准照明体的色度参数为基础而得到的黄度标尺,该标尺只与看起来是黄色或蓝色的视觉感知有关,其中视觉蓝色的情况下其黄度指数为负数,并且它们,都不能用来描述视觉上偏红或偏绿的颜色。由标准照明体C和CIE1931标准色度观察者获得颜色样品的三刺激值X、Y、Z,以此可以进一步计算出样品的黄度指数YI,即
白色的样品在特定的条件下随时间逐渐变黄的程度通常采用変黃度指数ΔYI来描述,它可由样品变黄前的黄度YI0和变黄后的黄度YI计算出来:
5.2、白度标尺
白色是在人们的日常生活中十分普遍的一种颜色,也是相关工业产品如纺织品、纸张、涂料、塑料制品等的一个大类,具有重要的意义。在荧光增白剂出现以前,白度的提高是通过对材质进行漂白并加点蓝或通过优选和纯化材质来达到。通常,接近完全漫射体的氧化镁和硫酸钡可以认为是理想的白色,而某些材料在添加了荧光增白剂以后,其白度可超过完全漫射体，这给白度的评价增加了复杂性。
与红、绿、黄、蓝等其他颜色一样、白色也可以用CIE标准色度系统进行数字化描述。有色品图上,白色只占有沿着570mm和470nm为主波长下很狭窄的区域,在颜色空间中,白色都处于围绕无彩明度轴上端的范围,沿着无彩轴向下增加其灰度则白色将逐渐变为灰色,而沿着彩度增加的径向其白色将渐变为各种彩色。常见的白度公式有：单波段白度公式、多波段白度公式、以明度L和色纯度表示的白度公式、与色彩概念有关的白度公式、CIE白度公式等，这里不做详细阐述，感兴趣的可自行查阅。
六、同色异谱颜色及其评价
由格拉斯曼颜色混合定律可知,两种光谱分布不同的光刺激其颜色外貌可能完全相匹配,这种情况就称为同色异谱(metamerism)现象。在工业生产实践中,特别是如印染、印刷、油漆、绘画、彩色摄影、彩色电视等行业中,经常会遇到同色异谱现象,所以这是在颜色科学中的一个重要问题。
在某种确定的照明与测量条件下,非荧光性的材料所显示的颜色主要取决于材料本身的光度特性,所以当两种非荧光性材料的光度特性完全一致时,它们在同样的照明和观察条件下具有相同的颜色,这是毫无疑问的。但是,如果这两种非荧光性材料的光度特性不完全一致,,那么它们必须在某一特定的照明和观察条件下才有可能具有相同的颜色外貌。因此,当两种颜色样品的光谱反射比或光谱透射比不同(异谱),而在特定的照明和观察条件下其颜色外貌又能相互匹配(同色)的两种颜色刺激就称为同色异谱颜色或同色异谱色对(metameric pair)。
通常,同色异谱颜色的三刺激值分别相等,即
式中,Ψ1(λ)和Ψ2(λ)表示两个不同的颜色刺激。一般讨论的同色异谱颜色常常是指在同样的照明和观察条件(包括照明体的相对光谱功率分布、观察者的色匹配函数以及观察视场等)下两个具有不同光度特性的颜色具有同样的颜色外貌。这时,如果改变照明体或者观察者,那么颜色的匹配就会被破坏或称为失配,因此CIE对因条件变化所产生的同色异谱色的失配推荐了改变照明体光谱分布和改变观察者色匹配函数的评价方法。
同色异谱颜色在工业领域中具有重要的应用意义。在实际生产中,常常需要复现某种颜色,如纺织印染的颜色匹配是最典型的例子之一,这时要求再现的颜色样品在某个选定的照明体下与标准色样的颜色外貌相同,可是在具体的颜色复现过程中很难做到复制色样与标样的配方和染料特性完全相同,更不用说是异质媒介的颜色复制了,所以在这样的情形下就需要对这两种颜色样品进行同色异谱程度的评价。此外，同色异谱颜色的分析和评价内容这里不做赘述，可自行学习。
七、光源显色性的评价
对光源颜色特性的评价主要有两个方面的内容:一方面是人眼直接观察光源时所看到的颜色,其评价方法与物体色类似,可以通过计算其三刺激值和相关色温来捕述光源本身的颜色；另一方面就是物体在光源照明下所呈现的颜色效果,研究照明光源对物体颜色的影响及其评价方法,即光源的显色性问题。
人们通常习惯地把物体在日光下所呈现的颜色认为是其真实颜色。同时,由于白炽灯的,发光特性与黑体比较接近,所以在它的照明下人眼也能感受到物体的真实颜色。但是,很多人工光源的特性并不完全与日光或白炽灯的特性相同,而且它们还各具有不同的色温,所以在应用人工光源照明时,需要一种检验方法来评价采用人工光源与日光或白炽灯照明同一种物体时的差别及其程度。
7.1、光源显色性
通常把照明光源对物体色外貌所产生的影响称为显色(color rendering) ,而将光源固有的显色特性称为显色性(color rendering property)。光源的光谱分布决定了光源的显色性,具有连续光谱分布的光源均有较好的显色性,如日光、白炽灯等。另外,由特定的色光组成的混合光源也能有很好的显色性,如波长为450nm(蓝),540nm(绿)和610nm(橙)的光谱辐射对提高光源的显色性具有特殊的效果,所以采用这三种色光以适当的比例混合所产生的白光与连续光谱的日光或白炽灯具有同样优良的显色性。此外,光源的色温和显色性之间没有必然的联系,因为具有不同光谱分布的光源可能有相同的色温,但是其显色性可能差别很大。光源的显色性影响人眼所观察的物体颜色,显色性好的光源照明下物体颜色的失真就小,所以与物体表面色相关的工业领域如纺织、印染、涂料、印刷、彩色摄影、彩色电视等必须考虑光源显色性对颜色复制及其评价的影响。为了比较光源显色性的优劣,有必要建立定量的评价方法。显色性的评价方法大体上可分为两种,即基于光谱分布之差的方法和基于作为标准的物体色(试验色)外貌之差别的方法。目前,在光源显色性评价上多采用后一种方法,本节也将说明作为试验色方法代表的CIE于1974年推荐的光源显色性评价方法。对光源显色性进行定量的评价是光源制造工业评价光源质量的一个重要方面,还可为提高照明质量、改进光源的特性提供必要的技术参数。
关于光源显色性的计算这里不做介绍，一般来说光源显色性越高越好。