图的邻接矩阵:图的邻接矩阵存储方式是用两个数组表示图。一个一维数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储图中边或弧的信息。如下图所示:
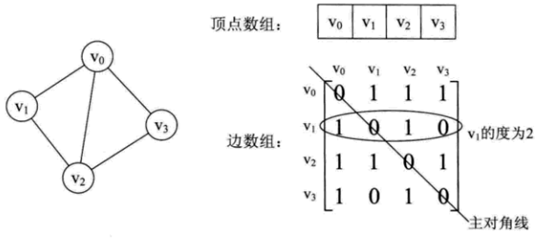
无向图的边数组是一个对称矩阵。有向图矩阵不对称。
图的遍历:深度优先更适合目标比较明确,以找到目标为主要目的情况,而广度优先更适合在不断扩大遍历范围时找到相对最优的情况。
在网图和非网图中,最短路径的含义是不同的。由于非网图它没有边上的权值,所谓的最短路径,其实就是指两个顶点之间经过的边数最少的路径;而对于网图来说,最短路径,是指两定点之间经过的边上权值之和最少的路径,并且我们称路径上的第一个顶点是源点,最后一个顶点是终点。显然,我们研究网图更有实际意义。
迪杰斯特拉算法并不是一下子求出源点到终点的最短路径,而是一步步求出他们之间顶点的最短路径,过程中都是基于已经求出的最短路径的基础上,球的更远顶点的最短路径,最终得到你要的结果。
对AOV网进行拓扑排序的基本思路是:从AOV网中选择一个入度为0的顶点输出,然后删去此顶点,并删除以此顶点为尾的弧,继续重复此步骤,直到输出全部定点或者AOV网中不存在入度为0的顶点为止。
在AOV网中,我们把路径上各个活动所持续的时间之和称为路径长度,从源点到汇点具有最大长度的路径叫做关键路径,在关键路径上的活动叫做关键活动。
总结:图的存储结构我们一共讲了五种,如下图所示:

其中比较重要的是邻接矩阵和邻接表,他们分别代表着边集是用数组还是链表的方式存储。十字链表是邻接矩阵的一种升级,而临界多重表则是邻接表的升级。边集数组更多考虑的是对边的关注。用什么存储结构需要具体问题具体分析,通常稠密图,或读存数据较多,结构修改较少的图,用临界矩阵要更合适,反之应该考虑邻接表。
图的遍历分为深度和官渡两种,各有优缺点,就像人在追求卓越时,是着重深度还是看重广度,总是很难说的清除。
图的应用一共分为三种:最小生成树,最短路径和有向无环图的应用
最小生成树,我们讲了两种算法:普里姆(prim)算法和克鲁斯卡尔(Kruskal)算法。普里姆算法像是走一步看一步的思维方式,逐步生成最小生成树。而克鲁斯卡尔算法则是更有全局意识,直接从图中最短权值的边入手,找寻最后的答案。
最短路径的现实应用非常多,我们也介绍了两种算法。迪杰斯特拉(Dijkstra)算法更强调单源顶点查找路径的方式,比较符合我们正常的思路,容易理解原理,但算法代码相对复杂。而弗洛伊德(Floyd)算法则完全抛开了单点的局限思维方式,巧妙的应用矩阵的变换,用最清爽的代码实现了多顶点间最短路径求解的方案,原理理解有难度,但算法编写简洁。
有向无环图时常应用于工程规划中,对于整个工程或相同来说,我们一方面关心的是工程能否顺利进行的问题,通过拓扑排序的方式,我们可以有效的分析出一个有向图是否存在环,如果不存在,那他的拓扑序列是什么?另一方面关心的是整个工程完成所必须的最短时间问题,利用求关键路径的算法,可以得到最短完成工程的工期及关键的活动有哪些。