树是一种在实际编程中经常遇到的数据结构。他的逻辑很简单:除了根接待你之外每个节点中有一个父节点,根节点没有父节点;除了叶节点之外所有节点都有一个或多个子节点,叶节点没有子节点。父节点和子节点之间用指针链接。
二叉树的遍历方式:
前序遍历:先访问根节点,再访问左子节点,最后访问右子节点。
下图的前序遍历顺序是10,6,4,8,14,12,16.
中序遍历:先访问左子节点,再访问根节点,最后访问右子节点。
下图的遍历顺序是4、6、8、10、12、14、16.
后序遍历:先访问左子节点,再访问右子节点,最后访问根节点。
下图的遍历顺序是4、8、6、12、16、14、10.

这三种遍历都有递归和循环两种不同的实现方法,每一种遍历的递归实现都比循环实现简捷很多。
二叉树的另外两个特例是堆和红黑树。堆分为最大堆和最小堆。在最大堆中根节点的值最大,在最小堆中根节点的值最小。有很多需要快速找到最大值或者最小值的问题可以用堆来解决。红黑树是把树中的节点定义为红、黑两种颜色,并通过规则确保从根节点到叶节点的最长路径的长度不超过最短路径的两倍。
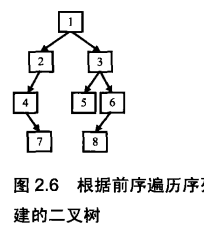
题目:输入二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},重建二叉树。
解题思路:在二叉树的前序遍历序列中,第一个数字总是树的根节点的值。但在终须遍历序列中,根节点的值在序列的中间,左子树的节点的值位于根节点的值的左边,而右子树的节点的值位于根节点的值的右边。因此我们需要扫面中序遍历序列,才能找到根节点的值。
如图,前序遍历序列的第一个数字就是根节点的值。扫描中序遍历序列,就能确定根节点的值的位置。根据中序遍历特点,在根节点的值1前面的3个数字都是左子树接待你的值,位于1后面的数字都是右子树节点的值