题意:
给出一个n*m的矩形,然后有两个操作.
1操作,对一个给出的菱形,对菱形范围内的东西进行+1。
2操作,对一个上半菱形的区域,进行+1操作。
最后求矩形内各个数的异或和。
思路:
在矩形中,我们在四个角上进行++--,然后利用差分的性质,就解决了区间更新,
但是在这里,想破脑汁,也没想出怎么进行++--。因为矩形的差分是横着或者竖着的,
最后的求和非常容易,但是这里不一样。最后看了题解豁然大悟,原来差分还可以动态的来,
本行的差分数组使用完了,还可以把差分数组下传,继续在下一层继续起到作用,这是神奇的操作。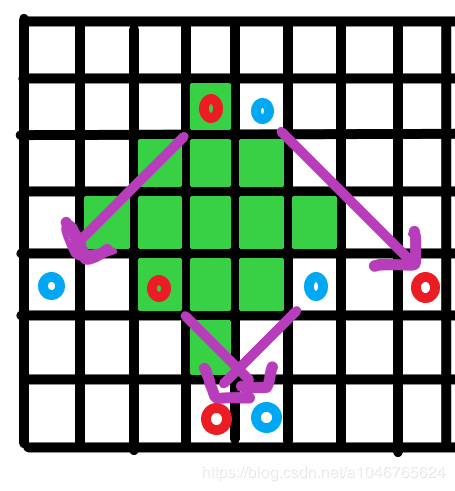
代码:

#include<bits/stdc++.h> using namespace std; typedef long long ll; #define N 3005 #define L 1000 int n,m,q; int a[N][N],b[N][N],c[N][N],d[N][N]; int bb[N][N]; void up(int x,int y,int l) { a[x-l/2][y]++;a[x+1][y-l/2-1]--; b[x-l/2][y+1]--;b[x+1][y+l/2+2]++; } void down(int x,int y,int l) { c[x+1][y-l/2+1]++;c[x+l/2+1][y+1]--; d[x+1][y+l/2]--;d[x+l/2+1][y]++; } int main() { while(~scanf("%d %d %d",&n,&m,&q)) { /*memset(a,0,sizeof(a)); memset(b,0,sizeof(a)); memset(c,0,sizeof(a)); memset(d,0,sizeof(a));*/ while(q--) { int op; int x,y,l; scanf("%d %d %d %d",&op,&x,&y,&l); x+=L,y+=L; up(x,y,l); if(op==1) down(x,y,l); } int ans=0; for(int i=0;i<n+2*L;i++) { int cnt=0; for(int j=0;j<m+2*L;j++) { cnt+=a[i][j]+b[i][j]+c[i][j]+d[i][j]; if(i>=L+1&&i<=L+n&&j>=L+1&&j<=m+L){ ans^=cnt;//bb[i-L][j-L]=cnt; } a[i+1][j-1]+=a[i][j]; b[i+1][j+1]+=b[i][j]; c[i+1][j+1]+=c[i][j]; d[i+1][j-1]+=d[i][j]; } } /* for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { cout<<bb[i][j]<<" "; } cout<<endl; }*/ printf("%d ",ans); } return 0; }
参考:https://blog.csdn.net/qq_41289920/article/details/86683583
