在semi-static环境下,slam地图的复用。
related works: 存储多个地图,哪个和观测匹配用哪个。
semi-static environment: The principal challenges with semi-static environments are the need to detect a change in the environment and update an existing map so that it reflects the most current state of the world. 地图上物体的移动导致地图不能被复用,需要检测到这些变化并重新更新地图
状态vector: $X = [x_p, x_l]$, $x_p$是所有的位姿,$x_l$是所有的landmark,也就是map里面的地图点feature。
观测vector: $Z$,所有的观测
优化目标(最大后验):$p( X | Z )$
data association vector $J$:所有data association的可能性,这个东西的定义,还没搞清楚,
是不是对每一次观测到的点xx找到对应的地图featureyy。
优化目标:$arg max_J p( J | Z)$:找到一个最优的J,使得条件概率p(J | Z)最大,也就是在Z观测下发生J的可能性最大。
已有方法:The usual solution is to solve for data associations with a search over possible associations, using techniques such as Joint Compatibility Branch and Bound (JCBB) [1] and then condition the state estimate on data associations: p(X |Z, J) where J is the vector of data associations that assign a feature in the state vector to a measurement. 会先用search的方法找一个J,然后基于Z和J优化X;但是在非static环境的假设下,找出的J应该有问题吧。
为了让每个feature有消失(被移动)的可能性,给它一个属性$Theta^t = {0,1}$,来表示一个feature在t时刻是否还存在。
顺序: 作者先用类似JCBB的方法计算一个J,在J的基础上预测$Theta^t$,最后预测$X$
feature $i = 1:M$
时刻 $t = 1:N$
survival time $T_i > 0$
persistance variable $Theta^t_i = 1 if T_i > t else 0$
$T_i ~ p_{T_i}()$ 没看懂,说是表示先验啥的,可能是Ti的先验分布吧
作者想计算feature $i$ 的persistance variable的边缘概率。也就是$p(Theta^t_i = 1 | J^{1:N})$,这里应该重新定义了J,之前说J是data assoication的集合,现在$J^{1:N}$ 代表了到时刻N为止所有feature被检测到的情况。$J^{1:N} = { J^{1:N}_1, J^{1:N}_2,... J^{1:N}_M }$,对于M个feature来说,$J^{1:N}_k = { j_k^{t_i}}_{i=1}^N, j = 0,1$
看到这里,似乎有一个假设是,地图里已保存有M个feature是确定了的。
We are interested in estimating the full joint feature persistence posterior at a certain time t, given all data association decisions from time t1 to tN:
$p(Theta^t = 1 | J^{1:N})$
$ Theta^t riangleq {Theta^t_1,...Theta^t_M }, t > t_N$
在这里产生了疑问,J到底是什么,按后面的定义detection,只是feature有没有被检测到,0,1变量,但是前面提到的data association,觉得似乎是把一个观测值和一个feature联系起来的过程,是个one-hot之类的东西,肯定不止0,1的信息量, 当然有了association, 0,1的值也就有了。这个公式里还是比较倾向于0,1的定义,因为没有涉及到任何观测Z。
It is important to note that we only estimate the persistence probability for times equal to or greater than the last received measurement tN.
根据上面的公式等价一下,$p(Theta^t = 1 | J^{1:N}) = p(T > t | J^{1:N})$, $T riangleq { T_i}_{i=1}^N $
那么根据贝叶斯定理优化最大的最大后验
$p(Theta^t = 1 | J^{1:N}) = frac { p(J^{1:N} | T>t) p(T > t) } {p(J^{1:N})}$
作者对公式右边的项找近似。
这段公式不想打了,啊啊啊,我还是没有懂,$Theta$ 和 $T$ 到底是个什么东西,是个集合吗,$T > t$到底代表了什么,T里面有这么多元素, 好像就是作者自己设计的一种联合表达,然后自己提出独立的假设把它分解开来。我就觉得用T这个集合没有实际物理意义啊,反正底下都乘法分解了。

上面的公式经过分解成了两个连乘,最后的子项变成,
我们仍然需要计算概率$p( j_i^t | T_i)$ which is the probability of detecting a feature given its survival time Ti.
根据data association的不完美特性,
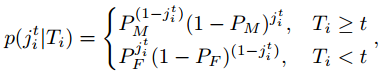
PM是存在但是误检的概率,PF是不存在但是假警的概率。We present PM and PF as constants, but they could be modified per observation, e.g., to include occlusions.
The core contribution of this work is in the modeling and evaluation of p(Θt), the joint prior distribution over feature persistence (at time t).
核心贡献是计算$p(T > t)$.
$p( T > t) = prod_{i=1}^M p(T_i > t)$这个公式会假设所有的点独立,但是实际上很多点有相关。
在很多环境里,一个feature的存在明显与另一个feature相关,但是计算一个full joint distribution P(T>t)的复杂度是$2^M$,如果存在M个特征点。所以我们考虑引入一些structure,比如可以认为一个物体是一个structure, 一个segment是一个structure都可以。计算的上限就变成了$2^L$如果有L个structure.
假设有L个structure组成的集合$ { au_i }_{i=1}^L, L < M$. 联合概率的公式就变成
$p( T > t) = prod_{i=1}^L p( au_i^t )$
下图的公式等下再解释,

公式八似乎是核心,但是完全没看懂在干什么,可能公式7那里就lost了。

公式9还没看懂
先跳过一些章节,看一下evaluation
分别做了仿真和实际数据测试。
把2d map里面的一些路标点进行移动,移动之后防止错误的data association, 如果一个点被检测为不存在,那么它对应的所有的clutter里面的点都会被
认为不存在,进行feature removal。物体移动的范围也有个2,3米,还是挺大的,其实移动的越大,越能检测出地图出问题了,那么就直接remove这些地图点。
读到这里突然明白paper的功能了,地图里有环境变化,一个地图点的移动(本文只涉及这一种变化),如果强行的让算法去做data association, 很有可能会让数据关联错,关联错了的结果就是定位错误。
要怎么知道某个时刻发生的是,物体点移动还是观测到错误数据呢,作者最后给了一个举例。例如,如果一系列连续的和共线的车道标记由点特征表示,并且在持久性上具有相关联的联合先验分布,并且这些车道标记已经发生了微小的变化,则假定在某个点上车辆位置的姿态不确定性为足够小,我们可以确定该组中至少没有一个功能;那么即使姿态不确定性增加并且我们无法单独确定组中的每个特征都不再存在,联合持久性模型也可以让我们推断其他车道标记的不存在,例如:图2
只要能持续的更新persistence,那么一个点的persistence降低,似乎会影响到它的整个clutter。
怎么样确定一个时刻位姿不确定性呢,不知道,做orbslam的过程里似乎没有这个变量啊。